


















Проектирование ступенчатой колонны
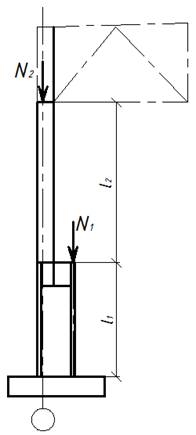 Требуется подобрать сечения
сплошной верхней и сквозной нижней частей колонны (сопряжение ригеля с колонной
– жесткое).
Требуется подобрать сечения
сплошной верхней и сквозной нижней частей колонны (сопряжение ригеля с колонной
– жесткое).
Для верхней части колонны в сечении 4–4:
![]() ,
,
![]() .
.
Для нижней части колонны:
![]() ,
,
![]() (догружается
наружная ветвь);
(догружается
наружная ветвь);
![]() ,
,
![]() (догружается
подкрановая ветвь).
(догружается
подкрановая ветвь).
|
Определение расчетных длин колонны
Расчетные длины в плоскости рамы:
![]() ,
,
![]() , где
, где ![]() ,
,
![]() –
коэффициенты расчетной длины нижней и верхней частей колонны соответственно;
–
коэффициенты расчетной длины нижней и верхней частей колонны соответственно;
![]() ,
,
![]() –
геометрические длины нижней и верхней частей колонны.
–
геометрические длины нижней и верхней частей колонны.
 Коэффициент для верхней части колонны
Коэффициент для верхней части колонны
![]() , где
, где
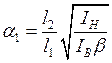 , где
, где
![]() ,
,
|
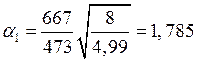 .
.
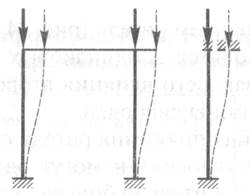
Для определения ![]() , следует
рассмотреть условия закрепления концов колонны. Нижний конец принимается
защемленным, верхний – закреплен только от поворота (жесткое сопряжение ригеля
с колонной, жесткость ригеля значительно больше жесткости колонны).
, следует
рассмотреть условия закрепления концов колонны. Нижний конец принимается
защемленным, верхний – закреплен только от поворота (жесткое сопряжение ригеля
с колонной, жесткость ригеля значительно больше жесткости колонны).
По прил. 6 [1] ![]() зависит от
величин
зависит от
величин ![]() и
и ![]() (табл. 68 [1]).
(табл. 68 [1]).
![]() Þ
Þ ![]() .
.
Тогда
![]() .
.
Расчетные длины в плоскости рамы:
![]() ;
;
![]() .
.
Расчетные длины из плоскости рамы:
![]() ;
;
![]() .
.
Подбор сечения верхней части колонны.
Сечение принимаем в виде сварного двутавра высотой ![]() .
.
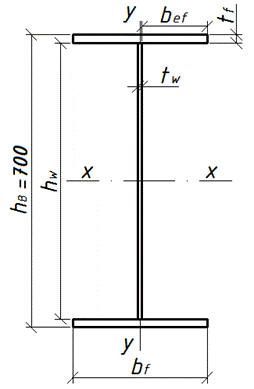 Требуемая площадь:
Требуемая площадь:
![]() .
.
Для симметричного двутавра предварительно принимаем величины:
![]() ,
,
![]() .
.
Тогда условная гибкость стержня:
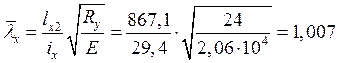 .
.
Приведенный эксцентриситет
![]() ,
,
|
![]() –
коэффициент влияния формы сечения, принимается по табл. 73 [1], зависит
от отношения
–
коэффициент влияния формы сечения, принимается по табл. 73 [1], зависит
от отношения ![]() (предварительно
принимаем
(предварительно
принимаем ![]() ), условной
гибкости
), условной
гибкости ![]() и
относительного эксцентриситета
и
относительного эксцентриситета ![]() .
.
Принимаем ![]() .
.
Получим ![]() .
.
Далее, по прил. 9 [3] при ![]() и
и ![]() Þ
Þ ![]() .
.
Тогда ![]() .
.
Требуемая площадь сечения велика, прокатный двутавр подобрать не получится, поэтому приходится компоновать сечение из трех листов.
Приступаем к компоновке сечения. Высота стенки:
![]() , где предварительно
, где предварительно ![]() .
.
Предельная гибкость стенки (при ![]() и
и ![]() ):
):
![]() .
.
Требуемая толщина стенки:
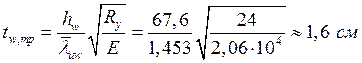 ,
,
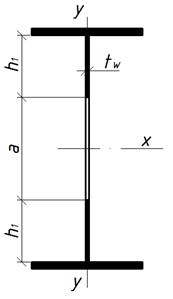 но сечение с такой толстой
стенкой неэкономично, принимаем
но сечение с такой толстой
стенкой неэкономично, принимаем ![]() (
(![]() ).
).
Поскольку переход стенки в критическое состояние еще
не означает потерю несущей способности стержня, по СНиП допускается
использование закритической работы стенки. В этом случае неустойчивую часть
стенки (размер а) считают выключившейся из работы, а в расчетную площадь
сечения колонны включаем только устойчивую часть стенки, т.е. два участка
шириной ![]() ,
примыкающие к полкам (рис. 5.4).
,
примыкающие к полкам (рис. 5.4).
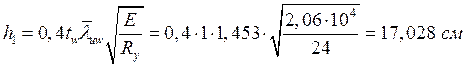 .
.
|
![]() .
.
Принимаем ![]() ,
т.к.
,
т.к. 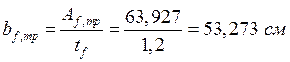 .
.
Фактическая площадь полки![]() .
.
Устойчивость полки обеспечена, если выполняется следующее условие:
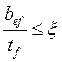 , где
, где ![]() –
отношение ширины свеса к толщине, для неокаймленной полки двутавра и тавра:
–
отношение ширины свеса к толщине, для неокаймленной полки двутавра и тавра:
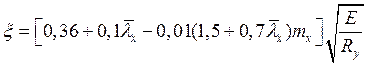
![]()
 .
.
Условие не выполняется, назначаем другие размеры сечения.
Для обеспечения устойчивости колонны из плоскости
действия момента ширина полки принимается не менее ![]() .
.
Толщина полки ![]() , толщина
стенки
, толщина
стенки ![]() , тогда
высота стенки:
, тогда
высота стенки:
![]() .
.
Устойчивая часть стенки ![]() , требуемая
площадь полки
, требуемая
площадь полки ![]() .
.
Принимаем ![]() ,
т.к.
,
т.к. 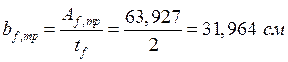 .
.
Фактическая площадь полки ![]() .
.
Устойчивость обеспечена, т.к. выполняется условие:
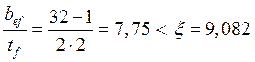 .
.
Фактические геометрические характеристики скомпонованного сечения.
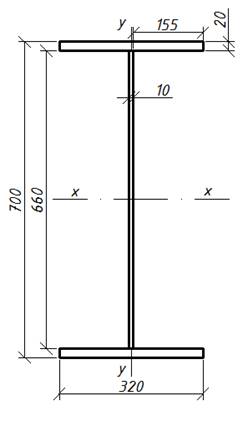 Общая площадь сечения:
Общая площадь сечения:
![]() .
.
Моменты инерции относительно главных осей:
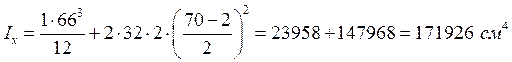 ,
,
![]() .
.
Радиусы инерции сечения:
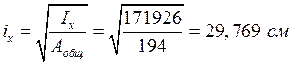 ,
,
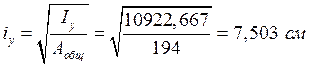 .
.
Момент сопротивления:
|
радиус ядра сечения:
![]() .
.
Гибкость и условная гибкость стержня:
![]() ,
,
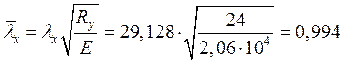 ,
,
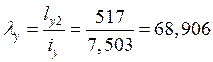 ,
,
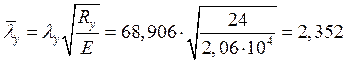 .
.
Предельная условная гибкость стенки:
![]() .
.
Устойчивая часть стенки:
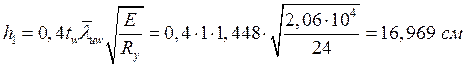 .
.
Площадь сечения с учетом выключения из работы неустойчивой части стенки:
![]() .
.
Проверка устойчивости в плоскости действия момента:
![]() .
.
Для определения ![]() найдем
следующие величины:
найдем
следующие величины:
относительный эксцентриситет ![]() , отношение площади полки к площади стенки
, отношение площади полки к площади стенки ![]() .
.
По табл. 73 [1] принимаем:
![]() .
.
Тогда ![]() Þ
Þ ![]() .
.
Проверка устойчивости:
![]()
Условие выполнено.
Проверка устойчивости из плоскости действия момента:
![]()
Коэффициент продольного изгиба по прил. 8 [3] при ![]() Þ
Þ ![]() .
.
Для определения ![]() найдем максимальный
момент в средней трети длины стержня при том же сочетании нагрузок, которое
было принято для расчета верхней части колонны (1, 2, 3, –5, 8). Момент
в сечении 3–3 при этом сочетании нагрузок (
найдем максимальный
момент в средней трети длины стержня при том же сочетании нагрузок, которое
было принято для расчета верхней части колонны (1, 2, 3, –5, 8). Момент
в сечении 3–3 при этом сочетании нагрузок (![]() ):
): ![]() .
.
Получаем максимальный момент в средней трети: ![]() .
.
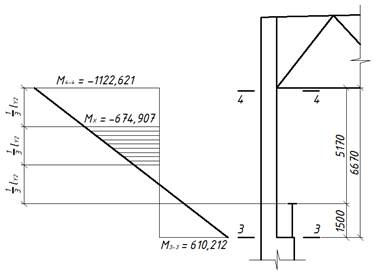
![]() , (не менее
половины наибольшего по длине стержня момента).
, (не менее
половины наибольшего по длине стержня момента).
Относительный эксцентриситет ![]() .
.
При ![]() ,
,
![]() , где
, где ![]() –
коэффициент, учитывающий влияние момента
–
коэффициент, учитывающий влияние момента ![]() при
изгибно-крутильной форме потери устойчивости;
при
изгибно-крутильной форме потери устойчивости;
![]() ,
,
![]() ,
, ![]() –
коэффициенты, определяемые по прил. 12 [3]:
–
коэффициенты, определяемые по прил. 12 [3]:
|
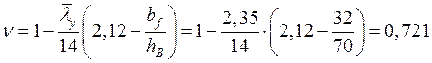 .
.
Тогда ![]() .
.
Проверка устойчивости:
![]() .
.
Условие выполнено.
Подбор сечения нижней части колонны.
Принимаем сечение из двух ветвей, связанных между собой соединительной решеткой.
Высота сечения ![]() . Принимаем
предварительно
. Принимаем
предварительно ![]() ,
, ![]() .
.
|
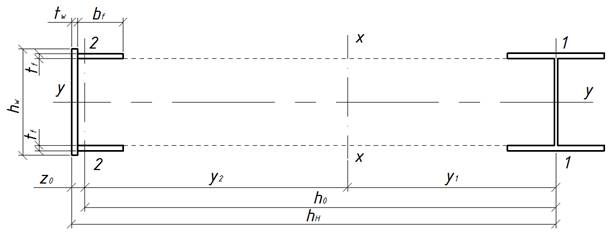
Ориентировочное положение центра тяжести всего сечения:
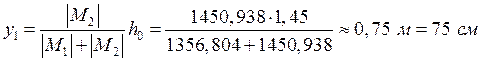 ,
,
![]() .
.
Усилия в ветвях:
для подкрановой ![]() , для наружной
, для наружной ![]() .
.
Задаемся ![]() .
Тогда требуемая площадь ветвей:
.
Тогда требуемая площадь ветвей:
для подкрановой ![]() , для наружной
, для наружной ![]() .
.
По сортаменту принимаем колонный двутавр I 30К3:
![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Для наружной ветви принимаем сварной швеллер из трех
листов, просвет между внутренними гранями полок принимаем таким же, как в подкрановой
ветви, для удобства крепления решетки (269
мм). Толщину стенки ![]() –
для удобства соединения встык с полками верхней части колонны, ширину стенки,
из условия размещения сварных швов –
–
для удобства соединения встык с полками верхней части колонны, ширину стенки,
из условия размещения сварных швов – ![]() .
.
Требуемая площадь полок ![]() , принимаем размеры
, принимаем размеры ![]() и
и ![]() .
.
Из условия местной устойчивости полок проверяем 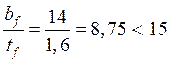 .
.
Геометрические характеристики наружной ветви.
Площадь сечения: ![]() .
.
Расстояние от внешней грани стенки до центра тяжести:
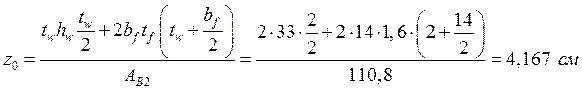 ,
,
Моменты инерции и радиусы инерции:
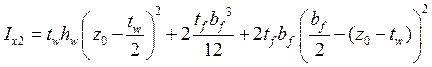 ,
,
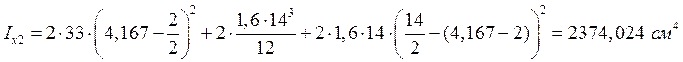 ;
;
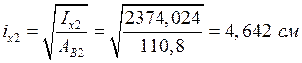 ;
;
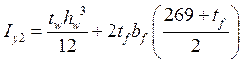 ,
,
![]() ;
;
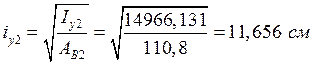 .
.
Уточняем положение центра тяжести всего сечения колонны:
![]() ,
,
![]() ,
,
![]() .
.
|
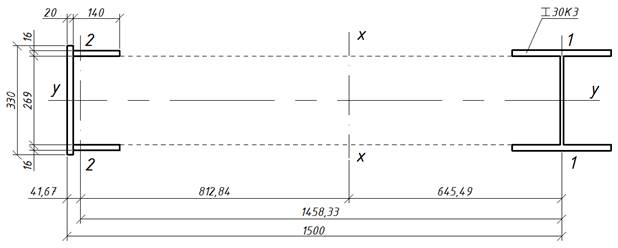
Получили существенное отличие от принятых первоначально размеров, поэтому пересчитываем усилия в ветвях:
![]() ,
,
![]() .
.
Проверка устойчивости ветвей.
Из плоскости рамы расчетная длина ![]() .
.
Для подкрановой ветви:
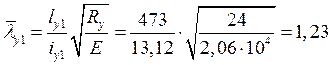 .
.
По прил. 8 [3]: ![]() .
.
Устойчивость обеспечена, т.к. выполняется условие:
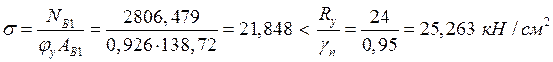 .
.
Для наружной ветви:
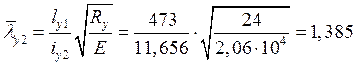 Þ
Þ ![]() .
.
Устойчивость также обеспечена из условия:
![]() .
.
Из условия равноустойчивости подкрановой ветви в плоскости и из плоскости рамы определяем требуемое расстояние между узлами решетки:
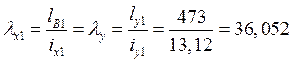 Þ
Þ ![]()
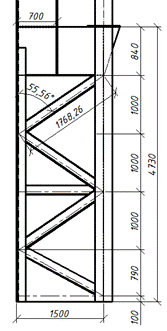 Принимаем
Принимаем ![]() .
.
Проверяем устойчивость ветвей в плоскости рамы
(относительно осей ![]() и
и
![]() ).
).
Для подкрановой ветви:
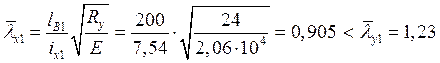 ,
устойчивость обеспечена.
,
устойчивость обеспечена.
Для наружной ветви:
|
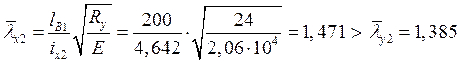 ,
устойчивость не обеспечивается, поэтому применяем стойки для уменьшения
расстояния между узлами наружной ветви,
,
устойчивость не обеспечивается, поэтому применяем стойки для уменьшения
расстояния между узлами наружной ветви, 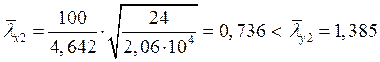 ,
устойчивость обеспечена.
,
устойчивость обеспечена.
Расчет решетки нижней части колонны.
Расчетная поперечная сила выбирается как большая из двух сочетаний, составляемых для поперечной силы в сечении 4–4:
![]() :
:
![]() ,
,
![]() :
:
![]() .
.
Принимаем для расчетов ![]() .
.
Условная поперечная сила для стали С245 может
быть принята по табл. 8.2 [3]: ![]()
Расчет решетки производим по ![]() . Усилия
сжатия в раскосе:
. Усилия
сжатия в раскосе:
![]() , где
, где ![]() –
угол между вертикалью и осью раскоса.
–
угол между вертикалью и осью раскоса.
Задаемся ![]() ,
тогда
,
тогда
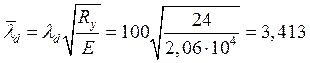 .
.
По прил. 8 [3]: ![]() .
.
Необходимая площадь сечения раскоса:
![]() , где
, где ![]() –
при использовании уголка, прикрепленного одной полкой
–
при использовании уголка, прикрепленного одной полкой
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.