Основы дискретной математики

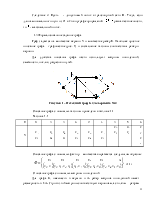
Циклическое число определяется только для неориентированных графов. По варианту, дан ориентированный граф, то циклическое число находить не нужно.

1.8 Вершинное и реберное числа независимости

Множество SV графа G = (V, Г) называют внутренне устойчивым, если никакие две вершины из S не смежны, т.е. для любого хS имеет место ГхS¹Æ.

Множество внутренней устойчивости, содержащее наибольшее число элементов, называют наибольшим внутренне устойчивым множеством, а число элементов этого множества – числом внутренней устойчивости e₀(G) графа G (это число называют также вершинным числом независимости графа).

Два ребра графа называют смежными, если они инцидентны одной и той же вершине. Максимальное число попарно несмежных ребер графа называется его реберным числом независимости e₁(G).

Вершинное и реберное числа независимости графа на рисунке 1

e₀(G)=2       

e₁(G)=3        

1.9 Числа вершинного и реберного покрытий графа

Если ребро графа инцидентно его вершине, то говорят, что они покрывают друг друга. Множество вершин, покрывающих все ребра графа, называют вершинным покрытием графа G, а минимальную мощность этого множества - числом вершинного покрытия графа p₀(G). Аналогично, множество ребер, покрывающих все вершины графа, называют реберным покрытием графа G, а минимальную мощность этого множества – числом реберного покрытия графа p₁(G).

Числа вершинного и реберного покрытий графа на рисунке 1:

p₀(G)=4         

p₁(G)=5        

1.10 Вершинное и реберное число внешней устойчивости графа

Множество ТÌV графа G=(V, Г) называют внешне устойчивым, если любая вершина, не принадлежащая Т, соединена ребрами с вершинами из Т, т.е. для любого хÏТ имеет место ГхÇТ¹Æ.

Множество внешней устойчивости, содержащее наименьшее число элементов, называется наименьшим внешне устойчивым множеством, а число элементов этого множества – вершинным числом внешней устойчивости b₀(G) графа G.

Минимальная мощность множества ребер, покрывающих все ребра графа, называется реберным числом внешней устойчивости b₁(G) графа G.

Вершинное и реберное числа внешней устойчивости графа на рис.1.1:

b₀(G)= 2       

b₁(G)= 2       

2 СИНТЕЗ ЛОГИЧЕСКИХ СХЕМ

Синтез логических схем осуществляется на основе заданной функции алгебры логики. Функция, определенная на наборах <x_n-1, …, x_i, …, x₂, x₁, x₀> и принимающая на этих наборах значение 0 или 1, называется функцией алгебры логики.

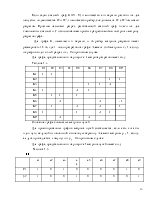
2.1 Таблица истинности функции алгебры логики          

    - (1)               

2.2 Совершенные дизъюнктивная и конъюнктивная  нормальные формы

СДНФ:

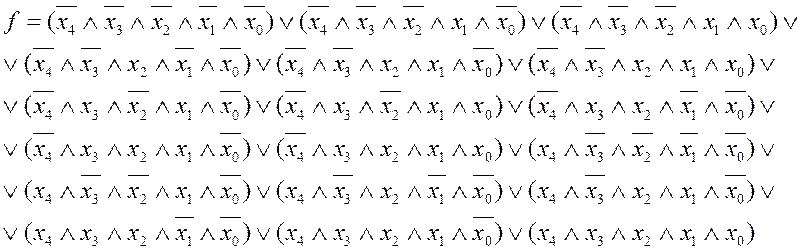Сложность формулы  a(Y)=5*18=90

СКНФ:

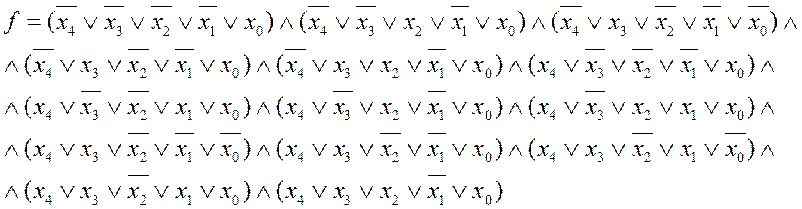Сложность формулы  a(Y)=5*14=60

2.3 Анализ функции алгебры логики на принадлежность к классам

Так как f(0, 0, 0, 0, 0) = 1, то данная функция алгебры логики не принадлежит к классу функций сохраняющих ноль, т.е. fÏK₀

Так как f(1, 1, 1, 1, 1)=0, то данная функция алгебры логики принадлежит к классу функций сохраняющих единицу, т.е. fÏK₁

Анализ функции алгебры логики на принадлежность к классу линейных функций:

f_л=CÅC₀x₀ÅC₁x₁ÅC₂x₂ÅC₃x₃ÅC₄x₄

Коэффициент С находим на наборе <0,0,0,0,0>

f(00000)= CÅ0Å0Å0Å0Å0=C=1, тогда C=1

Коэффициент С₄ находим на наборе <0,0,0,0,1>

f(00001)= 1Å0 Å0Å0Å0ÅC₄*1=1, тогда C₄=0

Коэффициент С₃ находим на наборе <0,0,0,1,0>

f(00010)= 1Å0Å0Å0ÅC₃*1Å0=0, тогда C₃=1

Коэффициент С₂ находим на наборе <0,0,1,0,0>

f(00100)= 1Å0Å0ÅC₂*1Å0Å0=1, тогда C₂=0

Коэффициент С₁ находим на наборе <0,1,0,0,0>

f(01000)= 1Å0ÅC₁*1Å0Å0Å0=1, тогда C₁=0

Коэффициент С₀ находим на наборе  <1,0,0,0,0>

f(10000)= 1ÅC₀*1Å0Å0Å0Å0=0, тогда C₀=1

f_л=1

Идет несовпадение, значит функция не линейная, т.е. fÏK_л.

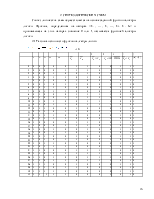
Анализ функции алгебры логики на принадлежность к K_с. Выразим обратную функцию (1) и составим таблицу истинности для обратной функции и сравним с исходной :

Анализируем полученную таблицу и приходим к выводу что функция не принадлежит к классу fÏ K_с.

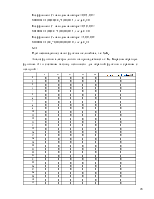
Проверим принадлежность функции алгебры логики к классу монотонных функций f_м:

Если в полученной матрице есть хотя бы один знак “-“, то функция не является монотонной, т.е. fÏ K_м

2.4 Минимизация функции алгебры логики

Для минимизации несложных функций применяются алгебраические преобразования на основе законов поглощения и склеивания. Для более сложных функций разработаны специальные методы минимизации такие как: Гарвардский метод, метод минимизирующих карт, метод Квайна - Мак–Класски.

2.5 Минимизация с помощью карт Карно

Продолжение карты Карно

Записываем МДНФ  в виде логической суммы конъюнкций, соответствующих выполненным накрытиям:

2.6 Минимизация методом Квайна -  Мак-Класски

Этот метод использует перебор конъюнкций, которые могут присутствовать