Не дивлячись на виконання умови теореми про вибірки, у обчисленому спектрі не виникне похибки, коли дискретизація має великий період або ціле число періодів.
Також відомо, що спектральна здатність, збільшується зі збільшенням часу спостереження.
Перед початком обчислень необхідно записувати значення вибірок в пам'ять, яка буде заповнена тим швидше, чим частіше будуть робитися вибірки, продовжуватиметься час спостереження, або чим більшою буде розрядність анолого-цифрового перетворювача (АЦП).
1.1 Реалізація ДПФ на ЕОМ
Для цього необхідно зображати часову і спектральну функції, як послідовності
(1.1.1)
(1.1.2)
де 
(1.1.3)
Тоді
(1.1.4)
Пряме обчислення спектру по цій формулі потребує N2 операцій комплексного множення і N (N-1) операцій комплексного додавання.
Машинний час в значній мірі пропорційний числу операцій множення. Тому навіть на ЕОМ ДПФ для великих послідовностей виконується досить довго.
Із структури рівнянь перетворення та
періодичності комплексної складової 
випливає багато можливостей по значному
скороченню часу обчислень. Такі алгоритми називаються швидким перетворенням
Фур'є (ШПФ). Вони дають такий самий результат при значно менших затратах.
1.2 Швидке перетворення Фур'є
Основна ідея ШПФ полягає в розгляді послідовності f(n) із N значень на декілька менших підмножин, які перетворюються потім окремо.
Це дуже ефективно коли N є стелінню по основі 2. Вхідна послідовність fn cпочатку ділиться на дві підмножини, елементи яких мають часовий інтервал 2Т. Ці підмножини в свою чергу також діляться навпіл і так до тих пір, поки в послідовності не залишаться два елементи, до яких застосовується ДПФ.
Проведемо результат розчеплення для N=8.
Вводять скорочення 
.
Звернення Fd(k) можна узагальнити так:
Оскільки 
і 
то множини 
в квадратних дужках для будь-яких 
мають значення 
. Тому на першому кроці обчислення пари 
уже готові.
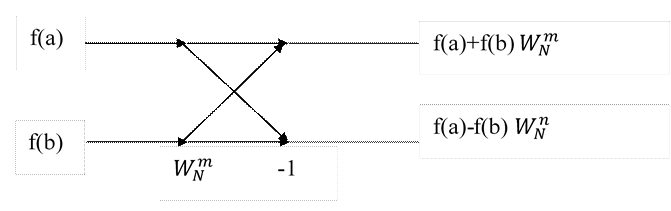
Рис.1.1 Основна операція ШПФ
Ця основна операція завжди повторюється.
Передбачуючи, що множини 
і 
для будь-яких k
повинні приймати значення 
, будуються комбінації з результатами першого
кроку. На наступних кроках спектральні лінії F(k) вираховуються уже із готових співмножників, а
також з допомогою основної операції.
Виконання алгоритму ШПФ можна реалізувати „ на одному місці ”. Вихідна послідовність поступово будується в пам'яті вихідного вектора. Для того щоб отримувати результати виді, вхідні дані повинні бути представлені в біт-зворотньому порядку.
Кількість операцій комплексного множення при обробці N вхідних даних по алгоритму ШПФ: вони розділяються на lg(N) кроків, на кожному з яких потрібно виконати N/2 основні операції ШПФ. Кожна така операція має одну операцію комплексного множення, то їх всього потрібно (N/2) lg(N). Це дає значний виграш в часі, в порівнянні з ДПФ.
2. ВИБІР ЕЛЕМЕНТНОЇ БАЗИ
При проектуванні пристроїв на МП необхідно сумісно розробляти програмні та апаратні засоби.
На основі поставленої задачі, та математичних методів її вирішення формуються вимоги до вибору типу мікропроцесора.
Так як використовуваний алгоритм вимагає виконання складних математичних операцій, то доцільно використати 16-ти розрядний мікропроцесор TMS320C52 фірми Texas Instruments.
Оскільки необхідно запам’ятовувати 2000 значення вибірок при 16-ти розрядній ША, то для побудови ОЗП вистачає потужностей самого процесора, у якому 9 К х16. Молодший банк даних буде запам’ятовуватися в D-0 – D7, для парних адрес та D-8 – D-15 для непарних.
Важливим є вибір АЦП, найкраще всім вимогам технічного завдання та вибраному МП відповідає 12-ти розрядний АЦП ADC78H90, на його вхід можна подавати сигнали амплітудою 5,5 В. Тому необхідно використати подільник на 2 з частотною компенсацією.
3. ВИБІР СТРУКТУРНОЇ СХЕМИ
Робота пристрою починається з того, що за допомогою сигналів МRDC та А15 читається перша команда з ПЗП по нульовому адресу. Всі наступні дії пристрою стають незалежними від програми.
Блок схема яка описує роботу пристрою в цілому.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.