Рекуррентные формулы. Рекурсивные алгоритмы и подпрограммы

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»

Факультет физико-математических и компьютерных наук

Кафедра прикладной математики и информационных технологий

Специальность 010500 – «Информационные системы и технологии»

Курсовая работа

по дисциплине “Языки и методы программирования”

на тему:

Рекуррентные формулы. Рекурсивные алгоритмы и подпрограммы

Выполнила:

студентка 1 курса

группы ИС-1

________________________

(подпись студента)

_____________________________________

(оценка)

Научный руководитель:

к.т.н., доцент

________________________

(подпись преподавателя)

Липецк 2012

Оглавление

ВВЕДЕНИЕ.. 4

ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРИМЕНЕНИЯ РЕКУРСИИ В ПРОГРАММИРОВАНИИ.. 6

1.1.     Рекуррентные формулы в математике. 6

1.2.     Рекурсивные алгоритмы и подпрограммы.. 9

1.3.     Примеры рекурсивных программ.. 11

1.3.1.        Рекурсия и итерация. 11

1.3.2.        Стек. 13

1.3.3.        Сложность рекурсивных вычислений.. 14

1.3.4.        Метод «разделяй и властвуй». 15

1.3.5.        Динамическое программирование. 16

ГЛАВА 2. РЕКУРСИЯ В СРЕДЕ ПРОГРАММИРОВАНИЯ DELPHI. 18

2.1.     Организация рекурсивных процедур и функций в Delphi 18

2.2.     Примеры рекурсивных алгоритмов, процедур и функций. 20

2.2.1.          Поиск элемента в упорядоченном массиве (двоичный поиск) 20

2.2.2.          Ханойские башни.. 21

2.2.3.          Размен денег. 23

2.2.4.          Размен денег 2. 24

2.2.5.          Вычисление суммы элементов линейного массива.. 26

2.3.     Рекурсивное определение наибольшего общего делителя двух натуральных чисел на основе алгоритма Евклида. 27

2.3.1.          Реализация Pascal в рекурсивном виде. 27

2.4.     Рекурсивное  нахождение чисел Фибоначчи, принадлежащих указанному диапазону значений. . 28

2.4.1.          Реализация Pascal в рекурсивном виде. 29

2.5.     Рекурсивное определение геометрической прогрессии. 30

2.5.1.          Реализация Pascal в рекурсивном виде. 30

2.6.     Построение правильного многоугольника. 32

2.7.     Построение окружностей. 35

ЗАКЛЮЧЕНИЕ.. 38

СПИСОК ЛИТЕРАТУРЫ... 39

ВВЕДЕНИЕ

Полезность, важность и необходимость рекурсии, как одного из концептуальных методов решения практических задач известна всем программистам.

Американский специалиста по системному программированию Д.Кнут, например, широко использовал рекурсию при изложении материала в ставшем уже классическим трехтомнике “Искусство программирования для ЭВМ”. Английскому теоретику информатики Ч.Хоару принадлежат следующие слова “Следует отдать должное гению разработчиков Алгола-60 за то, что они включили в свой язык рекурсию и дали мне тем самым возможность весьма элегантно описать мое изобретение (речь идет о так называемой быстрой сортировке Хоара – Quick Sort). Сделать возможным изящное выражение хороших мыслей – я считал это наивысшей целью проекта языка программирования”. На сегодняшний день, практически все действующие языки программирования поддерживают рекурсию.

Цель курсовой работы знакомство с применением рекурсии в программировании.

Задачи работы:

1)  проанализировать научно-методическую литературу по теме исследования;

2)  познакомиться с понятиями рекуррентных формул в математике, рекурсивных алгоритмов и подпрограмм;

3)  проанализировать некоторые распространенные рекурсивные алгоритмы;

4)  освоить возможности среды  Delphi по организации рекурсивных процедур и функций;

5)  разработать примеры рекурсивных алгоритмов, процедур и функций.

В курсовой работе дается неформальное понятие рекурсии, рассказывается об общей схеме решения задач с помощью рекурсии и приведены рекурсивные алгоритмы решения весьма разнообразных по содержанию и степени сложности задач.

ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПРИМЕНЕНИЯ РЕКУРСИИ В ПРОГРАММИРОВАНИИ

1.1. Рекуррентные формулы в математике

Рекуррентным соотношение, рекуррентным уравнением или рекуррентной формулой  называется соотношение вида  , которое позволяет вычислять все члены последовательности  , если заданы ее первые  членов.

Примеры.

1.  Формула  задает арифметическую прогрессию.

2.  Формула  определяет геометрическую прогрессию.

3.   Формула  задает последовательность чисел Фибоначчи.

В случае, когда рекуррентное соотношение линейно и однородно, т.е. выполняется соотношение вида:

 (1)

(), последовательность  называется возвратной.

Многочлен

 (2)

называется характеристическим для возвратной последовательности {.

Корни многочлена  называются характеристическими.

Множество всех последовательностей, удовлетворяющих данному рекуррентному соотношению, называется общим решением.

Описание общего решения (1) имеет аналоги с описание решения обыкновенного дифференциального уравнения с постоянными коэффициентами.

Теорема 1. 1.Пусть λ – корень характеристического многочлена (2). Тогда последовательность {с}, где с – произвольная константа, удовлетворяет соотношению (1).

2. Если,- простые корни характеристического многочлена (2), то общее решение рекуррентного соотношения (1) имеет вид  , где ,  , … , - произвольные константы.

3. Если  - корень кратности  () характеристического многочлена (2), то общее решение рекуррентного соотношения (1) имеет вид

,

где  - произвольные константы.

Зная общее решение рекуррентного уравнения (1), по начальным условиям  можно найти неопределенные постоянные  и тем самым получить решение уравнения (1) с данными начальными условиями.

Пример 1.Найти последовательность {}, удовлетворяющую рекуррентному соотношению  и начальным условиям

Корнями характеристического многочлена  являются числа . Следовательно, по теореме 1 общее решение имеет вид . Используя начальные условия, получаем систему

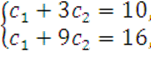
Решая которую, находим  Таким образом, .

Рассмотрим неоднородное линейное рекуррентное уравнение

    (3)

Пусть  {} – общее решение однородного уравнения (1), а {} – частное (конкретное) решение неоднородного уравнения (3). Тогда последовательность  {} j, образует общее решение уравнения