Федеральное агентство связи
Государственное образовательное учреждение высшего профессионального образования
Сибирский Государственный Университет Телекоммуникаций и Информатики
Кафедра ТЭЦ
Курсовая работа по ОТЦ
Тема: Расчет электрических цепей при импульсном воздействии
Выполнила:
Группа А-43
Проверила:
Новосибирск, 2006
Содержание.
1.Введение……………………………………………………………………..3
2. Задание …………………………………………………………………………………...3
3.Вычисление напряжения на выходе цепи………………………………3
3.1.Переходная характеристика цепи…………………………………...4
3.2 Анализ входного сигнала……………………………………………………..4
3.3.Запишем интеграл Дюамеля для каждого интервала цепи……….5
3.4. Напряжение на выходе………………………………………………5
4.Вычисление спектра сигнала на выходе цепи U2(jω)………6
4.1Спектральная плотность входного сигнала………………………..6
4.2 AЧX и ФЧХ передаточной функции цепи………………………....9
4.3 Импульсная характеристика цепи………………………………….10
4.4 Импульсная характеристика цепи………………………………….12
5. Дискретизация входного, выходного сигнала и импульсной характеристики цепи………………………………………………………..12
5.1 Дискретизация входного сигнала…………………………………12
5.2 Дискретизация импульсной характеристики…………………….13
5.3 Дискретизация выходного сигнала ……………………………….13
6. Спектральные характеристики дискретизированного сигнала…………………15
7. Z – преобразование импульсной характеристики цепи…………………………16
8. АЧХ дискретной цепи……………………………………………………………..17
9. H-корректора……………………………………………………………………….18
10. АЧХ корректирующей цепи……………………………………………………...21
11. Вывод………………………………………………………………………………23
1.Введение
Цель курсовой работы состоит в систематизации и закреплении знаний, полученных студентами при изучении классического, операторного и спектрального методов, расчета процессов в линейны электрических цепях, а также теоретических основ анализа дискретных сигналов и линейных дискретных систем.
2. Задание
Задание на курсовую работу содержит схему анализируемой цепи( Рис. 1) и входной сигнал в виде одиночного импульса(Рис. 2), параметры которого указаны на рисунке. Все резисторы схемы имеют сопротивление R=1 КОм, индуктивность катушек L=1Гн, емкость конденсаторов С = 1мкФ.
R
R L R U2
U1
Рис 1. Схема цепи.
R=1 кОм = 1000 Ом;
L=1 Гн;
C=1 мкФ = 0.00001 Ф.
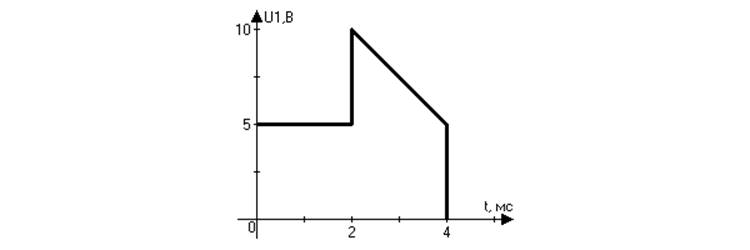
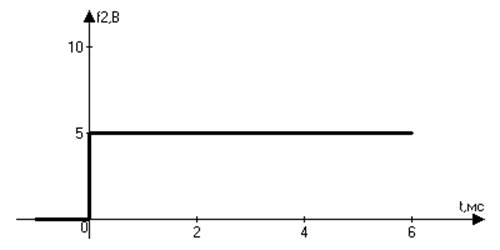
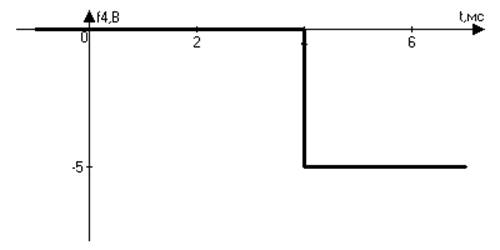
Рис.2 График зависимости входного сигнала от времени.
3.Вычисление напряжения на выходе цепи.
Необходимо получить аналитические выражения, описывающие u2(t) на различных интервалах времени с помощью интеграла Дюамеля. Составив программу для ЭВМ, или воспользовавшись программой "Определение реакции цепи на импульс заданной формы с помощью интеграла Дюамеля (DML) вычислить значения напряжения на выходе: для 10-15 моментов времени и построить графики U2(t)
3.1. Переходная характеристика цепи.
Вычислим переходную характеристику цепи, как реакцию на входное воздействие в виде единичной функции 1(t).
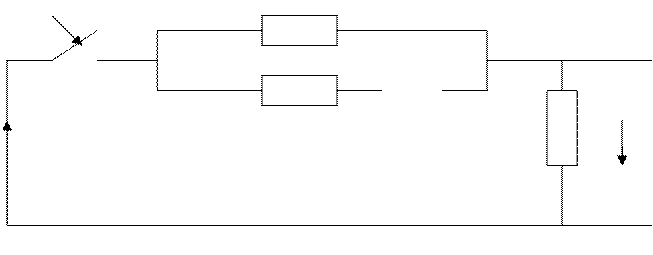R
 |
I(0+) R L R U2(t)
1. t(0-), U2(0-) =0 B.
2. t(0+), U2(0+)
= 
B.
3. t( ∞), U2(ПР) =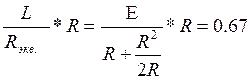
В
R
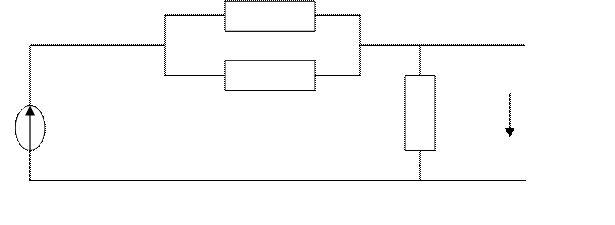
E R R U2(ПР)
Общая формула для нахождения переходной характеристики цепи
gu(t) = U2(ПР) + (U2(0+) – U2(ПР))*e-t/τ=0.67-0.17e-t/τ
Для нахождения τ запишем:
τ=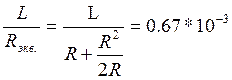
;
Получим переходную характеристику
gu(t)= U2(ПР) + (U2(0+) – U2(ПР))*e-t/τ =0.67-0.17*e-1492.5t
3.2 Анализ входного сигнала
Рассмотрим входной сигнал ( Рис. 2):
Весь отрезок времени O≤ t <∞ разбивается на три интервала. Границы интервалов приходятся на моменты времени t0=0 мс, t1=2 мс, t2= 4 мс.
В пределах интервала t1≤ t < t2 входной сигнал описывается уравнением:
U1(t1≤ t < t2)=15-2500*t В.
1) Найдем скачки напряжений на входном сигнале в моменты времени t0=0 мс, t1=2 мс, t2= 4 мс:
U1(0)=5 В;
U1(t1)= 5В;
U1(t2)=-5 В.
2) Найдем производные поведения сигнала на участках
U1’(t0), U1’(t1) и U1’(t2) :
U1’(t0)=0 B/c;
U1’(t1)=-2500 B/c;
U1’(t2)=0 B/c/
3.3. Запишем интеграл Дюамеля для каждого интервала цепи:
Интервал 0 ≤ t < t1.
U2(t)= U1(0)gu(t)+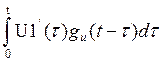
=5*(0.67-0.17* e-1492,5t )+0=
=3.35-0.85*e-1492,5t ;
Интервал t1 ≤ t < t2.
U2(t)= U1(0)gu(t)+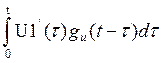 
+
U1(t1)gu(t-t1)+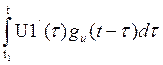
=
=3.35-0.85* e-1492,5t+5*(0.67-0.17* e-1492,5(t-2*10
)+
+
e-1492,5(t-τ)
) dτ= 10.05-17.92* e-1492,5t -1675*t+0.285-5.724* e-1492,5t =10.335-1675*t-23.644*e-1492,5t
;
Интервал t ≥ t2.
U2(t)= U1(0)gu(t)+ +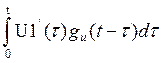
U1(t1)gu(t-t1)+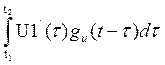 
+
U1(t2)gu(t-t2 ) =3.35-0.85* e-1492,5t+5*
*(0.67-0.17 e-1492,5(t-2*10))+
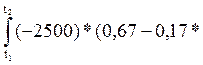*e-1492,5(t-τ)
) dτ-
-5*(0.67-0.17*e-1492,5(t-4*10))=483.168*
e-1492,5t.
3.4. Напряжение на выходе.
Подставляя полученные данные в программу DML, получаем следующие значения U2(t)- Таблица 1.
Таблица 1 –Значения U2(t), вычисленные с помощью интеграла Дюамеля.
|
t, мс |
0 |
0,33 |
0,67 |
1 |
1,33 |
1,67 |
t1- |
t1+ |
2.33 |
2.67 |
3 |
3.33 |
3.67 |
t2- |
t2+ |
|
U2, В |
2,5 |
2,83 |
3,03 |
3,16 |
3,23 |
3,28 |
3,31 |
5,81 |
5,71 |
5,44 |
5,06 |
4,61 |
4,13 |
3,62 |
1,18 |
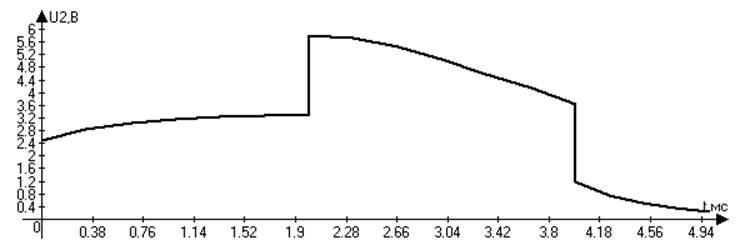
Рис. 3 График зависимости выходного сигнала от времени
4.Вычисление спектра сигнала на выходе цепи U2(jω).
4.1 Спектральная плотность входного сигнала.
Для нахождения спектральной плотности входного сигнала функция входной сигнал U1(t) представляется в виде суммы шести простейших функций:
;
;
;
;
.
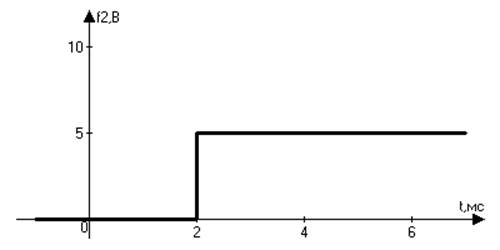
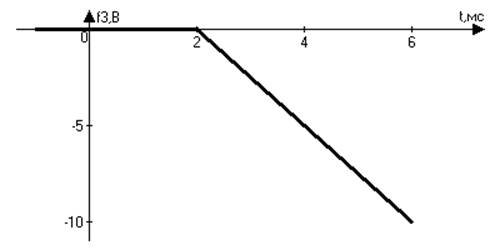
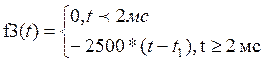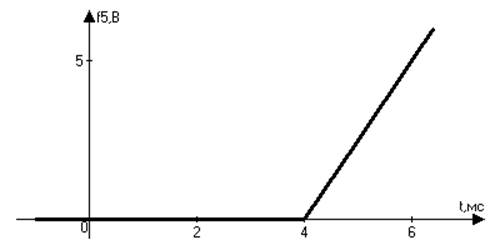
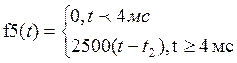Находим изображение входного сигнала:
F1(P)=
;
F2(P)= 
*e-0.002p ;
F3(P)= 
*e-0.002p ;
F4(P)= 
*e-0.004p ;
F5(P)= 
*e-0.004p ;
Изображение входного сигнала записывается как сумма изображений “простейших” функций:
F(P)= F1(P)+ F2(P)+ F3(P)+ F4(P) + F5(P);
F(P)= 
+*e-0.002p *e-0.002p+ *e-0.004p -
*e-0.004p .
Заменяя р→jω получаем спектральную плотность входного сигнала:
U1(jω)= 
+*e-0.002 jω 
*e-0.002jω+ 
*
e-0.004jω -*e-0.004jω = =*(1+
e-0.002jω - e-0.004jω)- *(
e-0.002jω - e-0.004jω)=
=
=
+
+j
.
Теперь получим формулу для амплитудной характеристики спектральной плотности входного сигнала
U1(ω)=
;
Формула для фазовой характеристики сигнала
Φ1(ω)=arctg 
.
Вычислив значения плотности входного сигнала, получили следующую таблицу (с помощью программы «Frean»):
Таблица 2- Спектр входного сигнала
|
F,кГц |
U1,мВ |
Φ1,градус |
|
0 |
25 |
0 |
|
0.2 |
8.145 |
165.89 |
|
0.4 |
4.238 |
73.879 |
|
0.6 |
2.885 |
95.484 |
|
0.8 |
1.44 |
348.71 |
|
1 |
0.797 |
90.365 |
|
1.2 |
1.077 |
179.86 |
|
1.4 |
1.22 |
78.041 |
|
1.8 |
0.658 |
351.73 |
|
2 |
0.398 |
90.729 |
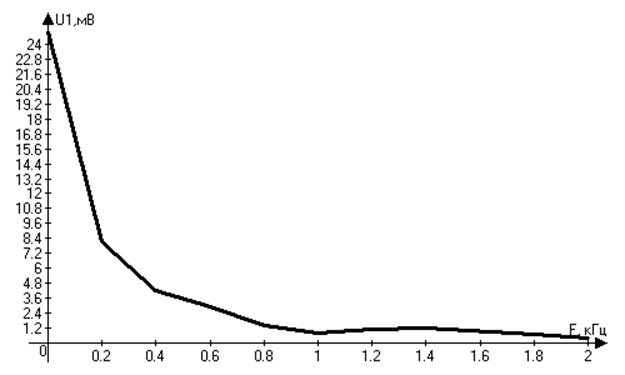
Рисунок 4. График амплитудной характеристики входного сигнала.
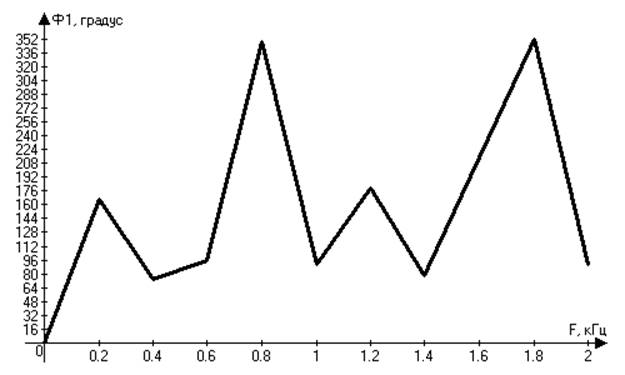
Рисунок 5. График фазовой характеристики входного сигнала.
4.2 AЧXи ФЧХ передаточной функции цепи.
Передаточная функция
по напряжению цепи, изображенной на рис. 1
H(jω)=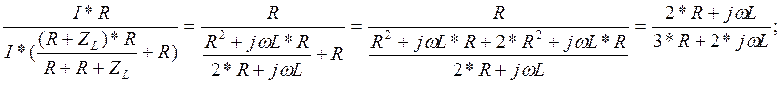
Амплитудно-частотная характеристика (АЧХ) этой цепи:
H(ω)=
Фазо-частотная характеристика ФЧХ ее:
(ω)=
–
=
– 
;
С помощью программы FREAN рассчитаем значения H(ω) и Ф(ω) и построим их графики:
Таблица 3-АЧХ и ФЧХ .
|
F,кГц |
H |
φ |
|
0 |
0.667 |
0 |
|
0.2 |
0.604 |
-7.816 |
|
0.4 |
0.549 |
-7.687 |
|
0.6 |
0.526 |
-6.255 |
|
0.8 |
0.516 |
-5.086 |
|
1 |
0.51 |
-4.234 |
|
1.2 |
0.507 |
-3.608 |
|
1.4 |
0.505 |
-3.135 |
|
1.8 |
0.503 |
-2.476 |
|
2 |
0.503 |
-2.238 |
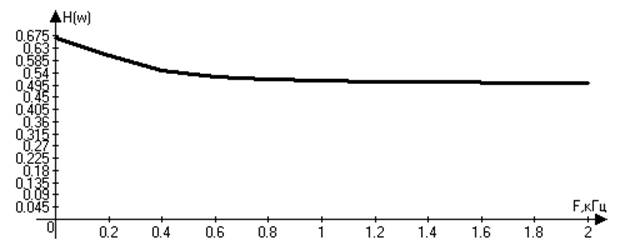
Рисунок 6. График АЧХ .
Рисунок 7. График ФЧХ .
4.3 Спектральная плотность выходного сигнала.
Амплитудная характеристика спектральной плотности сигнала на выходецепи записывается в виде:
U2(
)=U1()*H()= =
*
*
Фазо-частотная характеристика имеет вид:
=
+
+– .
Вычислив значения плотности выходного сигнала, получили следующую таблицу (с помощью программы «Frean»):
Таблица 4-Спектр выходного сигнала.
|
F,кГц |
U2,мВ |
Φ2,градус |
|
0 |
16.667 |
0 |
|
0.2 |
4.916 |
158.08 |
|
0.4 |
2.325 |
66.192 |
|
0.6 |
1.517 |
89.229 |
|
0.8 |
0.743 |
343.63 |
|
1 |
0.407 |
86.131 |
|
1.2 |
0.546 |
176.26 |
|
1.4 |
0.617 |
74.906 |
|
1.8 |
0.331 |
349.25 |
|
2 |
0.2 |
88.491 |
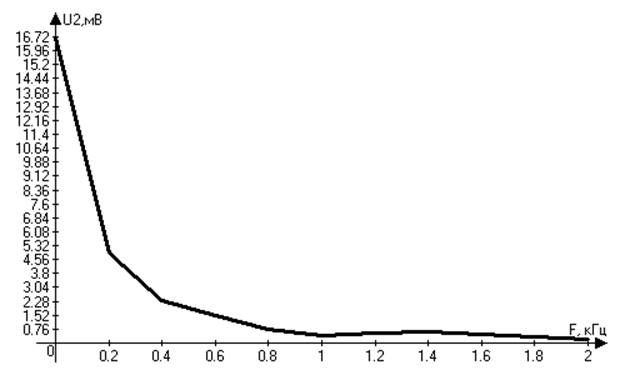
Рисунок 8. График амплитудной характеристики выходного сигнала.
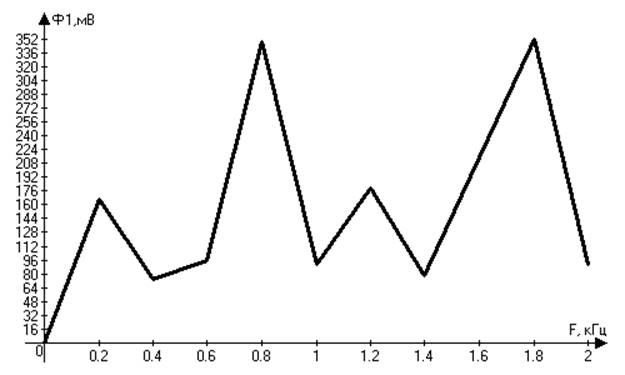
Рисунок 9. График фазовой характеристики выходного сигнала
4.4 Импульсная характеристика цепи
Временные и частотные характеристики цепи связаны между собой формулами преобразования Фурье. По найденной в п.3.1, переходной характеристике вычисляется импульсная характеристика цепи:
gu(t)=0.67-0.17*e-1492.5;
Общая формула для нахождения импульсной характеристики цепи:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
