Аппроксимация зашумленных сигналов полиномиальными функциями по методу наименьших квадратов (одномерная полиномиальная регрессия)

Спецглавы информатики

Методические указания к курсовой работе

Тема 1

Аппроксимация зашумленных сигналов полиномиальными функциями по методу наименьших квадратов

(одномерная полиномиальная регрессия)

Исходные данные.

Задана таблица отсчетов зашумленного дискретизированного сигнала (дискретная функция  ).

k	0	1	2				n

n – количество отсчетов сигнала (значений X _i и Y_i  ).

Цель работы: Создать приложение для аппроксимации зашумленных сигналов полиномиальными функциями по методу наименьших квадратов (реализации одномерная полиномиальная регрессия). При этом аппроксимирующая функция определяется в виде полиномиальной функции

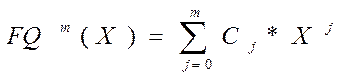,                 (1), где  m – степень полинома FQ(X),

 - коэффициенты искомого полинома, которая будет наиболее близкой к исходной функции  заданной табличными значениями, т.е. необходимо определить вектор коэффициентов полинома , при котором полиномиальная функция FQ(X) будет наиболее близкой к заданным в таблице точкам.

В качестве критерия близости используем квадратичный функционал

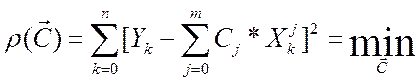,     (2)

где    - искомый вектор коэффициентов полинома.

Методика решения задачи.

Для реализации метода наименьших квадратов в качестве критерия близости используем квадратичный функционал (2).

Квадратичный функционал (2) имеет один экстремум (минимум). Минимум рассматриваемого квадратичного функционала находится из условия равенства нуль всех частных производных функционала 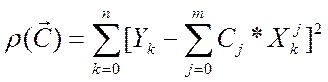, т.е. 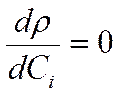при .      (3)

Частные производные определяются как:

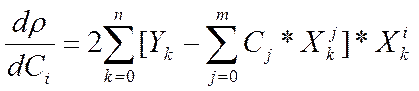.   .                   (4)

Приравняв нулю частные производные

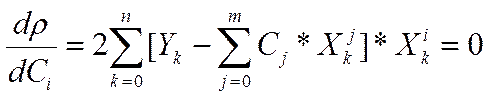,     ,        (5)

получаем систему линейных уравнений в виде

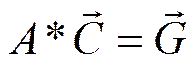,                                       (6)

где   матрица коэффициентов уравнения (матрица Грамма),

 - вектор правых частей системы уравнений.

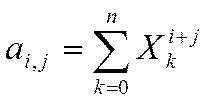
        (7)

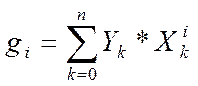
Искомые коэффициенты аппроксимирующего полинома (вектор ) получаем путем решения системы линейных уравнений (6). В матричном виде вектор  определяется  как:

                         (8)

Для поиска параметров аппроксимирующего полинома можно использовать функции Excel. В Excel есть матричные функции:

МОБР – обратная матрица

МУМНОЖ – умножение матриц.

Для решения системы уравнений в Excel в ячейки листа вводятся элементы матрицы А и вектора G. Затем мышкой выделяется диапазон ячеек, где располагается вектор параметров аппроксимации, и вводится формула        =МУМНОЖ(МОБР(Диапазон А);Диапазон G).

Затем нажимается комбинация клавиш [<Ctrl>+<Shift>+<Enter>].

В диапазоне ячеек, куда была введена формула, появятся искомые значения параметров аппроксимации.

Качество аппроксимации будем оценивать квадратичным критерием близости. При этом будем оценивать среднеквадратичным значением  σ_ρ  отклонения значений полинома в заданных точках X_i от заданных в таблице значений  Y_i .

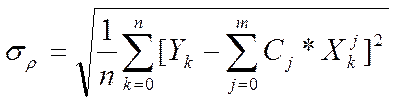.    (9)

Порядок выполнения курсовой работы

Исходными данными для выполнения курсовой работы являются:

Mm – максимальная степень аппроксимирующего полинома,

n  - количество отсчетов зашумленного сигнала,

Таблица отсчетов зашумленного дискретизированного сигнала.

i	0	1	2				n

При выполнении работы необходимо по  заданным значениям (X_i , Y_i ) определить коэффициенты аппроксимирующего полинома  для степеней аппроксимирующего полинома  m = 1, 2,     Mm.  Полученные наборы коэффициентов аппроксимирующего полинома  при m = 1, 2,     Mm записать в таблицу коэффициентов.

m	C0	C1	C2		CMm
1	C0,1	C1,1
2	C0,2	C1,2	C2,2
Mm	C0,Mm	C1.Mm	C2,Mm		CMm,Mm

Для каждого значения m = 1, 2,     Mm построить графики (Mm графиков) аппроксимирующих полиномов 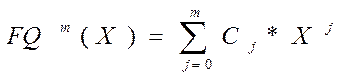при X изменяющемся от  до  с задаваемым шагом dX. На графиках изобразить также заданные точки (X _i , Y_i ).

Для каждого значения m = 1, 2,     Mm вычислить погрешности аппроксимации

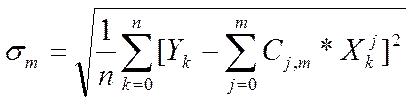
Полученные значения занести в таблицу.

m	1	2		Mm
σ	σ1	σ2		σMm

Результатом курсовой работы является получение зависимости параметров аппроксимации (коэффициентов аппроксимирующего полинома и погрешности аппроксимации) от степени аппроксимирующего полинома для заданного набора отсчетов (X _i , Y_i ) и определенияминимальной степени полинома Mmin, после которой параметры аппроксимации практически не изменяются ,т.е. при m>Mmin параметры аппроксимируюшего полинома (вид функции регрессии) практически не изменяются.

Курсовая работа должна быть реализована в виде приложения на Visual Basic (либо на другом языке программирования). Курсовая работа может быть также выполнена в системе Mathcad (Matlab).

По курсовой представляется отчет на бумаге с титульным листом и описанием выполнения работы. В отчете должны быть приведены описания численных методов , объектов графического интерфейса и исходные тексты процедур программного приложения. К отчету прилагается программное приложение на CD – диске