Методические указания по выполнению курсовой работы по дисциплине «Электропривод переменного тока»

перевода в абсолютные единицы необходимо определить номинальный ток и базовое сопротивление:

, А	(1)
, Ом.	(2)

С учетом формулы (2.2) параметры Г-образной упрощенной схемы замещения в абсолютных единицах определятся:

, Ом;	(3)
, Ом;	(4)
, Ом;	(5)
, Ом;	(6)
, Ом.	(7)

Г-образная упрощенная схема замещения в абсолютных единицах изображена на рис. 1.

Рисунок 1 - Г-образная упрощенная схема замещения в абсолютных единицах

На рис. 1 в цепи намагничивания показан комплекс полного сопротивления статора .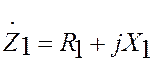

По номинальным данным определяются число полюсов  и синхронная частота вращения :

,	(8)
, .	(9)

Расчеты по формулам (1) – (9) выполнить в среде MathCad.

4. Расчет мощности, потребляемой из сети

Активная, реактивная и полная мощности, потребляемые из сети в номинальном режиме работы, определяются по формулам:

Вт;	(10)
, Вар;	(11)
, ВА.	(12)

Расчеты по формулам (10) – (12) выполнить в среде MathCad.

5. Расчет характерных точек механической характеристики

Механическая характеристика асинхронного двигателя (рис. 2) имеет характерные точки:

точка идеального холостого хода , точка номинального режима , точка критического момента , точка минимального момента , точка короткого замыкания .

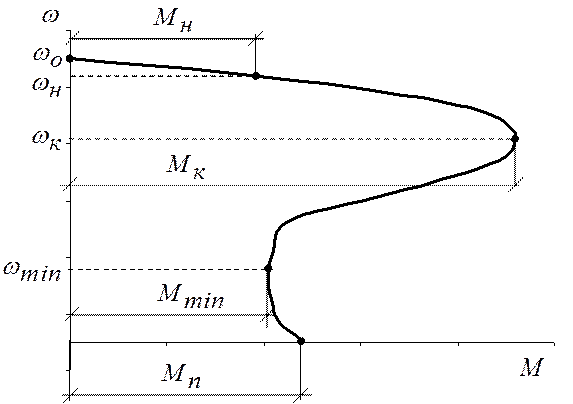
Рисунок 2 - Механическая характеристика асинхронного двигателя

5.1. Точка идеального холостого хода,

Частота вращения при идеальном холостом ходе рассчитывается по формуле (9):

, .

(13)

5.2. Точка номинального режима .

Номинальный момент:

, Нм.

(14)

Номинальное скольжение, рассчитанное по параметрам схемы замещения, можно найти из выражения:

,

(15)

где .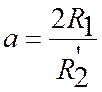

Положив в выражении (15) , получим:

,

(16)

Разрешим уравнение (16) относительно :

.

.

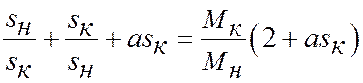(17)

Приведем уравнение (17) к каноническому виду квадратного уравнения:

.

(18)

Решение квадратного уравнения (18) имеет вид:

.

(19)

Знак  относится к генераторному режиму, знак  к двигательному режиму работы.

Номинальная расчетная частота вращения:

, .

(20)

5.3. Точка критического момента :

, Нм;	(21)
;	(22)
,	(23)

5.4. Точка минимального момента  по данным схемы замещения не рассчитывается. Минимальный момент обусловлен влиянием высших гармоник и вытеснением тока в обмотке ротора. Данные факторы не учитываются Г-образной схемой замещения.

5.5. Точка короткого замыкания .

Момент при коротком замыкании  определяется по формуле (15), если в ней положить :

, Нм.

(24)

Расчеты по формулам (13), (14), (19) – (24) выполнить в среде MathCad.

6. Построение механической и энергомеханической характеристик при номинальных напряжении и частоте

Уравнение механической характеристики представляет собой зависимость скольжения  (частоты вращения ) от момента :

, Нм.

(25)

Энергомеханические характеристики представляю собой зависимость токов  статора и ротора  от скольжения .

Ток  вычисляется по формуле:

, А.

(26)

Ток  является векторной суммой токов ротора  и тока намагничивания . Модуль тока статора в этом случае будет равен:

, А.

(27)

где 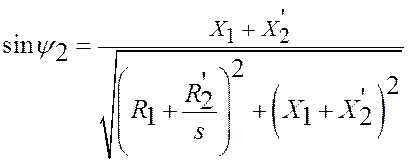 - сдвиг по фазе тока ротора.

Механическую и энергомеханические характеристики в соответствии с уравнениями (25) – (27) для двигательного режима работы построить на одном графике в среде MathCad.

7. Выбор закона регулирования  в зависимости от заданной характеристики момента нагрузки

В задании на курсовую работу (приложение 1) указана характеристика момента нагрузки:

·  постоянный момент нагрузки,

·  нелинейно спадающий момент нагрузки,

·  вентиляторный характер момента нагрузки.

В соответствии с вариантом задания момент нагрузки рассчитывается по одной из следующих формул.

Постоянный момент нагрузки. В этом случае принимается, что момент нагрузки равен номинальному моменту двигателя:

.

(28)

Нелинейно спадающий момент нагрузки:

,

(29)

где  - частота вращения ротора, ;  - коэффициент, определяющий крутизну изменения момента нагрузки, .

Момент вентиляторной нагрузки:

,

(30)

где  - момент холостого хода, Нм; 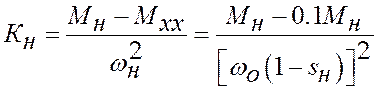 - коэффициент, определяющий крутизну изменения момента нагрузки, .

8. Построение механических характеристик при выбранном законе регулирования

При изменении частоты напряжения на статоре будут изменяться синхронная частота вращения , скольжение  и индуктивные сопротивления рассеивания статора и ротора :

,	(31)
,	(32)
.	(33)

С учетом выражений (31), (33) уравнение (25) механической характеристики