


















означає, що для досягнення тієї ж
точності можна брати менше число n ділянок розбиття, а при тому ж кроці h вона
дає меншу абсолютну і відносну похибки.
2. Постановка задачі
Завдання курсової роботи на тему „Використання підпрограм та функцій користувача при роботі з масивами” належить до обчислювального класу задач.
Метою розв’язання даної роботи є поетапне вирішення таких завдань:
1.
Обчислити елементи
квадратної матриці ![]() (і=1,
2,...5; j = 1,2,...5).
(і=1,
2,...5; j = 1,2,...5).
2.
Використовуючи елементи
матриці ![]() обчислити елементи вектора
обчислити елементи вектора ![]() (і =1, 2,...5), як суму елементів головної діагоналі
та п’ятого стовпця матриці.
(і =1, 2,...5), як суму елементів головної діагоналі
та п’ятого стовпця матриці.
3. Обчислити значення функції за формулою ![]() на
основі знайдених елементів вектора
на
основі знайдених елементів вектора ![]() з використанням
вкладених циклів.
з використанням
вкладених циклів.
4. Завдання. обчислити інтеграл ![]() , використовуючи формулу Сімпсона при n=100. Коефіцієнти
виразу
, використовуючи формулу Сімпсона при n=100. Коефіцієнти
виразу ![]() скопіювати
з відповідних елементів вектора Х, який було створено вище.
скопіювати
з відповідних елементів вектора Х, який було створено вище.
3. Алгоритм розв’язання задачі
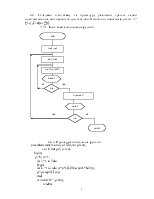
3.1. Розглянемо першу задачу. Побудуємо блок-схему та запишемо процедуру реалізації даної задачі. Слід відмітити, що задача реалізується за допомогою вкладених циклів. Змінна циклу і є змінною зовнішнього циклу, а змінна циклу j – внутрішнього циклу.
3.1.1. Блок-схема для створення матриці ![]() , елементи якої визначаються за формулою
, елементи якої визначаються за формулою ![]()
3.1.2. Процедура реалізації
підпрограми знаходження матриці ![]() , елементи якої визначаються за формулою
, елементи якої визначаються за формулою ![]()
procedure mas (var a: arr);
var i,j: integer;
begin
for i:=1 to 5 do
begin
for j:=1 to 5 do
begin
a[i,j]:=(3+i)/(i+j)*sqrt(exp(3*ln(i))+sqr(j))+exp((i-j)*ln(2));
write('a[',i,',',j,']=',a[i,j]:6:4,' ' );
end;
writeln
end;
end;
Дана
процедура формує матрицю ![]() та виводить на
екран елементи матриці по стрічках. Тіло процедури реалізовано за допомогою
операторів циклу з параметром, оскільки крок змінних циклу дорівнює 1.
та виводить на
екран елементи матриці по стрічках. Тіло процедури реалізовано за допомогою
операторів циклу з параметром, оскільки крок змінних циклу дорівнює 1.
3.2. Складемо блок-схему та процедуру реалізації
другої задачі, посилаючись на дані першої задачі. Використовуючи елементи
матриці ![]() обчислити елементи вектора
обчислити елементи вектора ![]() (і =1, 2,...5), як суму елементів головної діагоналі
та п’ятого стовпця матриці.
(і =1, 2,...5), як суму елементів головної діагоналі
та п’ятого стовпця матриці.
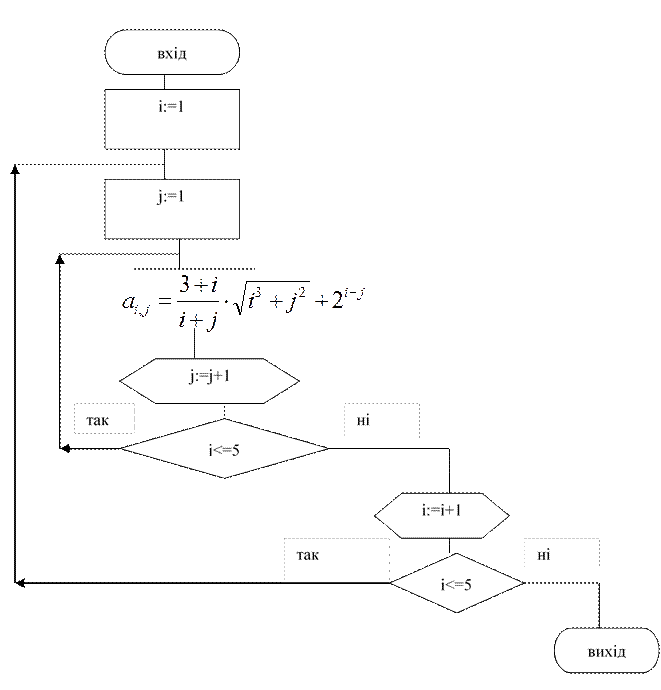
3.2.1. Блок-схема формування вектора ![]()
3.2.2. Процедура реалізації підпрограми формування вектора ![]()
Procedure vector (a: arr; var x: array of real);
var i,j: integer;
begin
for i:=1 to 5 do
begin
x[i]:=a[i,i]+a[i,5];
write ('x[',i,']= ',x[i]:3:3,' ');
end;
end;
Дана процедура формує вектор та виводить на екран вектор у вигляді стрічки.
3.3. Складемо блок-схему та процедуру реалізації
третьої задачі посилаючись на дані першої та другої задачі. Обчислити значення
функції ![]()
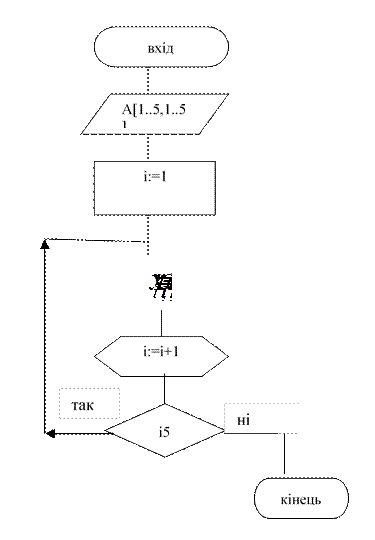
3.3.1. Блок-схема обчислення функції
3.3.2. Процедура обчислення функції
procedure func(x:array of real;var g:real);
var k: integer; p: real;
begin
g:=0; p:=1;
for i:=1 to 5 do
begin
for k:=1 to i do p:=p*x[k]/(k+exp(k*ln(2)));
g:=g+sqr(x[i])+p;
end;
writeln('G= ',g:6:4);
readln
end;
3.5. Запишемо програму розв’язку задач першої частини, опираючись на раніше створені процедури
PROGRAM kurs6;
uses crt;
type arr=array [1..5,1..5] of real;
type xrr=array [1..5] of real;
var a: arr;
x: xrr;
si, g: real; i,j: integer;
procedure mas (var a: arr);
var i,j: integer;
begin
for i:=1 to 5 do
begin
for j:=1 to 5 do
begin a[i,j]:= (3+i)/(i+j)*sqrt(exp(3*ln(i))+sqr(j))+exp((i-j)*ln(2));
write('a[',i,',',j,']=',a[i,j]:6:4,' ' );
end;
writeln
end; end;
Procedure vector (a: arr; var x: xrr);
var i,j: integer;
begin
for i:=1 to 5 do
begin
x[i]:=a[i,i]+a[i,5];
write ('x[',i,']= ',x[i]:3:3,' ');
end; end;
procedure func(x: xrr;var g:real);
var k: integer; p: real;
begin
g:=0;p:=1;
for i:=1 to 5 do
begin
for k:=1 to i do p:=p*x[k]/(k+exp(k*ln(2)));
g:=g+sqr(x[i])+p;
end;
writeln('G= ',g:6:4);
end;
procedure simpson( x: xrr; var si: real);
var i,k:integer; h,z,a,b,f,f1:real;
begin
writeln('a,b'); readln(a,b);
h:=(b-a)/100; z:=b;
f1:=(x[1]+x[2]*z+x[3]*z*z +x[4]*z*z*z+x[5]*exp(4*ln(z)))/(exp(z)+1.5);
k:=1; z:=a;
f:=(x[1]+x[2]*z+x[3]*z*z +x[4]*z*z*z+x[5]*exp(4*ln(z)))/(exp(z)+1.5);
si:=f+f1;
for i:=1 to 99 do
begin
z:=z+h;
f:=(x[1]+x[2]*z+x[3]*z*z +x[4]*z*z*z+x[5]*exp(4*ln(z)))/(exp(z)+1.5);
si:=si+(3+k)*f;
k:=-k;
end;
si:=si*h/3;
writeln('integral=',si);
readln
end.
4. Результати виконання програми
1. Елементи матриці роздруковуємо у вигляді таблиці:
a[1,1]=3.8284 a[1,2]=3.4814 a[1,3]=3.4123 a[1,4]=3.4235 a[1,5]=3.4618
a[2,1]=7.0000 a[2,2]=5.3301 a[2,3]=4.6231 a[2,4]=4.3325 a[2,5]=4.2283
a[3,1]=11.9373 a[3,2]=8.6813 a[3,3]=7.0000 a[3,4]=6.1207 a[3,5]=5.6583
a[4,1]=19.2872 a[4,2]=13.6206 a[4,3]=10.5440 a[4,4]=8.8262 a[4,5]=7.8375
a[5,1]=30.9666 a[5,2]=20.9804 a[5,3]=15.5758 a[5,4]=12.5550 a[5,5]=10.7980
2. Результати реалізації пункту 2 поставленої задачі
x[1]= 7.290 x[2]= 9.558 x[3]= 12.658 x[4]= 16.664 x[5]= 21.596
3. Значення обчисленої функції
G= 1595.1367
Висновки
В даній курсовій роботі розроблено алгоритми обчислювального характеру у відповідності з завданням до варіанту № 6 Написані програми та отримані результати наведено вище під час опису виконання роботи. виконання роботи складалось із кількох етапів. Спершу було здійснено постановку задачі та опрацьовано відповідний матеріал із літератури. На наступному етапі розроблено алгоритми вирішення поставлених задач. Це питання розв’язувалось паралельно із їх програмним вирішенням. На останньому етапі під час підготовки звіту було вивчено методи та вимоги оформлення звіту, засоби перенесення результатів із програми Паскаля в редактор Word, навики побудови ілюстрацій до блок-схем програм. Результати виконання програми вважаю правдивими з огляду на порівняння їх з перерахунком основних етапів розв’язку задачі.
Під час виконання даної курсової роботи я ознайомилась із використанням підпрограм та функцій користувача при роботі з масивами на прикладі написаних мною програм на мові Паскаль, набувши таким чином певних навиків програмування.
В результаті виконання курсової роботи значно розвинулись навички
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.