При
формировании схемы замещения источник питания Е
исключен путем закорачивания, так как это источник постоянного напряжения, ко
входу подключена ветвь источника сигнала, а к выходу – ветвь нагрузки. Для
обеспечения компактности функциональной математической модели и упрощения
процедуры ее формирования целесообразно использовать однородный координатный
базис. Анализ структурных особенностей схемы замещения показывает, что
контурный координатный базис обеспечит меньшую размерность матрично-векторных
параметров математической модели (система контурных уравнений будет иметь 4-ый
порядок, тогда порядок системы узловых уравнений будет равен 5). Кроме того,
схема замещения является планарной, что позволяет выбрать каноническую систему
независимых циклов, упростив структуру матрично-векторных параметров. Ветви
источника сигнала и нагрузки представлены внешними ветвями схемы замещения, что
упрощает выражения для схемных функций. Для использования контурного
координатного базиса все компоненты схемы замещения представлены как z-компоненты:
источник сигнала – источником ЭДС, нагрузка – сопротивлением ![]() ,
пассивные двухполюсники – соответствующими сопротивлениями. Разделительные
конденсаторы в схеме замещения учтены операторными сопротивлениями
,
пассивные двухполюсники – соответствующими сопротивлениями. Разделительные
конденсаторы в схеме замещения учтены операторными сопротивлениями 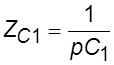 ,
,
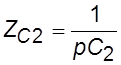 ,
базовый делитель представлен эквивалентным сопротивлением
,
базовый делитель представлен эквивалентным сопротивлением 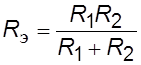 ,
элементы эмиттерной цепи – эквивалентным операторным сопротивлением
,
элементы эмиттерной цепи – эквивалентным операторным сопротивлением 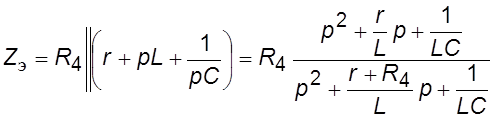 ,
где
,
где ![]() –
сопротивление, отражающие потери в последовательном колебательном контуре.
Сопротивление потерь главным образом обусловлено омическими потерями в катушке
индуктивности.
–
сопротивление, отражающие потери в последовательном колебательном контуре.
Сопротивление потерь главным образом обусловлено омическими потерями в катушке
индуктивности.
В качестве исходной модели биполярного транзистора будем использовать линейную малосигнальную высокочастотную Т-образную физическую эквивалентную схему, представленную на рис. 3.2.
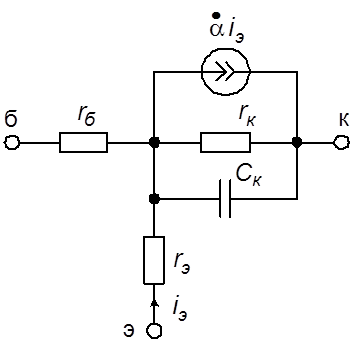
Рис. 3.2. Линейная малосигнальная высокочастотная Т-образная физическая эквивалентная схема биполярного транзистора
В
эквивалентной схеме ![]() –
омическое сопротивление области базы;
–
омическое сопротивление области базы; ![]() –
дифференциальное сопротивление обратно смещенного коллекторного перехода;
–
дифференциальное сопротивление обратно смещенного коллекторного перехода; ![]() –
дифференциальное сопротивление прямо смещенного эмиттерного перехода;
–
дифференциальное сопротивление прямо смещенного эмиттерного перехода; ![]() –
ёмкость коллекторного перехода;
–
ёмкость коллекторного перехода; 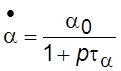 –
аппроксимация операторного изображения коэффициента передачи тока эмиттера;
–
аппроксимация операторного изображения коэффициента передачи тока эмиттера; ![]() –
статический коэффициент передачи тока эмиттера
–
статический коэффициент передачи тока эмиттера 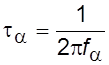 –
эквивалентная постоянная времени коэффициента передачи тока эмиттера;
–
эквивалентная постоянная времени коэффициента передачи тока эмиттера; ![]() –
предельная частота коэффициента передачи тока эмиттера.
–
предельная частота коэффициента передачи тока эмиттера.
Для формирования функциональной математической модели используем обобщенный матричный метод. Схема замещения усилителя с многополюсным компонентом и выбранной системой независимых циклов приведена на рис. 3.3.
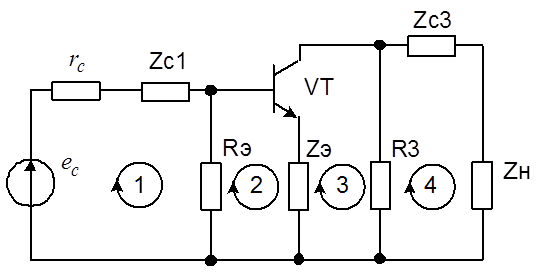
Рис. 3.3. Каноническая система независимых контуров
Укороченная матрица эквивалентных сопротивлений пассивной части схемы имеет вид:
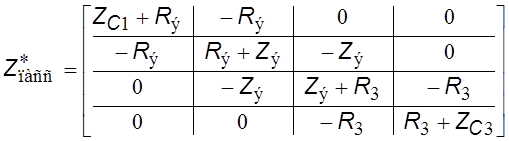 .
.
Неопределенная матрица сопротивлений биполярного транзистора, соответствующая эквивалентной схеме (рис. 3.2) имеет вид:
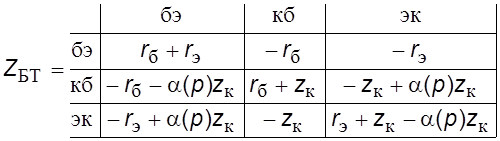 .
.
Матрица независимых циклов для сторон биполярного транзистора:
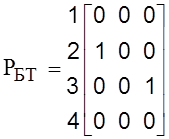 .
.
Укороченная матрица эквивалентных сопротивлений схемы формируется по выражению:
![]() .
.
4 Определение схемных функций
Рассматриваемый
избирательный усилитель по назначению относится к усилителям напряжения,
поэтому основными схемными функциями, характеризующими его качественные
технические показатели, являются коэффициент ![]() передачи
напряжения, входной импеданс
передачи
напряжения, входной импеданс ![]() и
выходной импеданс
и
выходной импеданс![]() .
.
Указанные схемные функции вычисляются на основе определителя и алгебраических дополнений укороченной матрицы эквивалентных сопротивлений. Поскольку ветви источника сигнала и нагрузки являются внешними ветвями схемы замещения, для схемных функций справедливы соотношения:
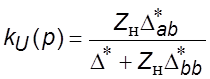 ,
,
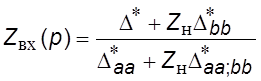 ,
,
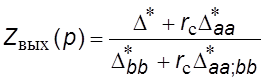 , где
, где
![]() –
простое несимметричное,
–
простое несимметричное, ![]() ,
,![]() –
простые симметричные,
–
простые симметричные, ![]() –
двухкратное простое симметричное алгебраические дополнения укороченной матрицы
эквивалентных сопротивлений схемы;
–
двухкратное простое симметричное алгебраические дополнения укороченной матрицы
эквивалентных сопротивлений схемы; ![]() –
определитель укороченной матрицы эквивалентных сопротивлений схемы;
–
определитель укороченной матрицы эквивалентных сопротивлений схемы; ![]() –
номер входного цикла;
–
номер входного цикла; ![]() –
номер выходного цикла.
–
номер выходного цикла.
Для
выбранной на схеме замещения (рис. 3.3) системы независимых циклов ![]() ,
,
![]() ,
поэтому выражения для схемных функций принимают вид:
,
поэтому выражения для схемных функций принимают вид:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.