Процесс применения моделей многономенклатурных поставок и влияние данного процесса на уровень запасов товарных позиций (располагаемых, наличных, средних)

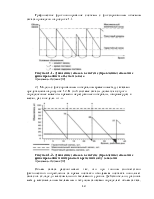
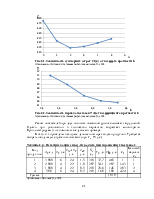
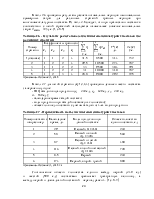
интервал времени между заказами рассчитывается для всех продуктов по формуле (3.3):

или же принимается фиксированным, как в нашем случае (.

При реализации модуля с различными вариантами спроса и исходными данными задачи, интервал времени между заказами варьировался около значения в 7 дней (.

3) За время выполнения заказа будет приниматься наибольшее значение  среди всех товарных позиций. В нашем случае это будет . Следовательно, поставка со всеми товарными позициями поставщика будет приходить спустя три дня после заказа.

В результате нескольких реализаций данной стратегии при различных генерациях спроса, мы получили следующие графики движения запаса (рис. 3.1 а, б, в):

а)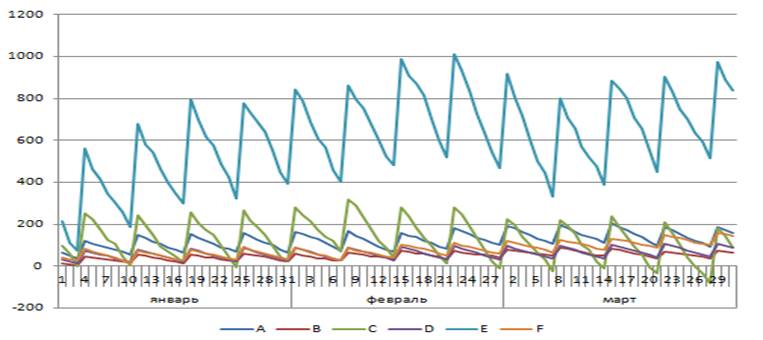

б)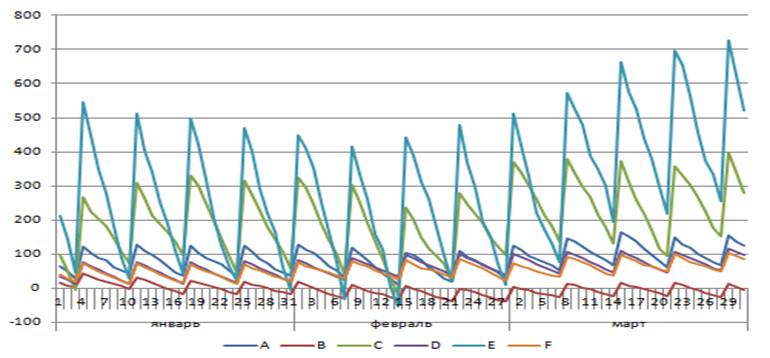

в)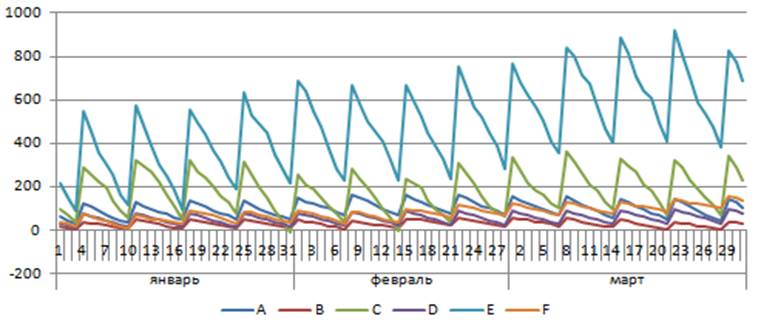

Рис 3.1 – Графики зависимых поставок при реализации стратегии (1-3) с учетом генерации различного спроса (а, б, в).

Примечание – Источник: собственная разработка.

Проанализировав графики на рис.3.1 (а, б, в), мы видим, что данная стратегия не всегда оптимальна, т.к. в случае реализаций а) и б) мы получаем:

- большое число дней дефицита по нескольким видам продукции;

- превышение величины максимального запаса ( ) по некоторым товарным позициям;

- профицит запасов некоторых продуктов в то время, как другие товарные позиции уходят в дефицит.

Для улучшения модели воспользуемся следующими решениями:

1) Рассчитаем величину  (интервал времени между заказами) на каждый день и за окончательный вариант возьмем среднее значение за 7 дней , которое будем использовать для расчета объема заказа каждой товарной позиции . Значение в 7 дней было выбрано на основании того, что, по условию задачи, заказ следует делать раз в 7 дней. Воспользуемся при расчетах формулами (3.4)-(3.5):

где     интервал времени между заказами для момента времени t, рассчитанный на основании среднего значения за 7 дней;

 интервал времени между заказами, рассчитанный для момента времени t с учетом спроса в момент времени t;      

спрос на товар n в момент времени t.

2) По тому же принципу, что и в п.1 (3.5), рассчитаем средние за 7 дней значения спроса с помощью формулы (3.6):

где      средний за 7 дней спрос, рассчит.для момента времени t по продукту n;

спрос на товар n в момент времени i.

3) Скорректируем размер поставки в соответствии с (3.4)-(3.6). Теперь будем рассчитывать объем поставок по формуле (3.7):

Такая методика расчета позволит нам точнее спрогнозировать необходимый объем поставок по каждому продукту с учетом прогнозируемого на неделю спроса на каждую товарную позицию.

4) Учтем величину располагаемого запаса во избежание ситуаций, когда заказывается излишнее количество товара, которого на складе достаточно (величина РЗ не достигла ТЗ по товарной позиции). Для этого будем отнимать от объема заказа товарной позиции n разницу между располагаемым запасом и точкой заказа по формуле (3.8):

Подставив формулу (3.7) в (3.8), получаем (3.9):

Проследим за реализациями модуля при различных генерациях спроса на товарные позиции поставщика по графикам на рис.3.2. (а,б,в):

а)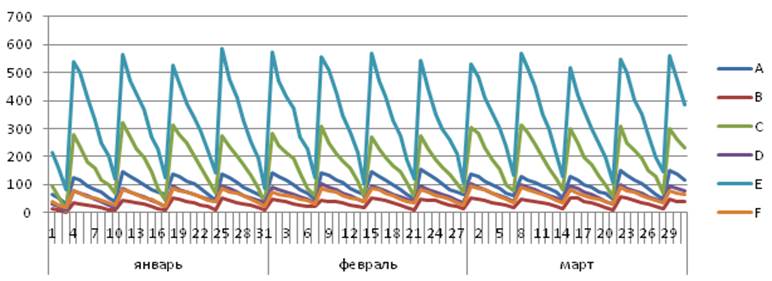

б)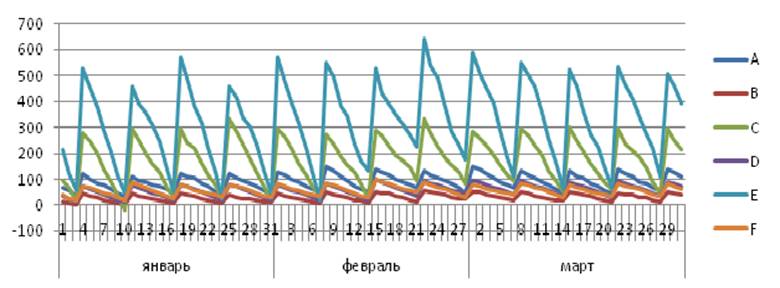

в)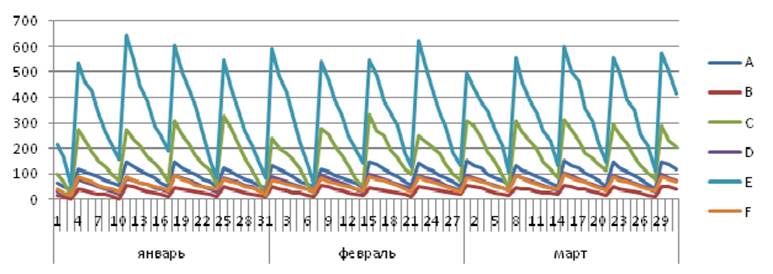

Рис.3.2 – Графики зависимых поставок при реализации модернизированной стратегии с учетом генерации различного спроса (а, б, в).

Примечание – Источник: собственная разработка.

Насколько заметно из графиков, запасы товаров не превышают максимальные значения, дефицит в 1 день возник только в одном случае вследствие повышенного спроса на товар и низких запасов на складе. Следовательно, данная модель более адекватно формирует график поставок и размер заказа каждой товарной позиции поставщика, чем исходная классическая модель с фиксированным интервалом времени между заказами.

Рассмотрим также несколько реализаций итоговой таблицы расчетных параметров (талблица 3.3):

Таблица 3.3 – Расчетные параметры многономенклатурной модели поставок в трех случаях генерации различного случайного спроса.

Примечание – Источник: собственная разработка.

Исходя из данных реализаций сделаем несколько выводов.

Разработанная модель является наилучшим решением для формирования многономенклатурных поставок, так как имеет ряд преимуществ:

1)  Запасы каждой позиции товара на складе не превышают пороговых значений максимального запаса (), то есть не создается ситуации переизбытка товара за складе, нехватки площадей склада под товарные позиции и т.д. В случае переизбытка товара на складе, компания вынуждена тратить дополнительные средства на содержание этого излишка, что не является экономичным;

2)  Количество дней дефицита в 90% реализации модуля (генерации случайного спроса) равно 0. В остальных случаях дефицит не превышает 1-2 дней, то есть