Глобальные балансовые модели, страница 3

Для практического построения такой матрицы в настоящее время нет достаточной информации. Модель Айзарда, так же, как и модель Дейли, имеет в основном теоретическое значение. Из рассмотрения этой модели вытекает общий методологический вывод, относящийся к построению экономико-математических моделей. Он заключается в необходимости перехода от регионального экономического планирования к региональному эколого-экономическому, учитывающему связи между производственными и экологическими процессами внутри эколого-экономической системы.

1.3.  МОДЕЛЬ В. ЛЕОНТЬЕВА.

Далее рассмотрим более подробно использование модели  Леонтьева – Форда для учета затрат на очистку промышленных стоков. В этом случае матрицы A₁₁, A₁₂, A₂₁, A₂₂, X₁, X₂, Y₁, Y₂  в уравнении (6.8) имеют следующий вид.

, где A₀ – матрица коэффициентов , характеризующих величину поставок i-го продукта для производства единицы j-го продукта без учета затрат на очистку стоков j-й отрасли.

, где  – матрица коэффициентов , отражающих затраты продукта i-й отрасли на очистку единицы объема стока j-й отрасли до санитарных норм.

, где A_v – диагональная матрица коэффициентов v_i, обозначающих объем сточных вод i-й отрасли, выпускаемый при производстве единицы продукции вида i и поступающих на очистные сооружения.

, поскольку предполагается, что процесс очистки не сопровождается появлением новых загрязнителей.

 – по-прежнему вектор валовых выпусков отраслей материального производства.

, где V – вектор с координатами V_i, определяющими весь объем сточных вод i-й отрасли.

 – вектор конечного продукта.

, поскольку основная цель моделирования состоит в учете затрат на очистку стоков, и загрязненные сточные воды, спускаемые в водоем без очистки, в модели не учитываются.

Получаем следующее матричное уравнение расширенного межотраслевого баланса:

.

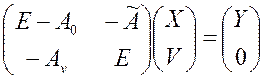Таким образом, от матрицы A традиционной схемы межотраслевого баланса мы перешли к матрице

.

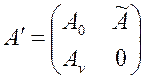В этом случае балансовое уравнение

преобразуется в систему уравнений

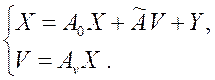                               (6.15)

Смысл уравнений первого вида состоит в том, что валовой выпуск i-й отрасли X_iдолжен покрывать спрос на ее продукт со стороны всех n отраслей материального производства, потребность в нем процессов очистки стоков всех отраслей и заданный конечный продукт Y_i. Уравнения второго типа определяют весь объем стоков i-й отрасли.

Подставив второе из уравнений (6.15) в первое, перепишем его в следующей форме:

.

Отсюда следует, что матрица технологических коэффициентов в случае учета затрат на очистку стоков имеет следующий вид:

.

Таким образом, выделение в межотраслевом балансе деятельности по очистке стоков ведет к изменению матрицы коэффициентов прямых затрат для всех отраслей, так как в исходной модели межотраслевые поставки продуктов для очистки стоков отрасли учитываются вместе с поставками продуктов, непосредственно идущих на производство. Поэтому коэффициенты прямых затрат a_ij, соответствующие отрасли материального производства, должны уменьшиться на величину средств, которые необходимы для обезвреживания стока, сопутствующего выпуску единицы продукции j-й отрасли:

.

Недостатки рассмотренной модели:

1.  Предположение о том, что затраты на очистные мероприятия прямо пропорциональны массе обрабатываемого загрязнителя, на практике выполняются не всегда. Например, при очистке сточных вод затраты на очистку пропорциональны не массе загрязнителя, а его концентрации.

2.  В сточных водах обычно присутствует несколько загрязнителей, и обезвреживание одного из них производится одновременно с обезвреживанием остальных. В этом случае выделить чистую отрасль, ликвидирующую один загрязнитель, затруднительно.

3.  Не учитываются затраты на утилизацию отходов, в которые превращается любое изделие, отслужившее свой срок.

Заключение

В условиях глобализации мировой экономики обеспечение жизнедеятельности мирового сообщества в планетарных масштабах становится главной задачей, носящей глобальный характер. Именно это обстоятельство обусловливает новый концептуальный подход — переход от понятия экономической системы к понятию эколого-экономической системы. Естественно, что в рамках такого подхода возникают новые специфические задачи и модели.

Список литературы

1.  Горстко А.Б., Угольницкий Г.А. Введение в моделирование эколого-экономических систем. Ростов н/Д.: Изд-во Ростов. ун-та, 1990.

2.  Гурман В.И., Батурин В.А. Математические модели управления природными ресурсами. Иркутск: Изд-во Иркут. ун-та, 1987.

3.  Леонтьев В., Форд Д. Межотраслевой анализ взаимодействия структуры экономики на окружающую среду // Экономика и мат. методы. 1972. Т. 8, вып. 3.