Гиперболические каустики, ограничивающие поле гауссова пучка вокруг оси симметрии (т. е. вокруг оси z) — однополостный гиперболоид вращения — называется каустической поверхностью или просто каустикой гауссова пучка. Это название пришло из геометрической оптики.
Отметим, что в продольном направлении гауссов пучок можно
разбить на три части. В центральной части, при![]() ,
поперечные размеры пучка сравнительно мало меняются с изменением z. В
двух же периферийных частях,z > b и z < — b, поперечные
размеры пучка заметно растут с ростом
,
поперечные размеры пучка сравнительно мало меняются с изменением z. В
двух же периферийных частях,z > b и z < — b, поперечные
размеры пучка заметно растут с ростом ![]() и
при больших
и
при больших![]() пропорциональны
пропорциональны
![]() .
.
Зависимость плотности энергии на оси пучка от
продольной координаты z определяется предэкспоненциальным множителем в (9).
Легко видеть, что эта плотность в центральной части пучка (![]() )
примерно постоянна, в периферийных же частях при
)
примерно постоянна, в периферийных же частях при![]() она
обратно пропорциональна
она
обратно пропорциональна![]() .
.
Рассмотрим теперь фазовое распределение в гауссовом пучке, т. е. найдем фазу в различных точках, занимаемых полем гауссова пучка. Фаза как функция г и z определяется частью показателя экспоненты в (6), заключенной в круглые скобки, перед которыми стоит мнимая единица г. Из этого выражения видно, что фаза квадратичным образом зависит от расстояния г до оси z и довольно сложным образом от z. Однако эти сведения не слишком наглядны. Более интересен другой подход, при котором отыскиваются условия постоянства фазы. Приравняв константе выражение в круглых скобках в (6), приходим к уравнению, связывающему z и r, т. е. определяющему некоторую поверхность в области, занимаемой пучком. Такая поверхность называется поверхностью постоянной фазы или волновым фронтом.
Представление о волновом фронте играет важную роль как в теории волн вообще, так и в теории лазерных резонаторов — в этом мы убедимся позднее.
Представим уравнение волнового фронта в виде
![]() (12)
(12)
где![]() —
то значение z, при котором
—
то значение z, при котором ![]() ,
т. е. координаты
,
т. е. координаты ![]() являются
координатами точки пересечения волнового фронта с осью z. Придавая
являются
координатами точки пересечения волнового фронта с осью z. Придавая ![]() те
или иные значения, будем получать различные волновые фронты данного гауссова
пучка. Правую часть в (12)
можно представить в виде
те
или иные значения, будем получать различные волновые фронты данного гауссова
пучка. Правую часть в (12)
можно представить в виде
![]()
Так как угол всегда меньше своего тангенса, то вычитаемое в этом выражении меньше, чем
![]()
Но это последнее выражение
значительно меньше, чем![]() ,
так как
,
так как ![]() (при
(при
![]() см,
см,
![]() см
см![]() ).
Следовательно, вторым слагаемым в (28) всегда можно пренебречь.
).
Следовательно, вторым слагаемым в (28) всегда можно пренебречь.
Теперь из уравнения (12) видно, что
разность![]() по
модулю всегда меньше
по
модулю всегда меньше![]() или
или![]() .
Действительно, так как множитель
.
Действительно, так как множитель
![]()
в левой части (12) всегда меньше или порядка ![]() ,
что следует, например, из уравнения гиперболы (11), то в целом из (12) следует,
что
,
что следует, например, из уравнения гиперболы (11), то в целом из (12) следует,
что ![]() .
Полагая, вследствие этого в левой части (12), получим для волнового фронта
уравнение параболы
.
Полагая, вследствие этого в левой части (12), получим для волнового фронта
уравнение параболы
![]() (13)
(13)
Таким образом, волновой фронт гауссова пучка имеет форму параболоида вращения. С хорошей точностью можно утверждать также, что этот фронт является сферическим, поскольку сфера радиуса
![]() (14)
(14)
и параболоид (13) практически совпадают при тех значениях r, где амплитуда пучка еще заметно отлична от нуля.
Следовательно, зависимость радиуса кривизны волнового фронта гауссова пучка от продольной координаты описывается соотношением (14) и показана на рис. 1.2, а. Кривизна волнового фронта — величина обратная радиусу кривизны — равна
![]()
и как функция показана на рис. 1.2, б.
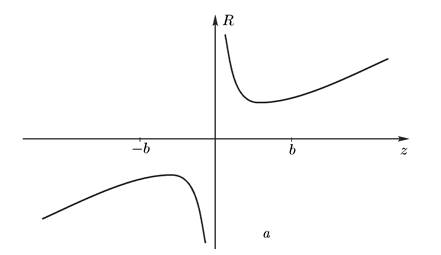
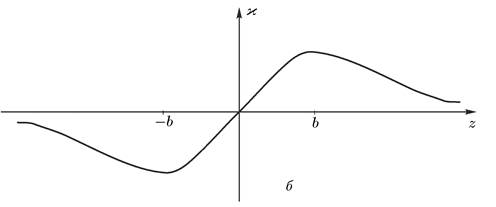
Рис. 1.2. Зависимость радиуса
кривизны R(а) и кривизны ![]() (б)
от продольной
(б)
от продольной
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.