Логика высказываний и элементы теории алгоритмов

Алгебра логики (алгебра высказываний)– раздел математической логики, в котором изучаются логические операции над высказываниями. Чаще всего предполагается, что высказывания могут быть только истинными или ложными, то есть используется так называемая бинарная или двоичная логика, в отличие от, например, троичной логики.

Базовыми элементами, которыми оперирует алгебра логики, являются высказывания.

Высказывание - это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным или ложным.

Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух), связанных логическими операциями.

Логические операции – операции, выполняемые в соответствии с правилами булевой алгебры. К ним относят операции: отрицания, логическое «и», логическое «или» и тождество (эквивалентность). На этих логических операциях основана работа вычислительных машин. С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).

Своим существованием наука «алгебра логики» обязана английскому математику Джорджу Булю, который исследовал логику высказываний.

Задание 1 Определите, истинно или ложно последнее высказывание, исходя из истинности или ложности предыдущих высказываний.

, , ;

Решение задачи

a	b	¬a	¬b	a˄¬b	a˅b	¬(¬a→b)˅a	(¬a→b)˅¬a	(a˄¬b)˅a)˄(a˅b)˅¬a
0	0	1	1	0	0	0	1	0
0	1	1	0	0	1	0	1	0
1	0	0	1	1	1	1	1	1
1	1	0	0	0	1	1	1	1

Ответ: исходя из условия эквивалентности, данное высказывание будет ложным.

2 Построение таблицы истинности

Таблица истинности – это такая таблица, в которой отражены все значения логической функции при всех возможных значениях, входящих в неё логически.

Алгоритм составления таблицы истинности:

1.  Подсчитать количество переменных n.

2.  Подсчитать количество строк m=2^n.

3.  Количество столбцов = n+ количество логических операций.
Основные логические функции

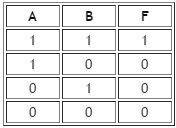
Рисунок 2.1 – Конъюнкция

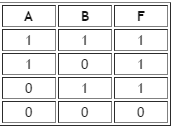
Рисунок 2.2- Дизъюнкция

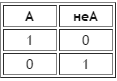
Рисунок 2.3 – Инверсия

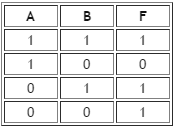
Рисунок 2.4 – Импликация

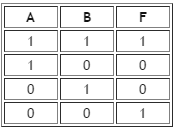
Рисунок 2.5 – Эквивалентность

Задание 2 Составьте таблицу истинности для формулы алгебры высказываний.

¬X ↔ ¬((Y ˅ ¬Z) → ¬(¬X ˅ ¬Y))

Решение задачи

11) ¬X↔((Y˅¬Z)→¬(X˅¬Y))

12) ¬(¬X)↔((Y˅¬Z)→¬(X˅¬Y))

X	Y	Z	¬X	¬Z	Y˅¬Z	¬Y	X˅¬Y	¬(X˅¬Y)	(Y˅¬Z)→¬(X˅¬Y)	11	12
0	0	0	1	1	1	1	1	0	0	0	1
0	0	1	1	0	0	1	1	0	1	1	0
0	1	0	1	1	1	0	0	1	1	1	0
0	1	1	1	0	1	0	0	1	1	1	0
1	0	0	0	1	1	1	1	0	0	1	0
1	0	1	0	0	0	1	1	0	1	0	1
1	1	0	0	1	1	0	1	0	0	1	0
1	1	1	0	0	1	0	1	0	0	1	0

3  ДИЗЪЮКТИВНАЯ НОРМАЛЬНАЯ ФОРМА

Дизъюктивная нормальная форма (ДНФ) - это нормальная форма, в которой булева формула имеет вид дизъюнкции конъюнкций литералов.

Любая булева формула может быть приведена к ДНФ. Для этого можно использовать закон двойного отрицания, закон де Моргана, закон дистрибутивности. Дизъюнктивная нормальная форма удобна для автоматического доказательства теорем.

Алгоритм приведения формулы к ДНФ:

1.  Выражение импликации через дизъюнкцию и отрицание, используя эквивалентность.

2.  Используя законы де Моргана, осуществить перенос всех отрицаний к переменным и сократить двойные отрицания, пользуясь законом двойного отрицания.

3.  Используя закон дистрибутивности, преобразовать выражение так, чтобы все конъюнкции выполнялись раньше дизъюнкций.

Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.

Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).

Задание 3 Приведите равносильными преобразованиями следующую формулу к ДНФ:  ¬(X ˄ Y) ˅ ¬(Z → Y)

Решение задачи

¬(X ˄ Y) ˅ ¬(Z → Y) = (¬X ˅ ¬Y) ˅ ¬(¬Z ˅ Y) = (¬X ˅ ¬Y) ˅ (Z ˄ ¬Y) =  = ¬X ˅ ¬Y ˅ Z ˄ ¬Y = ¬X ˅ ¬Y ˅ Z

4 КОНЪЮКТИВНАЯ НОРМАЛЬНАЯ ФОРМА

Конъюктивная нормальная форма (КНФ) – нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов.

Алгоритм приведения к КНФ аналогичен, только на шаге 3 делают так, чтобы все дизъюнкции встречались раньше конъюнкции.

Алгоритм приведения формулы к ДНФ:

1.  Выражение импликации через дизъюнкцию и отрицание, используя эквивалентность.

2.  Используя законы де Моргана, осуществить перенос всех отрицаний