Информатика и выч. техника \ Информатика

Вирішити СЛАР. Робота з матрицями. Нелінійне рівняння графічним та аналітичним методом

Страницы работы

20 страниц (Word-файл)

Скачать файл

Фрагмент текста работы

Знайти мінімум функції методом перебору та дихотомії(половинного поділу

5.2 Короткі теоретичні відомості

5.3 Програма

5.4 Результати

6.1 Знайти кубічну, квадратичну та лінійну апроксимацію заданих точок

6.2 Короткі теоретичні відомості

6.3 Програма

6.4 Результати

7.1 Знайти похідну функції в точці, використовуючи Matlab

7.2 Короткі теоретичні відомості

7.3 Програма

7.4 Результати

8.1 Знайти інтеграл функції, використовуючи Matlab

8.2 Короткі теоретичні відомості

8.3 Програма

8.4 Результати

1.1 Вирішити СЛАР

1.2 Короткі теоретичні відомості

Система лінійних алгебраїчних рівнянь(СЛАР) — в лінійній алгебрі це система лінійних рівнянь виду:

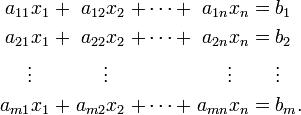
$\begin{alignat}{7} a_{11} x_1 &&\; + \;&& a_{12} x_2 &&\; + \cdots + \;&& a_{1n} x_n &&\; = \;&&& b_1 \\ a_{21} x_1 &&\; + \;&& a_{22} x_2 &&\; + \cdots + \;&& a_{2n} x_n &&\; = \;&&& b_2 \\ \vdots\;\;\; && && \vdots\;\;\; && && \vdots\;\;\; && &&& \vdots \\ a_{m1} x_1 &&\; + \;&& a_{m2} x_2 &&\; + \cdots + \;&& a_{mn} x_n &&\; = \;&&& b_m. \\ \end{alignat}$

Це система m лінійних рівнянь з n невідомими, де

$x_1,\ x_2,\ldots ,x_n$ - є невідомими,

$a_{11},\ a_{12},\ldots, a_{mn}$ - є коефіцієнтами системи,

$b_1,\ b_2,\ldots ,b_m$ - вільними членами.

Системи лінійних алгебраїчних рівнянь відіграють важливу роль у математиці, оскільки до них зводиться велика кількість задачлінійної алгебри, теорії диференціальних рівнянь, математичної фізики тощо, та областей фізики й техніки, де застосовуються ці математичні теорії.

1.3 Програма

clc

clear all

A=[[1.63,1.27,-0.84];[1.27,0.65,1.27];[-0.84,1.27,-1.21]]

B=[1.51;0.63;2.15]

x=inv(A)*B

1.4 Результат

A =

1.6300 1.2700 -0.8400

1.2700 0.6500 1.2700

-0.8400 1.2700 -1.2100

B =

1.5100

0.6300

2.1500

x =

-0.2564

1.5059

-0.0183

2.1 Робота з матрицями

2.2 Короткі теоретичні відомості

Матриця — математичний об'єкт, записаний у вигляді прямокутної таблиці чисел (чи елементів кільця) і допускаючий операції (додавання, віднімання, множення тамноження на скаляр). Зазвичай матриці представляються двовимірними (прямокутними) таблицями. Іноді розглядають багатовимірні матриці або матриці непрямокутної форми. В даній статті вони розглядатися не будуть..

Матриці є корисними для запису даних, що залежать від двох категорій, наприклад: для коефіцієнтів систем лінійних рівнянь та лінійних перетворень.

Горизонтальні лінії в матриці звуть рядками, вертикальні — стовпцями.

Матрицю, що складається з m рядків та n стовпців, називають матрицею m-на-n (або mn-матрицею), а m і n — її розмірністю.

Елемент матриці A, що знаходиться на перетині i-го рядка з j-им стовпчиком, називають i,j-им елементом або (i,j)-им елементом A.

Записують це як A_i,j чи A[i,j], або, в нотації мови програмування C, A[i][j].

Часто пишуть $\ A:=(a_{i,j})_{n \times m}$ для означення матриці A розмірності n x m, де кожен елемент матриці A[i,j] позначають як a_ij для всіх 1 ≤ i ≤ n та 1 ≤ j ≤ m.

Приклад

Матриця $\begin{bmatrix} 1 & 2 & 3 \\ 1 & 2 & 7 \\ 4 & 9 & 2 \\ 6 & 1 & 5 \end{bmatrix}$ є матрицею 4×3. Елемент A[2,3], або a_2,3 дорівнює 7.

2.3 Програма

clc

clear all

%Матриці

A=[[4,3,-2,-4];[3,-4,3,3];[-2,3,-2,5];[-4,3,5,-3]]

C=[[12,-2,1,-2];[-2,4,1,-2];[1,1,6,1];[-2,-2,1,4]]

%Обернені Матриці

V1=inv(A)

V2=inv(C)

%Транспоновані

B1=A'

B2=C'

%Детермінант Матриці

D1=det(A)

D2=det(C)

2.4 Результат

A =

4 3 -2 -4

3 -4 3 3

-2 3 -2 5

-4 3 5 -3

C =

12 -2 1 -2

-2 4 1 -2

1 1 6 1

-2 -2 1 4

V1 =

0.1566 0.1403 0.0371 -0.0067

0.1403 0.0356 0.1470 0.0935

0.0371 0.1470 0.0230 0.1359

-0.0067 0.0935 0.1359 -0.0045

V2 =

0.1613 0.2097 -0.0968 0.2097

0.2097 0.6559 -0.2258 0.4892

-0.0968 -0.2258 0.2581 -0.2258

0.2097 0.4892 -0.2258 0.6559

B1 =

4 3 -2 -4

3 -4 3 3

-2 3 -2 5

-4 3 5 -3

B2 =

12 -2 1 -2

-2 4 1 -2

1 1 6 1

-2 -2 1 4

D1 = 1347

D2 = 372.0000

3.1 Вирішити нелінійне рівняння графічним та аналітичним методом

3.2 Короткі теоретичні відомості

Алгебраїчним нелінійним рівнянням степеня n називається рівняння типу , де є многочленом степеня n.

Тобто, таке рівняння має такий вигляд:

$a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0 =\sum_{i=0}^{n}a_{i}x^{i} = 0$ , де називають коефіцієнтами рівняння. Також є переважно елементами множини дійсних, або комплексних чисел.

Найважливіші випадки нелінійних алгебраїчних рівнянь:

§ Квадратні рівняння ;

§ Кубічні рівняння ;

§ Біквадратні рівняння .

3.3 Програма

%e^(-x)-x=0

clc

clear all

%Графічний метод

ezplot('exp(-x)-x',[-8,8])

hold on

ezplot('x*0-y',[-8,8])

hold off

grid on

%Аналітичний метод

syms x

y0='exp(-x)- x'

y=solve(y0,x)

y0=subs(y)

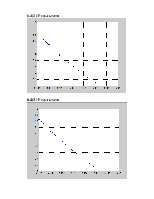
3.4 Результат

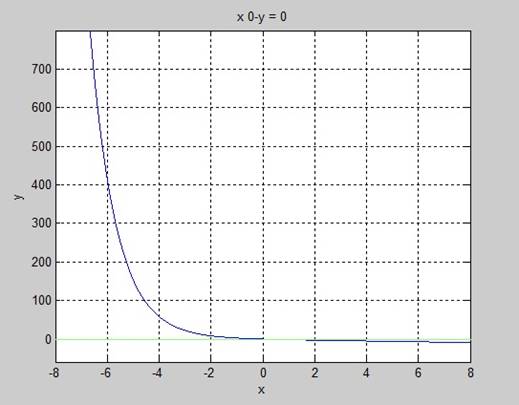
y0 = exp(-x)- x

y =exp(.26987413757344922387738245114716)

y0 = 0.5671

4.1 Вирішити систему нелінійних рівнянь графічним та аналітичним методом

4.2 Короткі теоретичні відомості

В загальному випадку система з n нелінійних рівнянь з n невідомими подається у вигляді:

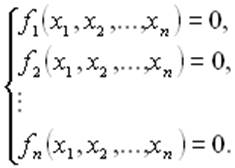
4.3 Програма

%x=sin(x)+sin(y)-1=0

%y=x^2-y ^2-1=0

clc

clear all

%Гафічний метод

ezplot(' sin(x)+sin(y)-1-x',[-8,8],[-8,8])

hold on

ezplot('x^2-y ^2-1-y',[-8,8],[-8,8])

hold off

grid on

%Аналітичний метод

syms x y

y=solve(' sin(x)+sin(y)-1-x','x^2-y ^2-1-y',x,y)

x0=subs(y.x)

y0=subs(y.y)

4.4 Результат

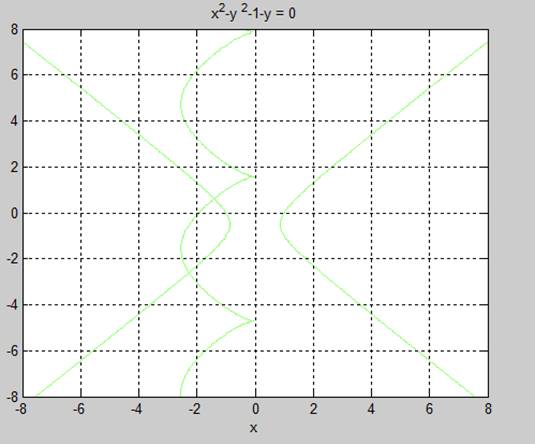
y =

x: [1x1 sym]

y: [1x1 sym]

x0 =

-1.4111

y0 =

0.6141

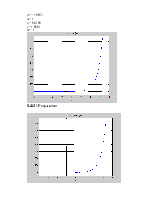
5.1 Знайти мінімум функції методом перебору та дихотомії(половинного поділу)

5.2 Короткі теоретичні відомості

Метод перебору (метод рівномірного пошуку) - найпростіший з методів пошуку значень дійсно-значних функцій за будь-яким із критеріїв порівняння (на максимум, на мінімум, на певну константу). Стосовно до екстремальних задач є прикладом прямого методу умовної одномірної пасивної оптимізації.

Дихотомія - роздвоєність, послідовне поділ на дві частини, не пов'язані між собою. Дихотомічне розподіл у математиці, філософії, логіці і лінгвістиці є способом освіти взаємовиключних підрозділів одного поняття або терміна і служить для утворення класифікації елементів.

5.3(1) Програма

%f(x)=e^x-sin(x) a=0 b=1

%f(x,y)=e^(y^2-x)+e^x

%Метод перебору

clc

clear all

a=0

b=1

step=0.1

y1=exp(a)-sin(x)

ezplot('exp(x)-sin(x)',[-8,8])

grid on

n=0

hold on

x=a

while x<b

x=x+step

y2=exp(x)-sin(x)

n=n+1

plot(x,y2,'o')

if(y2>y1)

x=x*step

y=exp(x)-sin(x)

break

end

y1=y2

end

hold off

5.3(2) Програма

clc

clear all

%Метод дихотомії

a=-0.5

b=0.5

E=0.001

y1=exp(a)+1/a

ezplot('exp(x)+1/x',[-8,8])

n=0

grid on

hold on

while (abs(b-a)>E)

L=b-a

x0=a+L/2

x1=a+L/4

x2=b-L/4

y0=exp(x0)+1/x0

y1=exp(x1)+1/x1

y2=exp(x2)+1/x2

plot(x1,y1,'o')

plot(x2,y2,'x')

n=n+1

if(y1<y0 & y0<y2)

b=x2

else if(y1>y0 & y0>y2)

a=x1

else

a=x1

b=x2

end

x0=(x1+x2)/2

end

5.4(1) Результат

a =0

b = 1

step = 0.1000

y1 = 0.4354

n = 0

x =0

x = 0.1000

y2 = 1.0053

n = 1

x = 0.0100

y =1.0001

n = 1

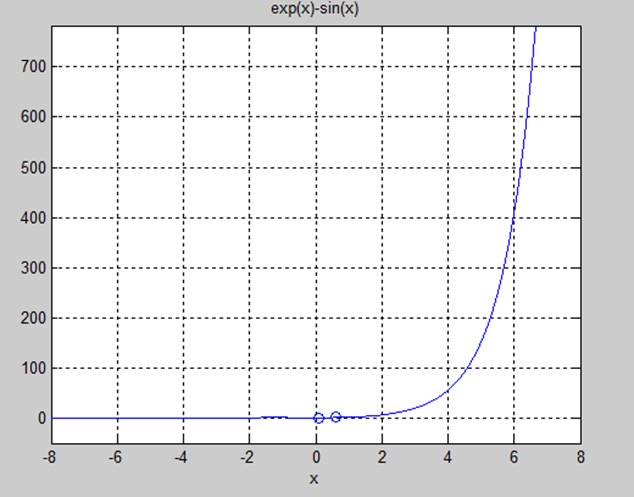
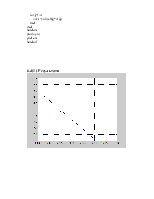
5.4(2) Результат

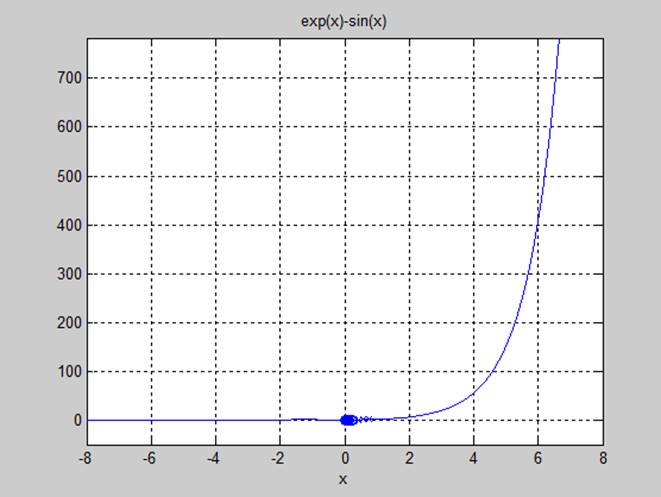
a =-1

b =1

E =0.001

y1 =1.0366

a =0.4882

b =0.4219

x0 =0

n =10

6.1 Знайти кубічну, квадратичну та лінійну апроксимацію заданих точок

6.2 Короткі теоретичні відомості

Для того щоб отримати аналітичні залежності, що описують великі масиви даних, використовують методи апроксимації, які основані на тому, що масив даних замінюють простою функцією (лінійною або квадратичною або кубічною або іншою), яка не обов’язково проходить через всі експериментальні точки, але описує тенденції зміни цих даних та забезпечує мінімум суми квадратів відхилень експериментальних даних від цією функції.

Апроксима́ція (лат. approximare — наближати) — наближене вираження одних математичних об'єктів іншими, простішими, наприклад, кривих ліній — ламаними,ірраціональних чисел — раціональними, неперервних функцій — многочленами.

6.3(1) Програма

clc

clear all

x=[0.115;0.120;0.125;0.130;0.135;0.140]

y=[8.65729;8.29329;7.95829;7.64893;7.36235;7.09613]

plot(x,y,'o')

for i=1:6

z(i,1)=1

z(i,2)=x(i)

end

b=inv(z'*z)*z'*y

for i=1:6

ya(i)=0

for j=1:2

ya(i)=ya(i)+b(j)*z(i,j)

end

hold on

plot(x,ya)

grid on

hold off

6.3(2) Програма

clc

clear all

x=[0.115;0.120;0.125;0.130;0.135;0.140]

y=[8.65729;8.29329;7.95829;7.64893;7.36235;7.09613]

plot(x,y,'o')

for i=1:6

z(i,1)=1

z(i,2)=x(i)

z(i,3)=x(i)^2

end

b=inv(z'*z)*z'*y

for i=1:6

ya(i)=0

for j=1:3

ya(i)=ya(i)+b(j)*z(i,j)

end

hold on

plot(x,ya)

grid on

hold off

6.3(3) Програма

clc

clear all

x=[0.115;0.120;0.125;0.130;0.135;0.140]

y=[8.65729;8.29329;7.95829;7.64893;7.36235;7.09613]

plot(x,y,'o')

for i=1:6

z(i,1)=1

z(i,2)=x(i)

z(i,3)=x(i)^2

z(i,4)=x(i)^3

end

b=inv(z'*z)*z'*y

for i=1:6

ya(i)=0

for j=1:4

ya(i)=ya(i)+b(j)*z(i,j)

end

hold on

plot(x,ya)

grid on

hold off

6.4(1) Результати

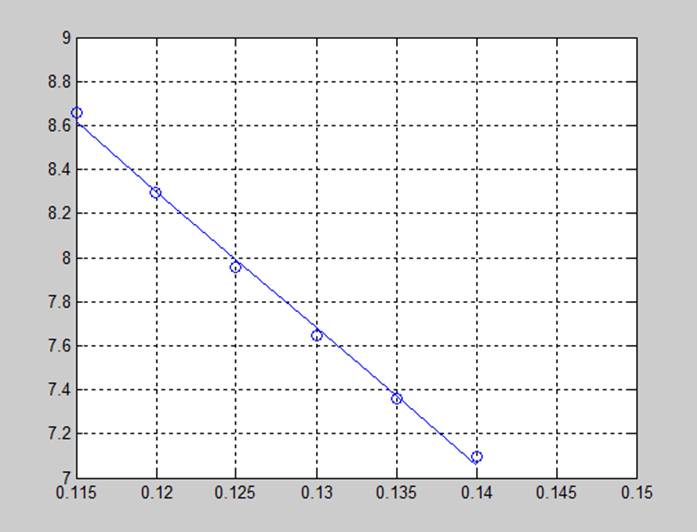
6.4(2) Результати

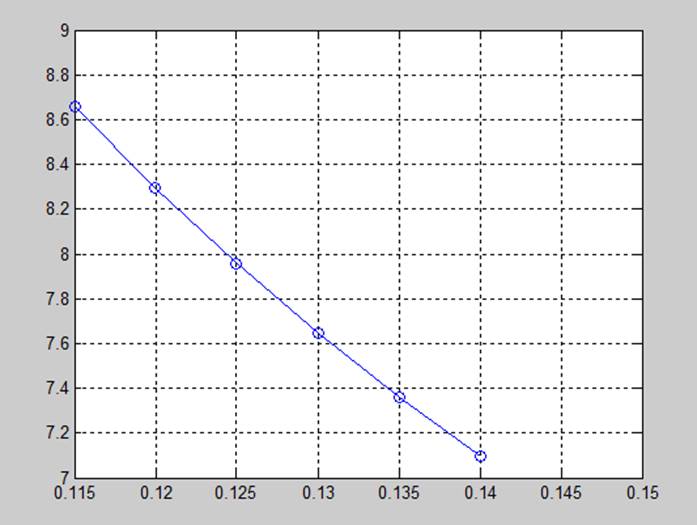
6.4(3) Результати

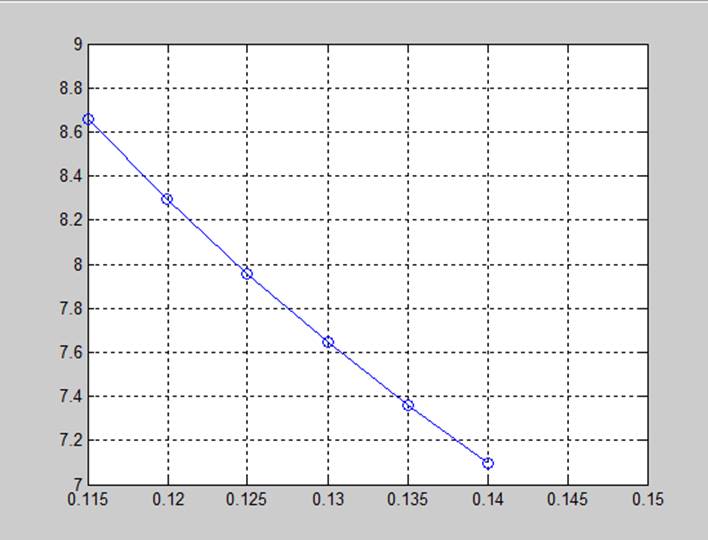
7.1 Знайти похідну функції в точці, використовуючи Matlab

7.2 Короткі теоретичні відомості

Похідна́— основне поняття диференційного числення, що характеризує швидкість зміни функції. Визначається як границявідношення приросту функції до приросту її аргументу коли приріст гументу прямує до нуля (якщо така границя існує). Функцію, що має скінченну похідну, називають диференційовною.

Нехай в деякому околі точки x₀ визначена функція f. Якщо ми візьмемо довільне число x в цьому околі, то приріст аргументу (позначається Δx) в цьому випадку визначається, як x−x₀, а приріст функції (Δy) — як f(x)−f(x₀). Тоді, якщо існує границя $\lim_{\Delta x\rightarrow 0}{\frac{\Delta y}{\Delta x}}$ , то вона називається похідною функції

Информация о работе

ВУЗ:

Неизвестный ВУЗ (НВ)

Предмет:

Информатика

Тип:

Задания на курсовые работы

Категория:

Информатика и выч. техника (Технические предметы)

Размер файла:

293 Kb

Скачали:

Скачать файл

Вирішити СЛАР. Робота з матрицями. Нелінійне рівняння графічним та аналітичним методом

Страницы работы

Фрагмент текста работы

Похожие материалы

Информация о работе