Выбор стандартной посадки по наибольшему натягу. Анализ выбранной посадки с натягом

Задача 2

1.   Рассчитать и выбрать посадку с натягом для соединения зубчатого колеса с валом (рис. 2.1).

2.   Выполнить анализ полученной посадки и построить схему расположения полей допусков.

3.      Обозначить посадку соединения и поля допусков сопрягаемых деталей на эскизах.

Таблица 1 – Исходные данные

Диаметр соединения вала, d, мм	150
Диаметр впадин зубчатого колеса,	300
Длина соединения вала и зубчатого колеса, L, мм	250
Крутящий момент,	12000
Шероховатость поверхности вала,	6,3
Шероховатость поверхности зубчатого колеса,	6,3
Марка стали	45
Предел текучести,  Па	36·107

Таблица 2 – Основные данные для расчёта

Название и размерность параметра вала и колеса	Вал	Зубчатое колесо
Длина соединения L, мм Диаметр соединения (вала и отверстия ступицы), мм	L = 120 d = D = 150
Диаметр впадин зубчатого колеса, мм Модуль упругости, Па (Н/ м2) Предел текучести, Па (Н/ м2) Коэффициент Пуассона μ Шероховатость поверхности, мкм	Ed = 2,06 · 1011 σT = 36 · 107 μd = 0,3 Rzd = 6,3	d2 = 300 ED = 2,06 · 1011 σT = 36 · 107 μD = 0,3 RzD = 6,3

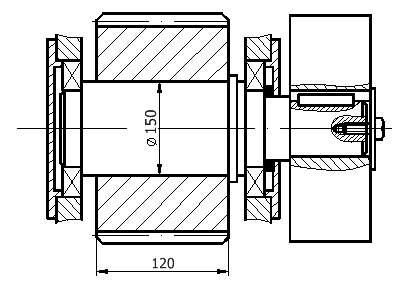
Рисунок 1 – Общий вид вала в сборе

Расчёт функциональных натягов

Используя один из методов расчёта посадок с натягом [1, 3, 4, 5] и др., вычисляем значения наименьшего расчётного натяга, обеспечивающего взаимную неподвижность соединяемых деталей, и наибольшего расчётного натяга, определяющего прочность соединяемых деталей.

Натяги N_min и N_max, обеспечиваемые стандартной посадкой, должны удовлетворять условиям:

N_minф < N_min, N_maxф > N_max.

Значение наименьшего расчётного натяга определяется по формуле, мкм:

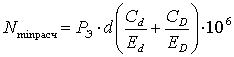,                                        (2.1)

где Р_Э – удельное контактное эксплуатационное давление при действии крутящего момента, Па:

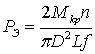,                                                    (2.2)

где f – коэффициент трения, f = 0,15;

n – коэффициент запаса прочности соединения, n = 1,5 – 2;

D = d – номинальный диаметр соединения, м;

L – длина соединения, м.

 Па

C_D и C_d – коэффициенты Ламэ:

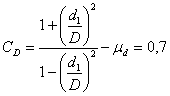                                                 (2.3)

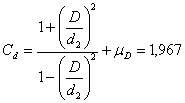                                                (2.4)

где d₁ – внутренний диаметр вала (если вал полый), м. В нашем случае d₁ = 0;

d₂ – наружный диаметр втулки или впадин зубчатого колеса, м.

Подставляя полученные значения величин в (2.1), получим:

N_{min расч}  = 54,968 мкм;

Наибольший расчётный натяг определяется по формуле, мкм:

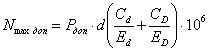,                               (2.5)

где Р_доп – наибольшее допускаемое давление на поверхности вала или втулки, Па:

на поверхности втулки отсутствуют пластические деформации при

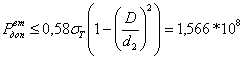                            (2.6)

на поверхности вала отсутствуют пластические деформации при

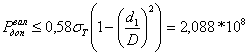                              (2.7)

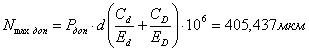
Исходя из наименьшего допускаемого давления Р_доп, получим (2.5) максимальный расчётный натяг N_{max расч}  = 405,437 мкм.

Находим поправку к расчетному натягу на смятие неровностей поверхности детали U_Rz, остальные поправки можно принять равными нулю [1, 3, 4].

 мкм, где k – коэффициент, учитывающий высоту смятия неровностей отверстия втулки и вала (табл. 3). Для принятого метода сборки (с нагревом зубчатого колеса) принимаем k = 0,5.

Таблица 3

Метод сборки соединения		k
Механическая запрессовка при нормальной температуре	без смазочного материала	0,25 – 0,5
	со смазочным материалом	0,25 – 0,35
С нагревом охватывающей детали		0,4 – 0,5
С охлаждением вала		0,6 – 0,7

С учетом поправки величины граничных допустимых значений функциональных натягов для выбора посадки будут равны:

 мкм,

 мкм.

Схема расположения полей допусков посадки с натягом в системе отверстия, используемая для выбора стандартной посадки, представлена на рис. 2.2. Нижнее отклонение основного отверстия EI = 0.

Рис. 2.2. Схема расположения полей допусков

посадки с натягом в системе отверстия

Выбор стандартной посадки по наибольшему натягу.

Исходя из условия, что натяг, обеспечиваемый стандартной посадкой (ГОСТ 25347-82), должен быть меньше функционального (см. рис. 2.2):

(N_max = es – EI) < N_{max ф} ,

определяем наибольшее допустимое значение верхнего отклонения вала:

es < N_{max ф} - EI = 418,037 - 0 = 418,037 мкм.                     (2.8)

В табл. 1 приложения приведены рекомендуемые ГОСТ 25347-82 посадки в системе отверстия. При изготовлении отверстия по седьмому (Н7) или по восьмому (Н8) квалитету для получения натяга используются поля допусков валов:

для Н7 – p6, r6, s6, s7, t6, u7 (посадки H7/p6, H7/r6, H7/s6, H7/s7, H7/t6, H7/u7);

для H8 – s7, u8, x8, z8 (посадки H8/s7, H8/u8, H8/x8, H8/z8).

Выбрав отклонения, соответствующие этим полям допусков по табл. 2 приложения (ГОСТ 25347-82) или по [4, 6, 8] и др., проверяем выполнение неравенства (2.8) по величине верхнего отклонения вала для рассматриваемых полей допусков валов. Например

150u8: es = +253 мкм < (429,3 мкм = N_{max ф}).

Принимаем поле допуска 150u8 (es = +253 мкм, ei = +190 мкм), так как в этом случае неравенство (2.8) выполняется (рис. 2.3).

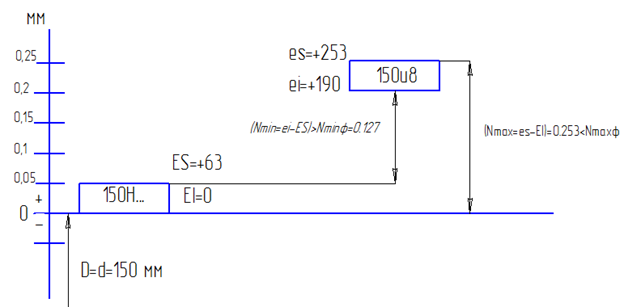
Рис. 2.3. Схема расположения полей допусков посадки

с натягом с валом 150u8

Исходя из условия (N_min = ei – ES) > N_{min ф}, определяем наибольшее допустимое значение верхнего отклонения основного отверстия:

ES < ei - N_{min ф} = +190 – 67,568 = 122,432 мкм.                      (2.9)

Определяем верхние отклонения полей допусков основных отверстий по табл. 3 приложения (ГОСТ 25347-82). Из полученных отклонений выбираем отклонения, обеспечивающие выполнение неравенства (2.9):

150 Н8:         ES = + 72 < 91 мкм - неравенство выполняется;

Принимаем поле допуска 150Н8 (ES = +63 мкм; EI = 0) и рекомендуемую