Автоматизация. Автоматические и автоматизированные САУ. Классификация систем, страница 3

В таких системах УУ стремиться ликвидировать все отклонения вых. величин от его значения, определяемого заданием входной, включая все изменения параметров системы и учитывая все возмущающие воздействия. Такие системы обеспечивают точность управления. Для точного управления необходимо скомпенсировать все возмущения, действующие на систему. Для этого в систему включают столько датчиков, сколько на неё действует возмущающих воздействий. В этом случае сист. получается сложной и массивной. Проще построить систему на основе принципа обратной связи. В этом случае выходная величина сравнивается с заданной и формируется отклонение

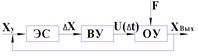
Дифференциальная чувствительность звеньев.

Производная выходной координаты по входной, характеризующая угол наклона касательной к статической характеристике называется дифференциальной чувствительностью звена: (1)

Формула (1) справедлива для линейных звеньев. При нелинейной статической характеристике дифференциальная чувствительность – величина переменная, поэтому используют понятие средней диф. чувствительности (2), где  - угол наклона касательной к линиаризированной статической характеристике. У релейного звена на вертикальном участке диф. чувств. равна нулю, на горизонтальном участке равна . В этом случае используют понятие коэффициента управления (3).

Последовательное соединение звеньев

 ; (4)

Параллельное соединение звеньев

          

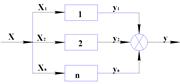
Встречно-параллельное соединение звеньев

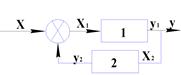
                                  (6)

+ - положит обр. св.

– - отр. обр. св.

Приведение уравнений к безразмерной форме

В статическом режиме поведения звена описывается статич. коэффициентом . Для сравнения характера преобразования в звеньях разной природы применяют относительный коэф. . В динамике поведение системы описывается выражением

(1)

В этом уравнении все переменные являются размерными величинами. У систем разной природы эти величины имеют разные параметры. Однако форма записи у разных систем может быть одинаковой. С этой целью уравнение (1) приводится к безразмерной форме, а все величины характеризуются относительными изменениями. Для точки с координатами  относительное изменение запишется в виде:

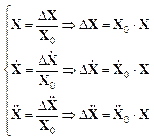(2)

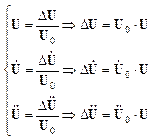(3)

Подставим выражение (2) и (3) в выражение (1)

(4)

Разделим выражение (4) на выражение , получим

(5)

Введём замену:

; ; ; ;

Получим:

 (6)

Уравнение (6) связывает относительное изменение переменных, которые являются безразмерными. В такой форме уравнение (6) применимо к системам любой природы: механические, гидравлические, электрические.

Преобразование Лапласа и его свойства.

(1)

Соотношение (1), по которому функция  вещественной переменной t ставится в соотношение функции  комплексной переменной S называется преобразованием Лапласа.

(2)

L – Оператор Лапласа

Функция оригинала должна обладать свойствами:

1. должна быть определена на всей положительной полуоси, непрерывна и кусочно-дифференцируема.

2. Должно выполняться условие при  

3. Должны существовать такие положительные числа, для которых выполняется условие

Обратный переход от изображения к оригиналу.

(3)

Свойство Лапласа

1.  Свойство линейности

2.  Изображение производной

3.  Изображение интеграла

4.  Теорема запаздывания

5.  Теорема о свёртке

6.   Свойство о предельных переходах

7.  Теорема разложения

Передаточные функции в изображениях по Лапласу

(1)

Выражение (1) – линейная комбин. функция, поэтому для него справедливо 1-ое свойство преобразования Лапласа.

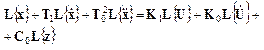(2)

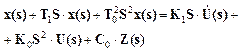(3)

Пусть , то

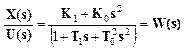(5)

 - передаточная функция в изображении по Лапласу

Существует формальное правило: для получения передаточной функции по Лапласу достаточно заменить p на S.

S – Комплексная переменная.

, при U=0

(6)

Таким образом, можно получить уравнение системы в изображении по Лапласу.

(7)

Вывод уравнений звеньев автоматически.

Рассмотрим силовые отношения для механического звена с выходной координатой в виде перемещения.

 

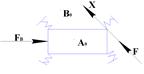
Пусть в пространстве звено закреплено спец. образом на пружинных растяжках.

т. - центр масс звена

Положение т.  определяется:

1)  Массой пружины

2)  Жесткость пружины

3)  Количество и пространственное положение пружин

Любая конструкция и расположение пружин в пространстве обеспечивает как минимум одну устойчивую точку в которой звено находится в покое. Если в некоторый момент времени воздействовать на звено силой F, в направлении x, то выходная координата звена не  будет равна равновесной .

Центр масс переместится в точку  и главный вектор сил действующих на звено будет равен 0.

Равнодействующая сила стремящаяся вернуть звено в установившееся состояние называется восстанавливающей функцией звена .

(Чтобы вернулось в прежнее состояние)

В общем случае восстанавливающая сила связана с координатами x и y.

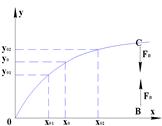
Для точки  лежащей на равновесной характеристики восстанавливающая сила равна 0.

Для точки B у которой координата  восстанавливающая сила больше 0. Для точки C у которой  восстанавливающая сила меньше нуля.

Если изменять начальное условие, то равновесное положение звена будет другим. Бесконечно изменяя факторы (1,2,3) можно получить геометрическое место точек равновесного положения звена или кривую устойчивости. При снятии возмущающей силы звено устремиться в исходное положение каким-либо неизвестным способом. Необходимо вывести диф. уравнение движения звена, решить его и получить условие при котором звено возвращается в исходное состояние необходимым образом. Обозначим m – масса частей звена. Уравнение движения звена опишется вторым законом Ньютона. (1), где

 - Восстанавливающая сила  - Сила сопротивления

(2) - сила вязкого трения

(3) Исходное уравнение движения звена

Введем отклонение от устойчивого положения:

;; ; ; , где

x, y – текущее значение

x – входы, y – выходы координаты

,  - отклонения текущего значения

, - значения координат равновесного состояния

Разложим восстанавливающую силу в ряд Тейлора как функцию двух переменных

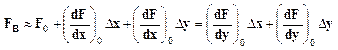(4)

Перепишем уравнение (3) с учетом (4)

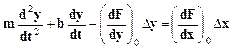(5)

Пусть ; ; ; ; ; ;

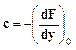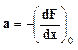
Перепишем (5) с учетом обозначений (6)

Коэффициент при второй производной выходной координаты имеет размерность время в квадрате, коэффициент при безразмерной выходной координате является безразмерной.

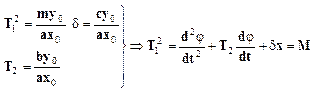(7)

Выражение (7) линеаризованное уравнение звена второго порядка  - постоянная времени  характеризующая инерционность звена, численно равна половине квадрата времени необходимого для перемещения звена от исходного предельного до равновесного положения, при максимальной восстанавливающей силе и отсутствии сопротивления.