Методы теории оценивания в задачах идентификации. Байесовские оценки. Оптимальная оценка для квадратичной функции потерь

ГЛАВА 5.

МЕТОДЫ ТЕОРИИ ОЦЕНИВАНИЯ В ЗАДАЧАХ ИДЕНТИФИКАЦИИ.

5.1 Постановка задачи

Под оцениванием обычно понимают процесс определения подходящих, в определенном смысле, значений неизвестных параметров на основе имеющейся информации, связанной с процессом измерения других, доступных наблюдению параметров.

Оцениваемые параметры могут быть по своей природе как случайными, так и неслучайными. В силу случайности характера ошибок измерения доступных наблюдению параметров, эти параметры во всех случаях являются случайными величинами. Поскольку любая оценка является функцией от наблюдаемых величин, то она также является случайной.

Принято оценки, характеризующиеся числовыми значениями, называть точечными, а оценки, характеризующиеся принадлежностью параметра некоторому интервалу с заданной вероятностью - интервальными.

Оценки, являющиеся линейными комбинациями измерений, называются линейными, в противном случае - нелинейными.

5.2 Байесовские оценки

Пусть  x - истинное значение оцениваемого параметра,

 - оценка этого параметра, тогда ошибка оценивания определяется следующим образом:

                                                                              (5.2.1)

За наличие ошибки оценивания вводится штраф, определяемый функцией потерь

, которая должна обладать подходящими свойствами, а именно:

1.   L(0)=0 - отсутствие штрафа при отсутствии ошибки;

2.    - условие симметрии;

3.    - условие монотонности, выполняемое при  при

В основе теории байесовского оценивания лежит предположение о наиболее полном объеме априорной информации об оцениваемом векторе, а именно: если

х=[х₁, х₂, ..., х_n]^Т - вектор оцениваемых параметров,

v=[v₁, ..., v_r]^T - вектор ошибок измерения, то управление наблюдения имеет вид:

,

где - известное преобразование.

Тогда f(x) - априорная плотность распределения вероятности (ПРВ) оцениваемого параметра, характеризующая степень неопределенности его возможных значений, предполагается известной. Известна также условная плотность f(z/x) распределения вероятности вектора наблюдений.

Тогда для реализовавшегося значения оценки  потери  будут зависеть от истинного значения х, которое случайно и, следовательно, сама величина  случайная. Средние возможные потери, которые связаны с выбором , можно получить усреднением величины  по всем возможным значениям истинных значений х, имеющих распределение f(x), а именно:

                                                       (5.2.2)

Оценка, минимизирующая величину критерия (5.2.2), называется байесовской, соответствующей априорной вероятности f(x).

В выражении (5.2.2) отсутствуют явно результаты наблюдений, поэтому удобно перейти к другой форме средних потерь, содержащей эти наблюдения.

Пусть z^* - фиксированный набор результатов наблюдений, тогда f(x/z^*) - апостериорная плотность распределения вероятностей вектора х, связанная с появлением вектора z^* , а величина

                                                     (5.2.3)

представляет собой средние условные потери, при условии, что z^*- фиксировано. Усреднение величины (5.2.3) по множеству всех возможных результатов наблюдения z приводит к средним потерям, или байесовскому риску

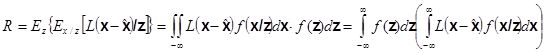               (5.2.4)

Из выражения (5.2.4) следует в силу положительности f(z), что если оценка  минимизирует средние условные потери при любом фиксированном значении z^*, то она минимизирует и средние потери R, т.е.

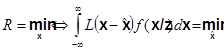                                                        (5.2.5)

Любую оценку , минимизирующую байесовский риск R, принято называть оптимальной оценкой в классе Q, соответствующей данной функции потерь. Важно отметить, что поскольку f(x/z) содержит всю информацию об оцениваемом векторе x, содержащуюся в наблюдаемом z, то характер оптимальных оценок будет зависеть как от вида функции потерь, так и от класса оценок Q (линейные, нелинейные и т.д.).

Наибольшее распространение получили следующие функции потерь:

1.   , где ,  - квадратичная функция потерь (рис.5.2.1).

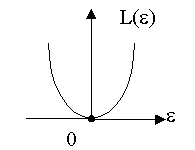
Рис.5.2.1

2.   , ,  - модульная функция потерь (рис.5.2.2)

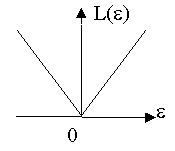
Рис.5.2.2

3. 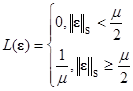   - простая функция потерь (рис.5.2.3)

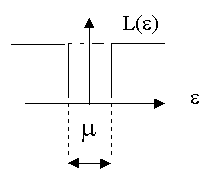
Рис.5.2.3

Определим конкретный вид оценок для квадратичной функции потерь в классе всех возможных оценок, в том числе и нелинейных.

5.3 Оптимальная оценка для квадратичной функции потерь

Итак, пусть

, где G – положительно определённая симметричная весовая матрица