Интерполяция функций одной переменной. Интерполяционный многочлен Лагранжа. Аппроксимирующие сплайны (B-сплайны)

ЗАДАНИЕ № 2

Интерполяция функций одной переменной

Задача интерполяции возникает в случае, когда функция f(x) задана табличным (дискретным) способом, т.е. когда в точках , называемых узлами таблицы, заданы значения функции  и требуется определить ее значение (приближенное) при значениях аргумента, не совпадающих с узлами таблицы. Понятно, что в общем случае такая задача не имеет единственного решения и для ее приближенного решения приходится вводить определенные предположения.

1. Интерполяционный многочлен Лагранжа.

Если предположить, что таблично заданная функция может быть приближена многочленом степени n, то при выполнении условий интерполяции, т.е. совпадения значений искомого многочлена со значениями таблично заданной функции в узлах таблицы, можно построить единственный многочлен, называемый многочленом Лагранжа:

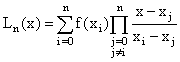                                                  .                                                        (1)

При этом погрешность интерполяции оценивается как

,                                 (2)

где  для всех .

Если в качестве узлов интерполяции выбрать корни многочленов Чебышева

,                                                      (3)

где  - границы отрезка, на котором заданы значения функции , причем значения и  не совпадают с границами отрезка, то погрешность интерполяции будет минимальной, поскольку в этом случае многочлен  в (2) будет многочленом Чебышева  со старшим коэффициентом, равным единице, т.е. многочленом, наименее уклоняющимся от нуля на заданном интервале. В этом случае оценка максимальной погрешности интерполяции (2) будет следующей:

Задание

Для гладкой (аналитической) функции, имеющей ограниченную производную порядка  на некотором отрезке  (например, для ) вычислить таблицу ее значений с равномерным расположением узлов  для ряда заданных узлов  n (например, n =  5; 10; 20), т.е. для .   Для полинома Лагранжа построить графики приближенной (2) и точной погрешностей  (при выводе графиков на экран использовать в интервале [a,b] не менее 100 точек). При вычислении приближенной погрешности по формуле (2) возникают проблемы, связанные  с вычислением факториала  при больших значениях n. Поэтому вместо (2) следует использовать эквивалентную ей формулу

                                                                                                         (4)

Сравнить поведение точной и приближенной погрешностей и объяснить, почему   превышает .

1.2. Для выбранной функции на том же отрезке построить таблицу ее значений, выбрав в качестве  узлов интерполяции корни полиномов Чебышева (3). Сравнить поведение погрешностей и  в этом случае.

1.3. Исследовать поведение точной  погрешности   для «зашумленной» таблично заданной функции  на интервале  для значений n = 5, 10, 20 в случае равномерного расположения узлов и в случае выбора в качестве узлов корней полиномов Чебышева. Убедитесь, что в последнем случае погрешность интерполяции оказывается существенно меньше.

2. Кубический сплайн

Отрезок интерполяции  разбивается на N подинтервалов , на каждом из которых строится кубический полином:

,                                       (5)

В узлах интерполяции выполняются равенства , , которые дают N + 1 условие. Еще 3(N - 1) условий дают условия гладкого сопряжения во внутренних узлах интерполяции

.

Недостающие два условия задаются на концах отрезка интерполяции в точках  и . Здесь могут быть заданы либо первая, либо вторая производные сплайн-функции, либо их линейные комбинации.

Тогда для определения коэффициентов сплайна имеет место следующая система уравнений

                                   (6)

, где .

Из последнего уравнения системы (6) выразим :

                                                                   (7)

Здесь несуществующий коэффициент  используется при задании граничного условия.

Из второго уравнения системы (6) выразим :

                                    (8)

Подставляя выражения для , и выражение (8) для  в третье уравнение системы (6), получим одно уравнение, связывающее значение коэффициента   в трех соседних точках. Сдвигая индекс n на единицу, запишем систему линейных алгебраических уравнений для определения коэффициентов в следующем виде

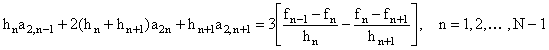,           (9)

Необходимые для замыкания системы (9) значения коэффициентов  и определяются из граничных условий. Рассмотрим два случая граничных условий.

1). На концах интервала заданы значения второй производной сплайна

  . Тогда из (6)

.                                                                    (10)

где  - значения вторых производных на левой и правой границах интервала соответственно.

2). На концах интервала заданы значения первой производной сплайна  и   :

  .                   (11)

где  - значения первых производных на левой и правой границах интервала соответственно.

Запишем систему (9) в следующем общем виде с трехдиагональной матрицей

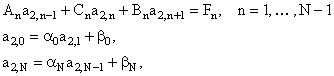                                         (12)

где , .

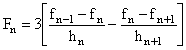В случае граничных условий (10)     ,  в случае (11)

, .

Для решения системы (12) используется метод прогонки. На первом этапе (прямая прогонка) по рекуррентным формулам вычисляются т.н. прогоночные коэффициенты