Пример. Уточним описание предлагаемого алгоритма на конкретном примере. Пусть
Каждая строкаbi матрицы В, обладающая k единицами, порождает k требований, представляемых соответствующими столбцами матрицы R, получаемыми из вектораbi путем замены всех нулей на «—», а всех единиц, кроме одной, на нуль. Например, первая строка матрицы В порождает два требования, предъявляемые к матрице X:в матрице Х должен существовать столбецхi со значениями компонент хai = 1 и xbi = 0 и должен существовать столбецхj со значениями компонент хaj = 0 и xbj = 1. Представив эти требования троичными векторами 10 — — — и 0 1 — — —, мы найдем тем самым первые два столбца матрицы R. Аналогично определяются и остальные столбцы, в результате чего получаем
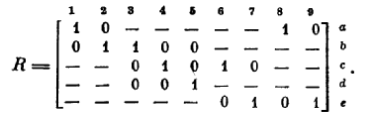
Матрица Х удовлетворит всем предъявляемым к ней требованиям, если для каждого столбца матрицы R найдется неортогональный ему столбец в матрице X. Очевидно, что один и тот же столбец из Х может удовлетворить нескольким требованиям, представляемым некоторым подмножеством столбцов из R. Необходимым и достаточным условием возможности построения такого столбца является взаимная попарная неортогональность столбцов из данного подмножества. Поэтому задача отыскания матрицы Х с минимальным числом столбцов сводится к разбиению множества столбцов матрицы R на минимальное число классов, образуемых взаимно неортогональными столбцами. В свою очередь эта задача сводится к уже знакомой читателю задаче раскраски графа, точнее к такой раскраске вершин некоторого графа в минимальное число цветов, при которой любые две соседние (соединенные ребром) вершины окажутся окрашенными в различные цвета. В данном случае вершины раскрашиваемого графа будут представлять столбцы матрицы R, а ребрами будет задано отношение несовместимости столбцов — будем полагать столбцы несовместимыми, если они ортогональны.
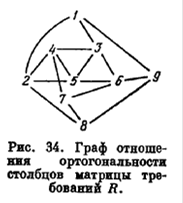 |
Описанный граф, соответствующий рассматриваемому примеру, показан на рис. 34.
Решив задачу минимальной раскраски, например путем сведения ее к задаче о кратчайшем покрытии (находятся все максимальные группы попарно совместимых столбцов, строится булева матрица бинарного отношения принадлежности столбцов матрицы R этим максимальным группам и находится кратчайшее покрытие этой матрицы), мы получим точное решение поставленной задачи, точнее говоря, одно из них, поскольку решение задачи о кратчайшем покрытии в общем случае не однозначно. Одно из таких решений задается разбиением {1, 4, 6, 8/ 2, З/ 5, 7, 9} множества столбцов матрицы R на три класса, порождающим трехстолбцовую матрицу X:
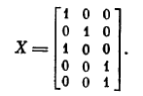
Каждый столбец этой матрицы представляет собой пересечение троичных векторов, задающих значения столбцов, образующих соответствующий класс. Если некоторая компонента вектора-результата примет при этом значение «—», мы доопределяем ее до нуля.
Вычислив по формуле У= ВXХ матрицу Y, представим полученный результат в целом, в виде своеобразного треугольника, удобного для проверки заданного преобразования:
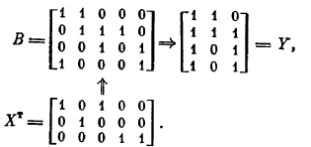
Интересно интерпретировать этот результат, выяснив, как же будут
опознаваться различные «неисправности» в матрице В. Оказывается, что
единицы этой матрицы связаны взаимно однозначным отношением с единицами мат
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.