 |
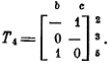 |
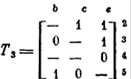
Согласно правилу 3 полагаем с = 0, а b = 1. Далее срабатывает правило возврата, поскольку матрица Т становится пустой после удаления столбцов.
Возвратившись к точке ветвления, полагаем теперь a = 0. Последующее редуцирование приводит к следующему значению переменной матрицы Т:
 |
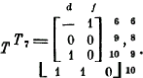 |
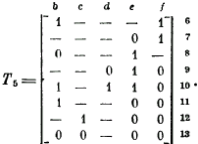
Далее по правилу 3 компонента b получает значение 1 и матрица Т сокращается до затем следует выбор значения 0 для компоненты f и получение остатка
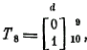 |
|
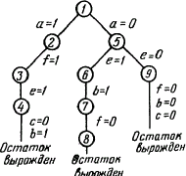
Рис. 19. Дерево поиска ортогонального вектора. |
который оказывается вырожденным: компонента d должна получить одновременно значения 0 и 1, что невозможно. Опять срабатывает правило возврата.
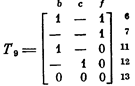
Рассмотрим теперь оставшийся вариант, положив е = 0. Здесь мы должны найти вектор, оротогональный матрице
 |
 |
||
В соответствии с правилом 3, мы должны последовательно выбрать значения f = О, b = 0 и с = О, после чего становится очевидным, что мы не можем сделать вектор w ортогональным строке 13.
Этим завершается перебор значений вектора w с целью нахождения ортогонального вектора v и устанавливается отсутствие последнего, т. е. доказывается тем самым вырожденность заданной матрицы U.
Описанная последовательность рассуждений отображается в более сжатом виде деревом поиска, показанным на рис. 19. Как видно, дерево оказывается довольно простым и имеет лишь две точки ветвления. Нумерация вершин отражает порядок рассмотрения промежуточных ситуаций: используются те же номера, что и в обозначениях соответствующих значений переменной матрицы Т. На рисунке приведена также информация о выбираемых значениях компонент вектора w.
6. Задачи о покрытии множеств
Решение ряда логических задач сводится к рассмотрению некоторых конечных множеств и поиску в них подмножеств с заданными свойствами. Часто поиск сопровождается оценкой качества подмножеств и в этом случае требуется находить такие подмножества, которые, удовлетворяя заданным требованиям, обладали бы наивысшим качеством. Иногда требуется находить все такие подмножества, иногда достаточно найти одно из них. Естественно, что в последнем случае объем вычислений может быть меньше.
Зачастую оказывается, что множество решений — подмножеств с заданными свойствами — является выпуклым по отношению включения, и это означает, что если некоторое подмножество является решением, то и любое его расширение, получаемое добавлением в подмножество некоторых новых элементов, также будет представлять собой решение. В таком случае нахождение множества всех решений сводится к нахождению его нижней границы, что может иногда существенно сократить объем производимых при поиске вычислений. Хорошим примером к этому может послужить следующая задача.
Нахождение всех покрытий множества. Пусть заданы множество А и множество В, причем элементами последнего служат некоторые подмножества из первого и В является покрытием множества А, что означает следующее: объединение всех элементов из В, т. в. соответствующих подмножеств из А, равно множеству А. Требуется найти все покрытия множества А, составленные из элементов множества В.
Выпуклость множества всех покрытий очевидна: действительно, если некоторое подмножество из В является покрытием, то, добавив к нему некоторый новый элемент из В, мы получим опять-таки покрытие, в силу свойств теоретико-множественной операции объединения.
Если же мы будем удалять из покрытия некоторые его элементы, мы сможет полудить такое подмножество из множества В, которое уже не является покрытием. Множество всех покрытий имеет нижнюю границу, образованную простыми покрытиями, т. е. такими подмножествами из В, которые являются покрытиями, но перестают быть ими при удалении любого элемента. Множество простых покрытий задает таким образом множество всех покрытий, поэтому при решении сформулированной задачи в целом можно ограничиться нахождением именно простых покрытий. Это в какой-то степени упрощает задачу, поскольку перебор подмножеств из В, производимый при поиске простых покрытий, можно ограничить некоторой окрестностью нижней границы множества всех покрытий.
Покажем, как это делается, на примере конкретных множеств А и В, используя для их представления булеву матрицу С, строки которой сi , поставлены в соответствие элементам ai множества A, а столбцы сj представляют (единицами) те подмножества из А, которые служат элементами bj множества В. При таком представлении данных задача может быть переформулирована в задачу нахождения всех простых столбцовых покрытий булевой матрицы С. Действительно, покрытие множества А будет в этом случае представляться подмножеством столбцов из С, содержащих сообща не менее одной единицы в каждой из строк матрицы С. Если это свойство подмножества утрачивается при удалении любого столбца, покрытие оказывается простым.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.