Классические методы минимизации булевых функций. Сжатие булевой матрицы, страница 2

Сформулированная задача решается довольно просто. Если в матрице B существует некоторая пара строк b_i и b_j, находящихся в отношении поглощения b_i ³ b_j (неравенство выполняется покомпонентно), то строку b_i  (поглощающую) можно выбросить из матрицы B, поскольку соответствующие строки u_i и u_j матрицы U будут представлять интервалы, находящиеся в отношении включения, и, следовательно, удаление первого из них не приведет к изменению характеристического множества М¹ реализуемой булевой функции f  ¾ результата    объединения всех интервалов, представленных матрицей U.

Если же в матрице В не существует пары строк с указанным свойством, то эта матрица не может быть упрощена и вообще не существует более простой матрицы, порождающей эквивалентный оператор типа \/В^. Дело в том, что в этом случае каждая из строк матрицы В представляет собой элемент множества М¹, принадлежащий лишь одному максимальному интервалу из М¹, а именно тому, который представлен соответствующей строкой матрицы U. Поэтому каждый из интервалов, заданных матрицей U, необходимо включить в решение, а это и означает, что матрица U неупрощаема, так же как и матрица В.

В рассматриваемом примере матрица В оказывается неупрощаемой.

З а д а ч а   м и н и м и з а ц и и   Д Н Ф. В то время как составные операторы типа ÚB^ реализуют лишь монотонные булевы функции, оператор ÚT^D может реализовать любую булеву функцию. Для этого достаточно выразить эту функцию в дизъюнктивной нормальной форме и представить последнюю структурной матрицей Т.

Действительно, где элементарная конъюнкция k_i задается строкой t_iматрицы Т  и  определяется по формуле

_                                                                           _  т. е. включает символ x_j, если t^j_i = 1, включает x_j, если t^j_i = 0,  и не включает ни x_j , ни x_j , если t^j_i = «—».

Пусть, например, нам известна следующая дизъюнктивная нормальная форма булевой функции f:

Представив эту ДНФ троичной матрицей

примем эту матрицу за структурную и построим соответствующую схему (рис. 40). Легко убедиться , что полученная таким образом схема реализует данную функцию f.

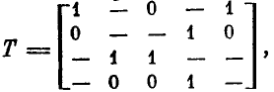Действительно,

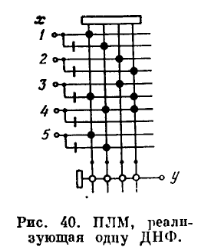Задача максимального упрощения оператора ÚT^D совпадает поэтому с задачей минимизации ДНФ булевой функции, причем в общем случае, когда мы не ограничиваемся, например, рассмотрением монотонных функций. Задача заключается в том, что требуется найти такую ДНФ для заданной булевой функции f, которая содержала бы минимальное  число  конъюнкции (кратчайшая ДНФ) или минимальное число букв (минимальная  ДНФ). Первой формулировке соответствует поиск некоторой троичной матрицы U с минимальным числом строк, второй — с минимальным числом единиц и нулей. При этом должно выполняться условие ÚT^D = ÚU^D.

Знакомство с методами минимизации ДНФ принято начинать с классических методов Квайна — МакКласки и Блека — Порецкого, описываемых практически в любом учебнике по теории автоматов. Мы ограничимся их кратким изложением в векторной интерпретации.

Общим для данных двух методов является то, что оба они основаны на предварительном получении множества всех простых импликант заданной булевой функции и последующем выделении из него некоторого подмножества, которое и будет представлять решение. Различаются эти методы способом нахождения простых импликант.

Простой импликднтой булевой функции f (x₁, x₂, … , x_n) называется такая элементарная конъюнкция k,  которая имплицирует функцию f  (имеется в виду  формальная   импликация k Þ f: функция f принимает значение 1 на любом наборе значений переменных x₁, x₂, … ,x_n,  на котором k = 1), но не будет ее имплицировать при удалении из k любого символа. Очевидно, что простые импликанты функции f соответствуют максимальным интервалам характеристического множества М¹ этой функции и что при поиске простейших ДНФ типа безызбыточных, когда из ДНФ нельзя (без нарушения представляемой функции) выбросить ни одного члена и ни одной буквы в члене, есть смысл ограничиться рассмотрением именно простых имлликант. Очевидно также, что задача минимизации ДНФ сводится к задаче нахождения оптимального интервального покрытия характеристического множества рассматриваемой булевой функции.