Производная неявной функции. Производная по направлению и градиент. Экстремум функции нескольких переменных

Производная неявной функции.

 - неявная (для двух переменных).                                                              (1)

Теорема: Пусть , т.е непрерывная функция  задается не явно, где , , - непрерывные функции в некоторой области D, содержащей точку , координаты которой удовлетворяют уравнению (1), и в которой , тогда .

Доказательство: Переменным x и y дадим приращение и  соответственно.

 - полное приращение функции F.

  | :

- бесконечно малые величины.

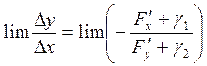
- производная от функции заданной неявно.

Пример:

- производные первого порядка.

- производные второго порядка

Определение: Частной производной n-го порядка, называется первая производная от производной  n-1 -го порядка.

Пример:

;

 и т.д.

Теорема: Если функция и ее частные производные  определены и непрерывны в некоторой точке М(х,у) и в некоторой ее окрестности то,  в точке М.

Производная по направлению и градиент.

Пусть функция  задана в некоторой области D.

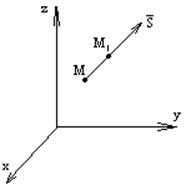Проведем из точки М вектор с направляющими косинусами . На векторе  рассмотрим точку М₁ :

, т.е. М М₁ =       

Рассмотрим предел при :

 - производная функции  по направлению .

Пример:

  

Определение: Частные производные есть частный случай производной по направлению, если в качестве вектора , брать единичные векторы .

Определение: Градиентом функции u , называется вектор  

Пример:

            u - ?

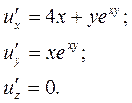
u =         

 

Определение: Производная  по направлению некоторого вектора  равна равна проекции вектора  на вектор .

Свойства градиента:

1)  Производная в данной точке по направлению вектора , имеет наибольшее значение, если направление вектора  совпадает с направление вектора градиента, и это наибольшее значение равно модулю градиента.

2)  Производная по направлению вектора перпендикулярному вектору градиента равна нулю.

3)  Если , то в точке М перпендикулярен к линии уровня , лежащей в плоскости xOy и проходящей через точку М.

Экстремум функции нескольких переменных.

Определение: Функция  имеет в точке М₀ (х₀,у₀) максимум, если больше, чем  для всех точек достаточно близких к ней, но отличных от нее.

Функция  имеет минимум в точке М₀ (х₀,у₀), если меньше, чем  для всех точек достаточно близких к ней, но отличных от нее.

Точки в которых частная производная функции нескольких переменных равна нулю или не существует, называются стационарными точками.

Теорема (необходимое условие экстремума): Если  достигает экстремума в точке с координатами (х₀,у₀), то каждая частная производная первого порядка от функции z, обращается в этой точке в нуль или не существует.

Доказательство:

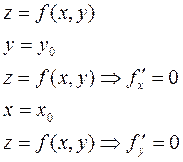
Теорема (достаточное условие экстремума): Пусть в некоторой области D содержащей точку М₀ (х₀,у₀), функция  имеет непрерывные частные производные до третьего порядка включительно и точка М₀ является стационарной точкой функции z. Тогда если:

1) 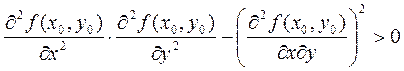  и , то в точке М₀ максимум.

2) 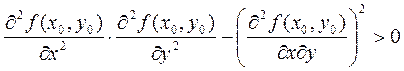и , то в точке М₀ минимум.

3) 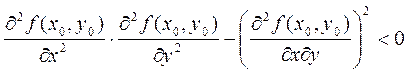, то нет экстремума.

4) 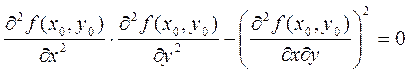, может быть, а может и не быть.

Пример:

1)

2)

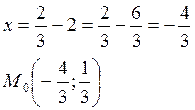
3)  в точке М₀ минимум.

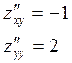
4) есть экстремум.

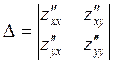
Условные экстремумы

Найти экстремум функции  при условии, что х и у связаны между собой соотношением .

Составляем функцию

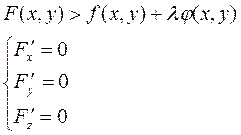
Пример:

Найти экстремум функции , при условии .

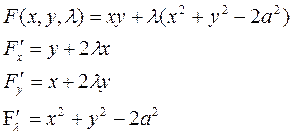
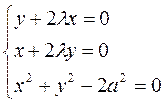
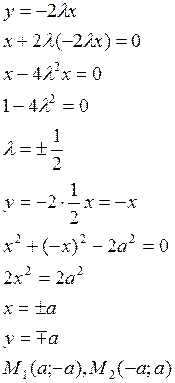
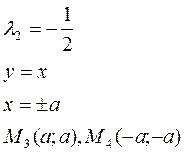
Элементы высшей алгебры.

Комплексные числа.

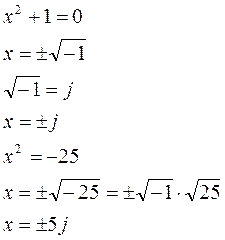
Комплексным числом z называется упорядоченная пара действительных чисел (a,b).

Число а, называется действительной частью числа z.

Число b, называется мнимой частью числа z.

Пример:

Числа вида jb называют, чисто мнимыми числами и они считаются корнями уравнения .

Геометрический смысл: комплексные числа отождествляются с точками плоскости хОу или с радиус-векторами этой плоскости.

Плоскость хОу называется комплексной плоскостью и обозначается С.

Два комплексных числа  и  считаются равными, если

Числа вида  называют действительными числами и изображаются точками действительной оси (Ох).

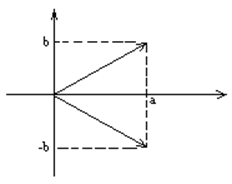Два комплексных числа у которых действительные части равны, а мнимые отличны только знаком называются взаимномопряженными.

То есть операция сопряжения отображает комплексное число относительно действительной оси.

 

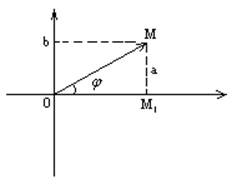
- модуль комплексного числа z.

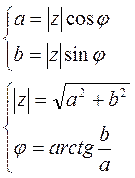
Замечание: аргумент комплексного числа многозначен и определяется с точностью до значения кратностью 2π.

- алгебраическая форма записи

- тригонометрическая форма записи

 - показательная форма записи

 - формула Эйлера

 - формула Эйлера для косинуса.

 - формула Эйлера для синуса.

 - периодическая с периодом 2π.

        

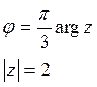
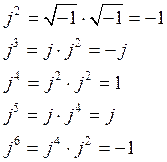
Действия над комплексными числами

1)

2)

3)  

4)

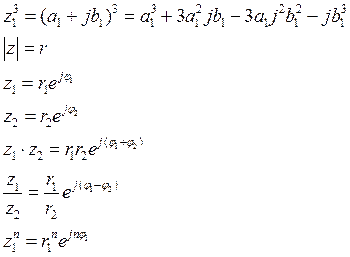
Формулы Муавра.

Определение: Корнем  из числа , называется всякое комплексное число w , такое что .

         

, возведем w в n-ную степень

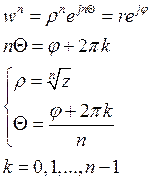
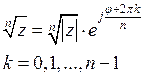
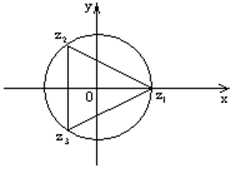
Т.е. корней n-ной степени из числа z ровно n штук и все они находятся на окружности радиуса  в вершинах правильного n-угольника.

Пример:

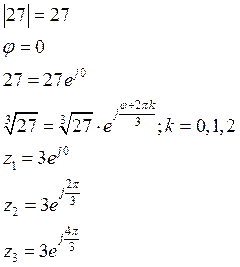
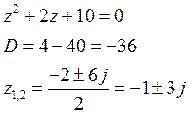
Разложение многочлена на множители.

Дробь не правильная, если степень числителя больше или равна степени знаменателя.

Деление будет на цело тогда и только тогда, когда  корень.