Ламинарный пограничный слой. Методы расчета ламинарного пограничного слоя

	Q

 

  Г л а в а   2

ЛАМИНАРНЫЙ ПОГРАНИЧНЫЙ СЛОЙ

2.1.  Методы расчета ламинарного

        пограничного слоя

	У

 

прощающие  допущения,  положенные в основу вывода уравнений пограничного слоя, привели к тому, что стало возможным принимать давление поперек пограничного слоя постоянным: ,а давление вдоль стенки считать совпадающим с давлением внешнего течения и поэтому рассматривать его как заданную функцию. Эти обстоятельства сделали ненужным уравнение движения в направлении, перпендикулярном к стенке.

Хотя уравнения пограничного слоя значительно проще уравнений Навье – Стокса, все же в математическом отношении они остаются значительно трудными. Точные аналитические решения (с получением расчетных формул) выполнены лишь для сравнительно узкого класса задач, например для струи, см. [1].

Для решения более общих задач применяют численные методы. Если процесс вычисления становится очень трудоемким, имеет смысл попробовать решить задачу приближенными методами, например интегральными. Ниже мы рассмотрим некоторые из этих методов в приложении к задачам ламинарного пограничного слоя.

Автомодельные решения уравнений пограничного слоя. Упрощающие допущения, сделанные при выводе уравнений пограничного слоя, выполняются тем лучше, чем больше число Рейнольдса. Поэтому выясним, каким образом развитие пограничного слоя на заданном теле зависит от числа Рейнольдса. Уравнения движения пограничного слоя в безразмерном виде:

;                        (2.1)

.                                         (2.2)

При этом граничными условиями будут:

U' = V' = 0при   у' = 0;  при у = ¥.

Из уравнений (2.1) и (2.2) видим, что при заданной форме тела, а следовательно, при заданном потенциальном течении развитие пограничного слоя зависит от числа Rе.

Путем дальнейшего преобразования уравнений (2.1) и (2.2) можно привести их к такому виду, который не содержит числа Рейнольдса. В самом деле, положив

,

, получим вместо уравнений (2.1) и (2.2) следующие:

;                          (2.3)

;                                          ( 2.4)

U' = V'' = 0при   у'' = 0;

 при у'' = ¥.

В уравнениях (2.3) и (2.4) число Rе отсутствует. Это означает, что решения системы уравнений (2.3) и (2.4) в координатах U'(х', у") и V''(х', у") также не зависят от числа Rе. Изменение числа Рейнольдса ведет за собой только аффинное преобразование пограничного слоя, изменяющее поперечную координату и скорость в поперечном направлении в  раз. Иными словами, для заданного тела безразмерные составляющие скорости

 и                                        (2.5)

являются функциями безразмерных координат

      и      , так как

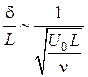                            ,                                           (2.6)

и эти функции в такой системе координат не зависят от числа Рейнольдса, или, как говорят, автомодельны по отношению к числу Рейнольдса (рис. 2.1).

а

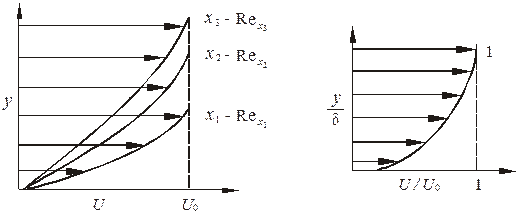
                                  б                                                                            в

Рис. 2.1. Пограничный слой на плоской стенке: а – схема течения;

б – профили скорости в сечениях х₁, х₂, х₃; в – профиль скорости

в безразмерных координатах

Под автомодельными решениями уравнений пограничного слоя (в иностранной литературе часто используется термин «подобные решения») будем понимать такие, для которых продольная составляющая скорости обладает следующим свойством: профили скоростей U(х, у) в двух различных поперечных сечениях х отличаются один от другого только масштабом координат Uи у (см. рис. 2.1).

Следовательно, для автомодельных решений профили скоростей во всех сечениях х, перпендикулярных стенке, можно привести к совпадению, если построить их в безразмерном виде, разделив для этого координаты Uи у на соответствующие масштабы. Будем называть такие профили скоростей аффинно подобными профилями.

Приведенная схема развития пограничного слоя на пластине дает наглядное представление об этом. За масштаб скорости удобно принять скорость на внешней границе пограничного слоя U₀, тогда безразмерная скорость U/U₀ в каждом сечении будет изменяться от нуля до единицы. Масштабом для расстояния у в соответствии с соотношением (2.6) может служить некоторая величина, пропорциональная толщине пограничного слоя в рассматриваемом течении.

Вопрос об автомодельных решениях важен прежде всего с математической точки зрения. Если имеются подобные решения, то, как мы ниже увидим, дифференциальные уравнения пограничного слоя, представляющие собой систему уравнений в частных производных, могут быть сведены к одному обыкновенному дифференциальному уравнению, что в математическом отношении означает существенное упрощение.

Одним из примеров автомодельного в указанном смысле решения уравнений пограничного слоя является решение Блазиуса для плоской пластины.

2.2.   Пограничный слой на плоской пластине.

         Решение Блазиуса

Простейшим применением уравнений пограничного слоя является течение вдоль плоской пластины. Такое течение было исследовано Блазиусом, что явилось первой иллюстрацией применения уравнений Прандтля.

Так как в рассматриваемом случае скорость потенциального течения постоянна, U₀ = const, то согласно уравнению Бернулли . Тогда уравнения движения и неразрывности пограничного слоя принимают вид

;                                  (2.7)

,                                         (2.8)

причем граничными условиями будут

U = V = 0при   у = 0;  при у = ¥.

В поставленной задаче обтекания бесконечной пластины нет характерной длины, поэтому можно предположить, что при определенным образом подобранных масштабах профили продольной скорости подобны между собой на различных расстояниях от передней кромки пластины.