Горячая штамповка выдавливанием осесимметричной детали, страница 11

Метод баланса работ основан на законе сохранения энергии, согласно которому работа внешних сил на соответствующих перемещениях равна работе внутренних сил деформирования. При этом упругая деформация не учитывается, материал заготовки считается несжимаемым, а работа внутренних сил определяется через интенсивности деформаций сдвига и касательных напряжений. Данный метод может быть использован для определения деформирующих усилий при процессах осадки, ковки и объёмной горячей штамповки. Он не позволяет находить распределение полей напряжений и деформаций [8].                                                                                                              

3 РЕШЕНИЕ ПОСТАВЛЕННЫХ ЗАДАЧ И ОБРАБОТКА РЕЗУЛЬТАТОВ

В нашем случае рассматриваем матрицу, состоящую из выходного цилиндрического участка 1 (калибрующего), заходного конического участка 2 (где происходит основная деформация) и цилиндрического контейнера – приёмника 3.

При установившемся сечении в выходном участке радиальное напряжение σ_ρ не может превышать предела текучести σ_S:

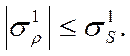                                                    (30)

В неравенстве (30) и далее верхний индекс соответствует номеру участка матрицы. Сопротивление движению металла будет создавать контактное трение.

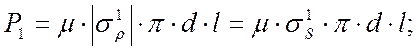           (31)

Удельное усилие на первом участке:

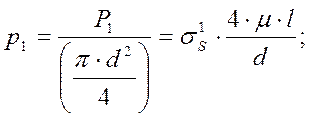                           (32)

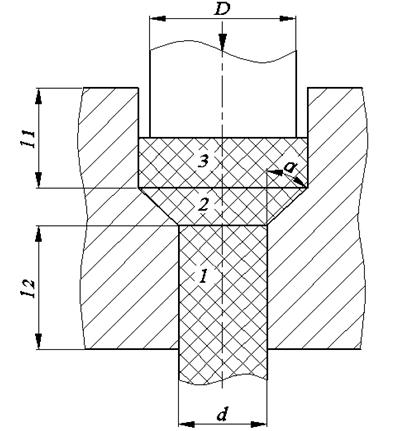
Рис. 9. Схема прессования.

Для горячего выдавливания стали исходя из характера нагрева и очистки заготовки, а также применяемой смазки принимаем следующее значение относительного контактного трения μ = 0,3. Величина предела текучести деформируемого металла σ_S зависит от температурно – скоростных условий процесса деформации и может быть определена по формуле

                       

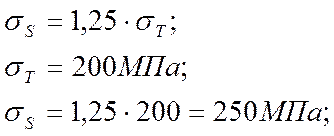
Подставляя данные значения в формулы (31) и (32) получаем

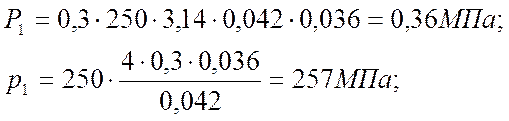
  Конический участок будем исследовать в сферической системе координат ρ, φ и θ. Верхняя и нижняя границы очага деформации могут быть представлены поверхностями шаровых секторов с радиусами b и a соответственно. Угол φ изменяется в пределах угла α, о от угла θ в окружном направлении ничего не зависит вследствие осевой симметрии задачи.

Давление на нижнюю границу с начала деформации равно Р₁, а давление на верхней границе  Р₂ является искомым. Пусть смещение частиц происходит только вдоль радиусов, следовательно, U_φ = U_θ = 0. Применяя метод баланса работ можно написать:

                                      (34)

где А₂ – работа силы Р₂;

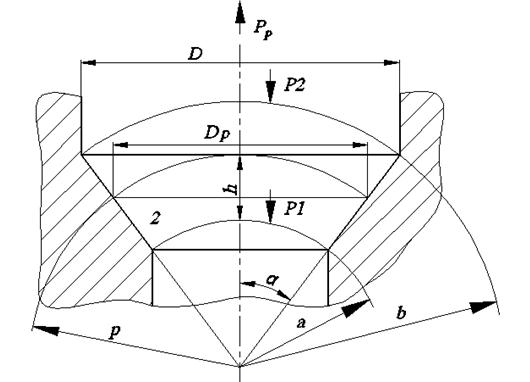
Рис. 10. Конический участок матрицы.

      А_Д – работа изменения формы;

      А_Т – работа сил трения;

      А₁ – работа силы Р₁.

Работа А₂ определяется формулой

                                                     (35)

где U_P – перемещение вдоль радиуса – вектора ρ.

Предварительно найдём деформации. Вследствие равенства кривизны в направлениях φ и θ, имеет место соотношения:

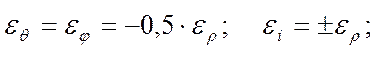                      (36)

А с учётом определения деформации:

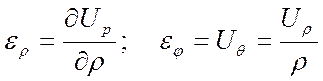;                            (37)

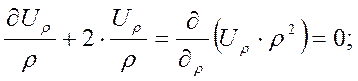                        (38)

интегрируя выражение (38) получим

                                                   (39)

с учётом граничных условий на верхней поверхности из выражения (39) получим

                                                   (40)

Предположим, что правая часть (39) слабо зависит от φ, так что вблизи верхней границы:

                                  

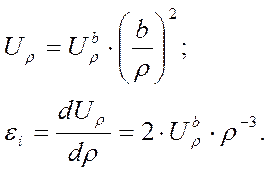
Работа деформации:

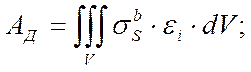                                     (43)

Элементарный объём в сферической системе координат для произвольного радиуса ρ даётся формулой

                                  (44)

Подставляя (42) и (44) в (43) получим:

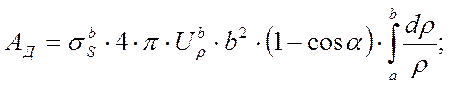
         (45)

Работа сил трения:

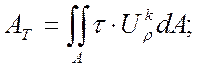                                            (46)

где τ, U_ρ^k – контактное напряжение и перемещение на контактной поверхности соответственно.

В силу (41):

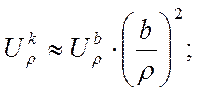                                             (47)

а дифференциал площади dA даётся соотношением:

                 (48)

подстановка (47) и (48) в (46) даёт:

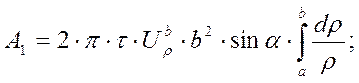                      (49)

Работа сопротивления со стороны участка 1 даётся формулой

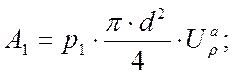                                        (50)

где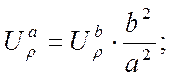   

Подставляя (35), (45) и (49) в (34), после интегрирования и элементарных преобразований получим:

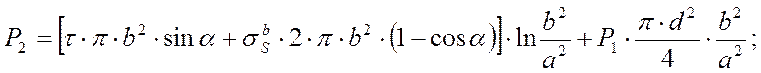                 (51)

С учётом соотношений:

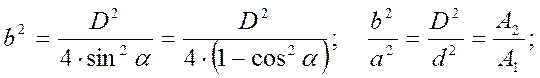                     (52)

где А₁, А₂ – площади сечения на входе и выходе матрицы.

Деление (51) на А₂ даёт удельное усилие на верхней границе:

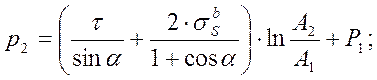                                            (53)

Касательное напряжение на предел текучести:

                                               (54)

Подставив значения переменных в формулы, получим:

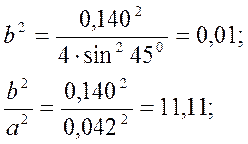
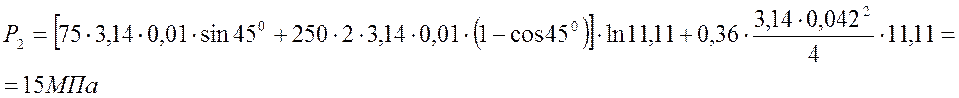
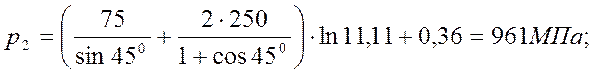
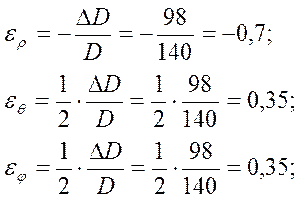
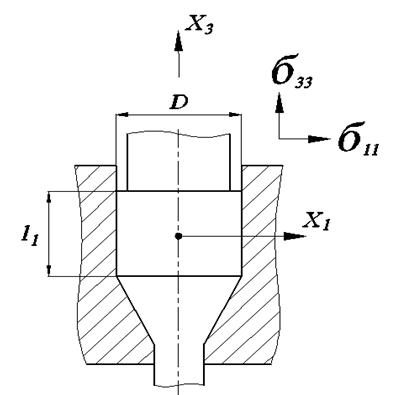
Рис. 11. Схема плоского напряжённого состояния

Для определения напряжений воспользуемся схемой плоской деформации.

                                      (55)

С учётом формулы (55) уравнения равновесия примут вид

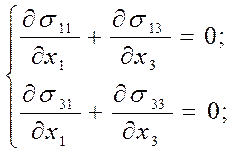                                              (56)

Продифференцируем данные уравнения по  (первое), по  (второе) и вычтем из первого второе.

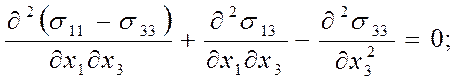               (57)

Запишем условие пластичности для плоского деформированного состояния:

;                                       (58)

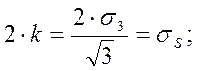                                                     (59)

Пусть напряжения не зависят от х₁:

                          

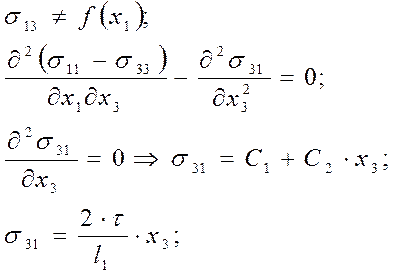
На нейтральном слое напряжение равняется нулю, откуда следует, что С₁ =0. На поверхности заготовки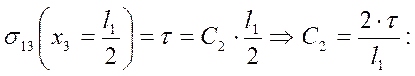

                                 

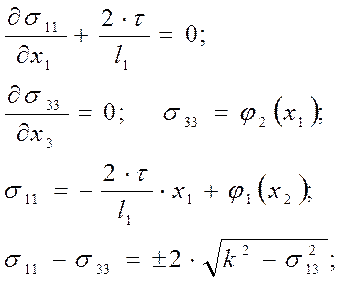
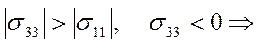 будет знак «+» 

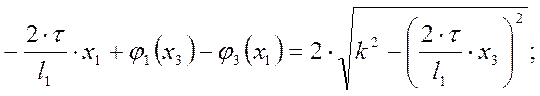                   (68)

Перенесём в (68) члены, содержащие х₁ в одну сторону, а члены, содержащие х₃, в другую, приравняв их некоторой константе С:

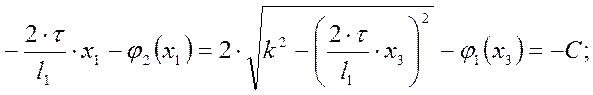            (69)

Приравнивание значений функций от разных переменных обусловлено тем, что значения этих функций совпадают лишь в случае, если их значения во всём диапазоне переменных являются константами. Из (69) определяются неизвестные функции, входящие в формулы (65) и (66):