бесконечно дифференцируема) в окрестности точки x0 и остаточный член Rn(x) стремится к нулю при n → ∞
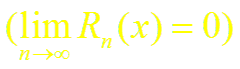
то из формулы Тейлора получается разложение функции f(x) по степеням (х – xo) называемое рядом Тейлора:
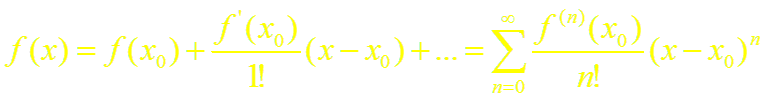
(2)
Если в ряде Тейлора положить xo = 0, то получим разложение функции по степеням х в так называемый ряд Маклорена:
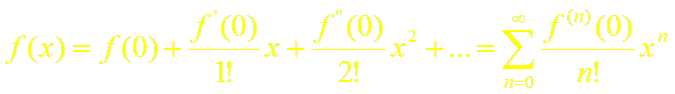
(3)
Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки xo. Но отсюда еще не следует, что он будет сходиться к данной функции f(x) он может оказаться расходящимся или сходиться, но не к функции f(x)
.
Так, например, функция
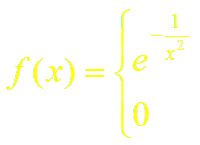
если х ≠ 0, если х = 0
имеет в точке х = 0 производные всех порядков, причем f (n) (0) = 0 при всяком п .Ряд Маклорена имеет вид:
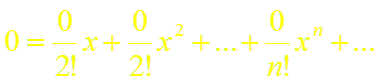
Он сходится, но его сумма S(x) в любой точке х равна нулю, а не f(x)
Пусть для функции f(x) составлен соответствующий ей ряд Тейлора.
Теорема 1
Для того чтобы ряд Тейлора (2) функции f(x) сходился к в точке х, необходимо и достаточно, чтобы в остаточный член формулы Тейлора (1) стремился к нулю при n → ∞, т.е. чтобы
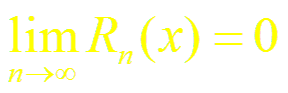
.
Пусть ряд Тейлора (2) сходиться к функции f(x) в некоторой окрестности точки xo, т.е.
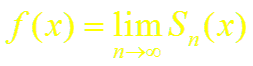
Так как n-я частичная сумма Sn(x) ряда (2) совпадает с многочленом Тейлора Pn(x), т.е. Sn(x) = Pn(x), находим:
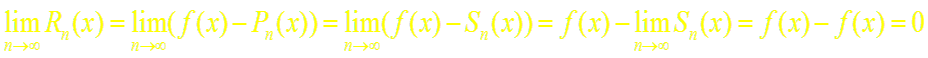
Обратно, пусть
Тогда
![]()
![]()
Замечание. Если ряд Тейлора (2) сходится к порождающей функции f(x) то остаточный член формулы Тейлора равен остатку ряда Тейлора, т.е. Rn(x) = rn(x). (Напомним, что Rn(x) = f(x) – Sn(x), a rn(x) = S(x) – Sn(x), где S(x) – сумма ряда Тейлора.)
Таким образом, задача разложения функции f(x) в степенной ряд сведена по существу к определению значений х, при которых Rn(x) → 0 (при n → ∞). Если сделать это не просто, то следует каким-нибудь иным способом убедиться, что написанный ряд Тейлора сходится к данной функции. На практике часто пользуются следующей теоремой, которая дает простое достаточное условие разложимости функции в ряд Тейлора.
Теорема 2
Если модули всех производных функций f(x) ограничены в окрестности точки x0 одним и тем же числом М > 0, то для любого х из этой окрестности ряд Тейлора функции f(x) сходится к функции f(x) т.е. имеет место разложение (2).
Согласно теореме (1), достаточно показать, что
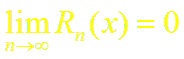
По условию теоремы (2) для любого n имеет место неравенство | f (n) (x)| ≤ M. Тогда имеем:
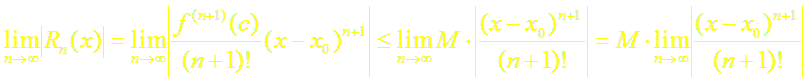
Осталось показать, что
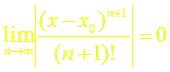
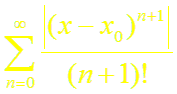
Для этого рассмотрим ряд
Так как
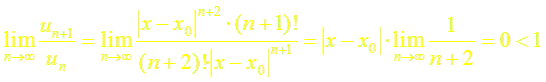
то по признаку Даламбера этот ряд сходится на всей числовой оси. Но тогда, в силу необходимого признака сходимости,
.
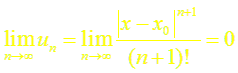
Следовательно,
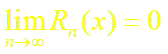
2.Разложение некоторых элементарных функций в ряд Тейлора (Маклорена)
Для разложения функции f(x) в ряд Маклорена (3) нужно:
а) найти производные f'(x), f"(x),... , f (n)(х),...;
б) вычислить значения производных в точке x0 = 0;
в) написать ряд (3) для заданной функции и найти его интервал сходимости;
найти интервал (– R; R), в котором остаточный член ряда Маклорена Rn(x) → 0 при n → ∞. Если такой интервал существует, то в нем функция f(x) и сумма ряда Маклорена совпадают.
г)
Замечание. В интервале сходимости степенного ряда остаточный член стремится к нулю при n → ∞. Приведем таблицу, содержащую разложения в ряд Маклорена некоторых элементарных функций (эти разложения следует запомнить):
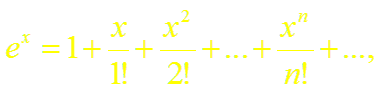
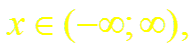
(4)
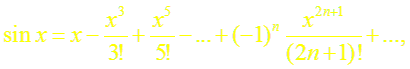
![]()
(5)
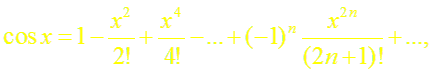
![]()
(6)
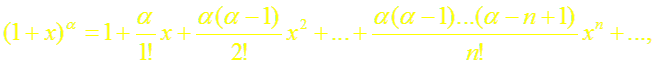
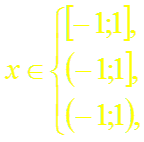
если α ≥ 0,
(7)
если – 1 < α < 0, если α ≤ – 1,
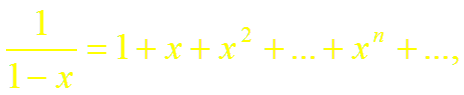
![]()
(8)
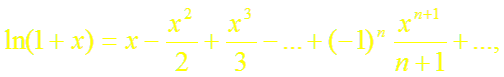
![]()
(9)
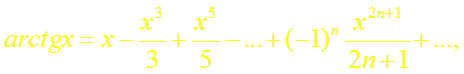
![]()
(10)
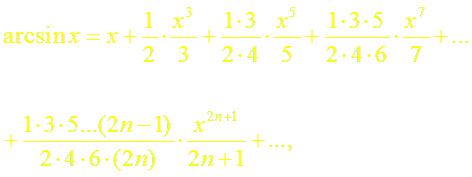
(11)
![]()
(12)
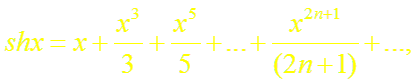
(13)
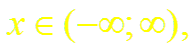
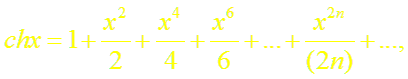
(14)
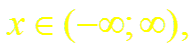
Докажем формулу (4). Пусть f(x) = ех.
Имеем:
а) f'(x) = ех, f"(x) = ех, . . . , f (n)(х) ех, . . .;
б) f (0)= 1, f'(0) = 1, . . ., f (n)(0) = 1, . . .;
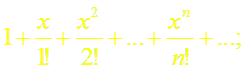
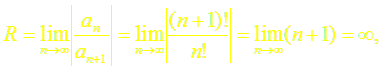
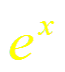
в)
~ т.е. ряд сходится в интервале (– ∞; ∞);
г) для всех
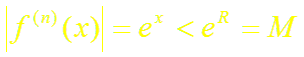
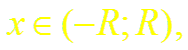
т.е. все производные в этом интервале ограничены одним и тем же числом М = eR. Следовательно, по теореме (2)
.
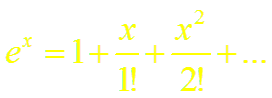
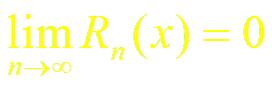
Таким образом,
Докажем формулу (5). Пусть f(x) = sin x.
Имеем:
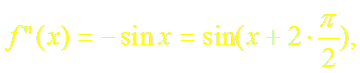
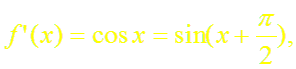
а)
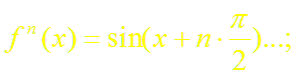
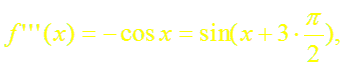
б)
n = 0, 2, 4, 6, . . .,
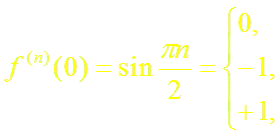
n = 3, 7, 11, . . .,
n = 1, 5, 9, . . .;
в)
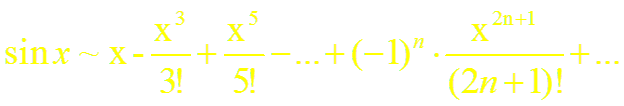
Легко проверить, что полученный ряд сходится на всей числовой оси, т.е. при всех
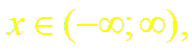
г) любая производная функции f(x) = sin x помодулю не превосходит единицы,
,
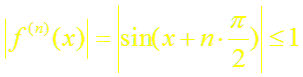
Следовательно, по теореме (2) имеет место разложение (5).
Докажем формулу (6). Пусть f(x) = cos x.
Формулу (6) можно доказать так же, как и формулу (5). Однако проще получить разложение функции cos x, воспользовавшись свойством 3 степенных рядов. Продифференцировав почленно ряд (5), получим:
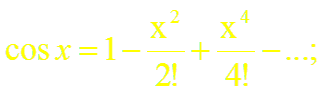
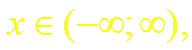
Докажем формулы (13), (14). Пусть f(x) = ch x (или f(x) = sh x). Заменив в формуле (18.4) х на – х, получим разложение функции е–х:
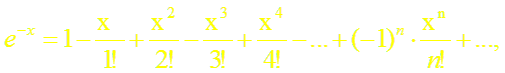
(15)
справедливое для всех
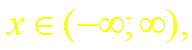
Суммируя (и вычитая) почленно равенства (4) и (15), получим разложение гиперболического косинуса (синуса):
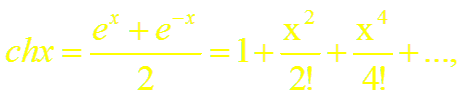
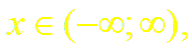
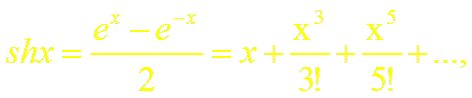
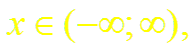
Формулы (13) и (14) доказаны.
Докажем формулу (7). Пусть f(x) = (1 +х)α, где α
R.
![]()
Имеем: а)
![]()
![]()
![]()
б)
. . . ,
![]()
![]()
![]()
![]()
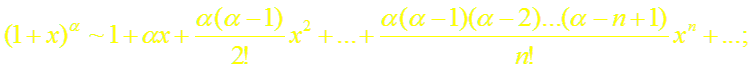
в) г)
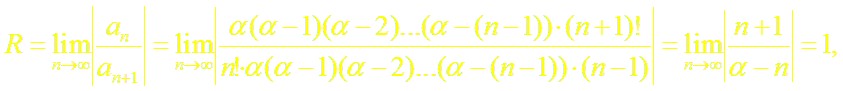
т.е. составленный для функции (1+ х)α ряд сходится в интервале
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.