Кинематическое исследование рычажного механизма качающегося конвейера графическим и аналитическим методами

соединяем точки Вi с точками Di, получим положения шатуна 4 ;

-  при построении планов механизма  отмечаем (с учетом геометрических соотношений) положения  центров масс звеньев 2 и 4 и строим  их  траектории;

-  проверяем с помощью линейки  и  транспортира  углы наклона  и длины звеньев, результаты измерений   заносим в таблицу 4;

-  определяем начальное D₁и конечное D₇ положение точки D;

-  одно из положений рабочего положения (в данном случае положение 3) рисуем основными линиями.

2.3 КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ МЕХАНИЗМА АНЛИТИЧЕСКИМ МЕТОДОМ

Сущность всех аналитических методов заключается в том, что линейные и угловые координаты, скорости и ускорения точек звеньев механизма определяются в виде аналитических  выражений. Исходными данными для вывода выражений является: структурная схема механизма, изображающая механизм в любом (расчетном) положении, исключая крайние; размеры звеньев; заданные положения обобщенных координат механизма; законы движения обобщенных координат механизма во времени. Если последнее не задано, то уравнения записываются в функции обобщенных координат, т.е. определяют не сами искомые функции, а их аналоги.

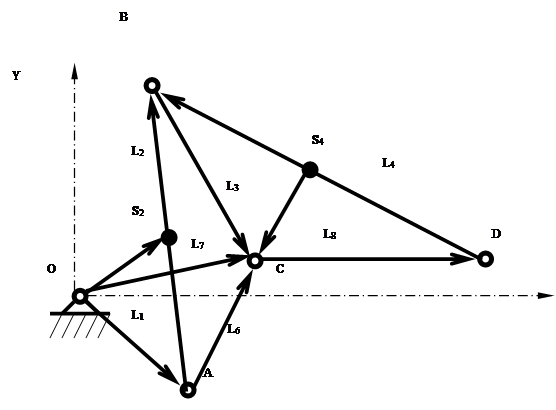
В данном курсовом проекте применим метод замкнутых векторных контуров для исследуемого механизма (рис. 0).

В соответствие с предложенным методом поступаем следующим образом.

1.  Рисуем в расчетном  (третьем) положении структурную схему исследуемого механизма.

2.  Структурную схему механизма располагаем в прямоугольной системе, начало которой помещаем в точку О.

3.  Со звеньями механизма, включая и стойку, связываем векторы произвольного направления так, чтобы их последовательность образовывала замкнутые контуры.

4.  Углы, определяющие положения векторов, отсчитываем от положительного направления оси ОХ против хода часовой стрелки.

			X

 

5.  Записываем уравнение замкнутости первого контура в векторной форме. Для этого обходим его периметр, например, в направлении вектора L₁, причем все векторы, совпадающие с направлением обхода, ставятся со знаком «+» и не совпадающие – со знаком «-». Так как мы ведем расчет для третьего положения механизма, то все линейные и угловые характеристики должны быть снабжены индексом «3». Но ввиду неудобства оформления здесь и далее этот индекс будем опускать, но подразумевать его.

6.  Рассмотрим контур OABCO:

L₁+L₂+L₃-L₇=0                        (3.1)

Уравнению (3.1) соответствуют два уравнения проекций на оси координат:

                                                                                                                                L₁*cosj₁+L₂*cosj₂+L₃*cosj₃-L₇*cosj₇=0 (3.2)

L₁*sinj₁+L₂*sinj₂+L₃*sinj₃-L₇*sinj₇=0

Среди величин, входящих  в уравнение  (3.2), переменными являются угол j₁,j₂,j₃. Угол j₁ является обобщенной координатой механизма, поэтому он должен быть задан.Из уравнений (3.2) подлежат определению углы j₂,j₃.

Анализ (3.2) показывает, что это уравнение сложно для решения.Для упрощения нахождения рассмотрим вместо контура OABCO контуры OACO и

ABCA. Для этого введем вектор L₆, соединяющий точки А и С. Получим:

L₁+L₆-L₇=0 (3.3)

L₂+L₃-L₆=0 (3.4)

Cпроецируем  (3.3) на оси координат:

 

L₁*cosj₁+L₆*cosj₆-L₇*cosj₇=0        

(3.5)

L₁*sinj₁+L₆*sinj₆-L₇*sinj₇=0

Из уравнения (3.5) находим угол наклона вектора L₆:

j₆= 

где: L₇соsф₇=X;           L₇sinф₇=Y;

и его модуль:

L₆=                      (3.7)   

Запишем уравнение (3.4) в развернутом виде и найдем углы j₂ и j₃ :

    L₂*cosj₂+L₃*cosj₃-L₆*cosj₆=0             

(3.8)

L₂*sinj₂+L₃*sinj₃-L₆*sinj₆=0

Слагаемые, содержащие угол j₃, переносим в правые части уравнения, возводим оба в квадрат и складываем. После преобразования получим:

L₃²=L₂²+2*LL(cos(-⁺(j₂-j₆))+L₆

j₂=b+j₆

b=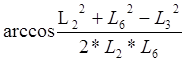

b-угол между векторами L₆ и L₇.

b=1.522рад

j₂=115.683⁰

Для определения угла j₃ используем любое из уравнений (3.8):

j₃=

j₃= p-25⁰=335⁰ (так как 4 четверть)   

Уравнения замкнутости 2-го контура BCDB:

L₃+L₈+L₄=0                                                                                          (3.11)

Cпроецируем  (3.11) на оси координат:

          L₃*cosj₃+L₈*cosj₈-L₄*cosj₄=0        

L₃*sinj₃+L₈*sinj₈-L₄*sinj₄=0

Учитывая, что j₈=0, получим:

          L₃*cosj₃+L₈ +L₄*cosj₄=0        

(3.12)    

L₃*sinj₃+L₄*sinj₄=0

j₄=                           (3.13)

j₄=

j₄=180⁰-12.2⁰=167,2⁰ (так как 3 четверть)

L₈=-L₃*cos j₃-L₄*cosj₄                                 (3.14)

L₈=-0,125*0,9+0,25*0,98=0,1325    

Для определения положений точек S₂ и  S₄запишем уравнения замкнутости контуров  OAS₂O  BCS₄B:

         L₁+L_as2 -L_s2o=0  (3.15)

L₃-L_cs4+L_s4b=0    (3.16)

Из этих уравнений находим координаты центров масс звеньев 2 и 4 :

 

S_2x=L₁*cosj₁+L_as2*cosj₂

(3.17)

S_2y= L₁*sinj₁+L_as2*sinj₂

 

S_2x=0,14*cos331.47+0,14*cos115,683=0,062

S_2y= 0,14*sin331.47+0,14*sin115,683=0,059

S_4x=L₃*cosj₃+L_bs4*cosj₄

(3.18)

S_4y= L₃*sinj₃+L_bs2*sinj₄

  

S_4x=0,35*cos155.438+0,35*cos168 =-0.341 м            (3.17)

S_4y= 0,35*sin155.438+0,35*sin168=0.258м

	j1	j2	j3	L8	j4
Графически
Аналитически	331.47	115.683	155.438	0,686	167,999
D,%

Т.к. аналоги  скоростей и ускорений не зависят от закона изменения j_1, то w₁=1 рад/c.

Продифференцируем по j₁ уравнение (3.2), получим:

                 L₁*sinj₁ -L₂*j₂’*sinj₂-L₃*j₃’sinj₃=0

(3.19)                                 

-L₁*cosj₁+L₂*j₂’cosj₂+L₃*j₃’cosj₃=0

Примем  j₁’=-1, так как угловая скорость звена 1 направлена по часовой стрелке. j₂ ‘_, j₃’-аналоги угловых скоростей звеньев 2 и 3.

Продифференцируем (3.12):

- L₃*j₃’*sinj₃ -L₂*j₂’*sinj₂-L₃*j₃’sinj₃=0

(3.20)                                 

-L₁*cosj₁+L₂*j₂’cosj₂+L₃*j₃’cosj₃=0

Решая (3.19) находим соответственно j₂’ и j₃’:

j₂’=

j₃’=

Из уравнений (3.20) соответственно находим L₈’:

Аналоги скоростей центров масс звеньев 2 и 3 получаем в проекциях на оси координат, дифференцируя по обобщенной координате (3.17) и (3.18):

 

S_2x’=

(3.25)

S_2y’=

    S_4x’=

(3.26)

S_4y’=

 

S_2x’=0,14×sin(331.47)-0,14*(-0.054)*sin(115.683)=-0,06

S_2y’=0,14×cos(331.47)+0,14×(-0.054)*cos(115.683)=-0,12

 

S_4x’=0,35*0.366×sin(155.438)-0,35*0,17*sin(168)=-0,041

S_4y’=0,35*0,366×cos(155.438)+0,35×0,17*cos168)=-0,058

Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений (3.19) и (3.20):

 

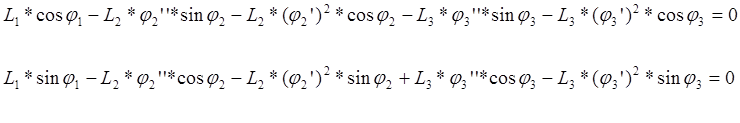
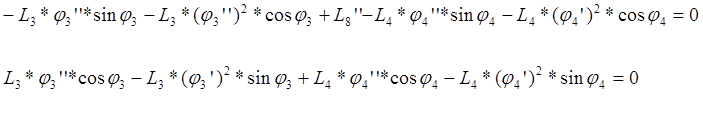
В этих уравнениях  j₂’’ _,j₃’’-аналоги угловых ускорений звеньев 2 и 3.

Для определения  j₂’’ _,j₃’’ решаем систему (3.27) обычным методом или вычитаем в первом уравнении системы угол  j₃ из аргументов всех тригонометрических функций:

      (3.29)

Из второго уравнения определяем

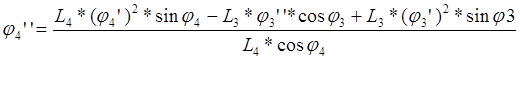                (3.31)

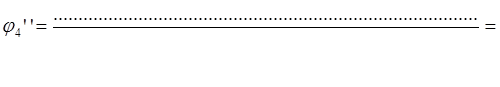
Из уравнений (3.20) находим L₈’’:

               (3.32)

Дифференцируя по обобщенной координате уравнения (3.25) и (3.26), определяем аналоги ускорений центров масс звеньев 2 и 3 в прекциях