![]()
![]()
![]()
![]()
![]()
![]() 22)
Сущность и применение метода симметричных составляющих для расчёта динамических
трёхфазных цепей с местной несимметрией. Применяется
для расчёта симметричных установившихся аврийных режимов в динамических
трёхфазных цепях, которые содержат обмотки генераторов и двигателей.
Динамические трёхфазные цепи могут также содержать ЛЭП и обмотки трансформаторов.
В динамических трёхфазных цепях имеется взаимная индуктивность между фазами.
Сущность метода симметричных составляющих заключается в разложении
несимметричной системы векторов а, b, с, на
симметричные составляющие прямой обратной и нулевой последовательности: А=Аеjα=A1+A2+A0, B=Bеjβ=B1+B2+B0, C=Cеjγ=C1+C2+C0. 1)
Составляющие прямой последовательности. A1=А1ejα1; B1=a2A1, C1=aA1; 2)Составляющие
обратной последовательности: A2=А2ejα2; B2=aA2; С2=a2A2;
3)Составляющие нулевой последовательности: А0=В0=С0=
А0ejα0. Расчёт
составляющих фазы А: A1=(А+аВ+а2С)/3;
A2=(А+а2В+аС)/3;
A0=(А+В+С)/3.
В двигателях и генераторах составляющие токов прямой последовательности создают
круговое вращающееся по направлению вращению ротора магнитное поле, а
составляющие обратной последовательности создают вращающееся навстречу ротору
магнитное поле, составляющие нулевой последовательности создают неподвижное
пульсирующее магнитное поле. Цепи с местной несиметрией в нормальном режиме
симметричны, а в аварийном имеют местную несимметрию ( к.з. или обрыв фазы).
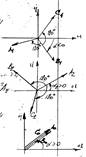
Пусть задана ЭДС генератора и все сопротивления элемента схемы. Требуется найти
токи и напряжения. Заменим несимметричный участок схемы тремя источниками ЭДС с
неизвестными напряжениями UA’A”; UB’B”; UC’C”. Разложим неизвестные напряжния на
симметричные составляющие U1, U2, U0, приняв
фазу А за главную. Составляющие схемы «1», «2», «0», последовательностей. Из
этих схем по 2-му закону Кирхгофа: 1)(ZГ1+ZЛ1+Z1’)I1+U1=E1; 2) (ZГ2+ZЛ2+Z2’)I2+U2=0; 3) (3ZN+ZГ0+Z0’)I0+U0=0. Некоторые виды несимметричных участков
цепи: UB=0;
IA=0; IC=0- однофазное к.з. на землю
фазы B; UA=0; UB=0; IC=0- обрыв фазы C; IA=0, UВ=UC, -IC=IB- замыкание C и В. В
этих дополнительных уравнениях нужно напряжения и токи выразить через их
симметричные составляющие. Решив совместно основные дополнительные уравнения,
найдём симметричные составляющие токов, а затем определим и все остальные
искомые величины.
22)
Сущность и применение метода симметричных составляющих для расчёта динамических
трёхфазных цепей с местной несимметрией. Применяется
для расчёта симметричных установившихся аврийных режимов в динамических
трёхфазных цепях, которые содержат обмотки генераторов и двигателей.
Динамические трёхфазные цепи могут также содержать ЛЭП и обмотки трансформаторов.
В динамических трёхфазных цепях имеется взаимная индуктивность между фазами.
Сущность метода симметричных составляющих заключается в разложении
несимметричной системы векторов а, b, с, на
симметричные составляющие прямой обратной и нулевой последовательности: А=Аеjα=A1+A2+A0, B=Bеjβ=B1+B2+B0, C=Cеjγ=C1+C2+C0. 1)
Составляющие прямой последовательности. A1=А1ejα1; B1=a2A1, C1=aA1; 2)Составляющие
обратной последовательности: A2=А2ejα2; B2=aA2; С2=a2A2;
3)Составляющие нулевой последовательности: А0=В0=С0=
А0ejα0. Расчёт
составляющих фазы А: A1=(А+аВ+а2С)/3;
A2=(А+а2В+аС)/3;
A0=(А+В+С)/3.
В двигателях и генераторах составляющие токов прямой последовательности создают
круговое вращающееся по направлению вращению ротора магнитное поле, а
составляющие обратной последовательности создают вращающееся навстречу ротору
магнитное поле, составляющие нулевой последовательности создают неподвижное
пульсирующее магнитное поле. Цепи с местной несиметрией в нормальном режиме
симметричны, а в аварийном имеют местную несимметрию ( к.з. или обрыв фазы).
Пусть задана ЭДС генератора и все сопротивления элемента схемы. Требуется найти
токи и напряжения. Заменим несимметричный участок схемы тремя источниками ЭДС с
неизвестными напряжениями UA’A”; UB’B”; UC’C”. Разложим неизвестные напряжния на
симметричные составляющие U1, U2, U0, приняв
фазу А за главную. Составляющие схемы «1», «2», «0», последовательностей. Из
этих схем по 2-му закону Кирхгофа: 1)(ZГ1+ZЛ1+Z1’)I1+U1=E1; 2) (ZГ2+ZЛ2+Z2’)I2+U2=0; 3) (3ZN+ZГ0+Z0’)I0+U0=0. Некоторые виды несимметричных участков
цепи: UB=0;
IA=0; IC=0- однофазное к.з. на землю
фазы B; UA=0; UB=0; IC=0- обрыв фазы C; IA=0, UВ=UC, -IC=IB- замыкание C и В. В
этих дополнительных уравнениях нужно напряжения и токи выразить через их
симметричные составляющие. Решив совместно основные дополнительные уравнения,
найдём симметричные составляющие токов, а затем определим и все остальные
искомые величины.
![]()
![]()
![]() 23)Оссобености
существования в трёхфазных цепях составляющих напряжений и токов нулевой
последовательности. 1)Линейное напряжение UAB, UBC, UCA – не содержат нулевой последовательности, так как они
образуют треугольник и их сумма равна нулю. Фазные токи пропорциональны
линейным напряжениям, поэтому они также не содержат нулевой последовательности.
UAB0=0, UBC0=0, UCA0=0, IAB0=UAB0/Z0=0, IBC0=UBC0/Z0=0, ICA0=UCA0/Z0=0. Ток
нулевого провода IN содержит
составляющие только нулевой последовательности, т.к. IА0= IВ0=IC0=(IA+IB+IC)/3, то IЛ= IA+IB+IC=3IA0, то линейные токи и фазные напряжения
содержат нулевую последовательность, если есть связь с нулевым проводом или с
землёй.
23)Оссобености
существования в трёхфазных цепях составляющих напряжений и токов нулевой
последовательности. 1)Линейное напряжение UAB, UBC, UCA – не содержат нулевой последовательности, так как они
образуют треугольник и их сумма равна нулю. Фазные токи пропорциональны
линейным напряжениям, поэтому они также не содержат нулевой последовательности.
UAB0=0, UBC0=0, UCA0=0, IAB0=UAB0/Z0=0, IBC0=UBC0/Z0=0, ICA0=UCA0/Z0=0. Ток
нулевого провода IN содержит
составляющие только нулевой последовательности, т.к. IА0= IВ0=IC0=(IA+IB+IC)/3, то IЛ= IA+IB+IC=3IA0, то линейные токи и фазные напряжения
содержат нулевую последовательность, если есть связь с нулевым проводом или с
землёй.

 24)Представление
периодических негармонических (несинусоидальных) напряжений и токов в
тригонометрический ряд Фурье. Действующие значения периодических напряжений и
токов. Периодические несинусоидальные токи и напряжения- это
такие величины, которые изменяются во времени по периодическому
несинусоидальному закону. Несинусоидальный сигнал раскладывается в ряд Фурье,
т.е. представляется суммой гармоник, а решение ведётся для каждой из гармоник.
Периодическую функцию можно разложить в ряд Фурье, если выполняются условия:
1)На любом конечном интервале функция должна содержать конечное число разрывов i-го рода (т.е. предел функции с права и с лева должен
быть конечен). 2)На любом конечном интервале функция должна иметь конечное
число максимумов. f(wt)=A0+A1Msin(wt+φ1)+A2Msin(2wt+φ2)=A0+∑AKMsin(Kwt+φK), где A0-
постоянная составляющая, A1Msin(wt+φ1)- первая гармоника, φ1-фаза
первой гармоники. Остальные синусоиды- высшие гармоники
24)Представление
периодических негармонических (несинусоидальных) напряжений и токов в
тригонометрический ряд Фурье. Действующие значения периодических напряжений и
токов. Периодические несинусоидальные токи и напряжения- это
такие величины, которые изменяются во времени по периодическому
несинусоидальному закону. Несинусоидальный сигнал раскладывается в ряд Фурье,
т.е. представляется суммой гармоник, а решение ведётся для каждой из гармоник.
Периодическую функцию можно разложить в ряд Фурье, если выполняются условия:
1)На любом конечном интервале функция должна содержать конечное число разрывов i-го рода (т.е. предел функции с права и с лева должен
быть конечен). 2)На любом конечном интервале функция должна иметь конечное
число максимумов. f(wt)=A0+A1Msin(wt+φ1)+A2Msin(2wt+φ2)=A0+∑AKMsin(Kwt+φK), где A0-
постоянная составляющая, A1Msin(wt+φ1)- первая гармоника, φ1-фаза
первой гармоники. Остальные синусоиды- высшие гармоники
f(wt)= A0+ B1Msin(wt)+B2Msin(2wt)+…+C1Mcos(wt)+ C1Mcos(wt)+ C2Mcos(2wt)+…
A0=(1/T)∫f(wt)dt; BKM=(2/T)∫f(wt)sin(Kwt)dt; CKM=(2/T)∫f(wt)cos(Kwt)dt; Разложение в ряд А: AKM=(BKM2+CKM2)1/2 φK=arctg(CKM/BKM). Спектральное представление амлитуды:
Действующие значения: F=(1/T)(∫f2(wt)dt)1/2, F= [(A02/2)+ (A1M2/2)]1/2,
F= A1M/21/2-для синусоид.
![]() 25)Активная,
реактивная и полная мощности при периодических негармонических
(несинусоидальных) напряжениях и токах. U(t)=U0+U1sin(wt+α1)+U2sin(wt+α2)+…,
i(t)=I0+i1(t)+i2(t)… Активная
периодического тока произвольной формы определяется, как средняя мощность за период
Р=(1/T)(∫U(t)i(t)dt. Если
мнгновенные значения напряжения и тока выразить в виде тригонометрических
рядов, то получим: Р=(1/T)∫[∑Ukmsin(kwt+Ψuk)][∑Ikmsin(kwt+Ψik)]dt=(1/T)∫[∑UkmIkmsin(kwt+Ψuk)* *sin(kwt+Ψik)]dt=U0I0+∑(UkmIkmcosφk)/2=∑UkIkcosφk где φk=Ψuk-Ψik. Следовательно средняя мощность несинусоидального тока
равна сумме средних мощностей отдельных гармоник P=∑Pk – равенство Парсеваля. Понятие
полной мощности S, определяемой как произведение
действующих значений тока и напряжения S=UI=[∑U2k∑I2k]1/2. Понятие реактивной мощности,
определяемой как сумма реактивных мощностей отдельных гармоник: Q=∑UkIksinφk=∑Qk. Для несинусоидальных токов в отличие от синусоидальных,
квадрат полнлй мощности обычно больше суммы квадратов P и Q S2≥P2+Q2.
25)Активная,
реактивная и полная мощности при периодических негармонических
(несинусоидальных) напряжениях и токах. U(t)=U0+U1sin(wt+α1)+U2sin(wt+α2)+…,
i(t)=I0+i1(t)+i2(t)… Активная
периодического тока произвольной формы определяется, как средняя мощность за период
Р=(1/T)(∫U(t)i(t)dt. Если
мнгновенные значения напряжения и тока выразить в виде тригонометрических
рядов, то получим: Р=(1/T)∫[∑Ukmsin(kwt+Ψuk)][∑Ikmsin(kwt+Ψik)]dt=(1/T)∫[∑UkmIkmsin(kwt+Ψuk)* *sin(kwt+Ψik)]dt=U0I0+∑(UkmIkmcosφk)/2=∑UkIkcosφk где φk=Ψuk-Ψik. Следовательно средняя мощность несинусоидального тока
равна сумме средних мощностей отдельных гармоник P=∑Pk – равенство Парсеваля. Понятие
полной мощности S, определяемой как произведение
действующих значений тока и напряжения S=UI=[∑U2k∑I2k]1/2. Понятие реактивной мощности,
определяемой как сумма реактивных мощностей отдельных гармоник: Q=∑UkIksinφk=∑Qk. Для несинусоидальных токов в отличие от синусоидальных,
квадрат полнлй мощности обычно больше суммы квадратов P и Q S2≥P2+Q2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.