Математика \ Математический анализ

Числовые ряды. Сходимость и сумма ряда. Действия с рядами. Свойства абсолютно сходящихся рядов, страница 2

Следствие 1. Пусть в условиях теоремы 1 выполняется неравенство an£ сbn  при любом n,  где с - положительная постоянная. . Тогда

1)  если сходится  ряд (2), то сходится и ряд (1);

2)  если расходится ряд (1), то расходится и ряд (2).

Следствие 2. Пусть в условиях теоремы 1 существует конечный предел = L . Тогда

1)  если сходится  ряд (2), то сходится и ряд (1);

2)  если расходится ряд (1), то расходится и ряд (2).

Теорема 1. Пусть в условиях теоремы 1 для всех номеров n справедливо неравенство  . Тогда

1)  если сходится  ряд (2), то сходится и ряд (1);

2)  если расходится ряд (1), то расходится и ряд (2).

Доказательство. По условию теоремы справедливы неравенства . Перемножая эти неравенства почленно, после сокращения получаем и по теореме 2 получаем утверждение теоремы 3.

4.  Достаточные признаки сходимости знакопостоянного ряда Даламбера, Коши, интегральный признак.

Сравнивая ряды с рядом геометрической прогрессии получим следующие достаточные признаки сходимости рядов с положительными членами.

Теорема 1 (признак Даламбера). Пусть дан ряд с положительными членами. Если для всех номеров n или для всех номеров n, начиная с некоторого места, справедливо неравенство

1) , то ряд сходится; 2) , то ряд сходится.

Теорема 2 ( предельный признак Даламбера). Пусть дан ряд с положительными членами. Пусть существует предел  .    Тогда:

1)  , то ряд сходится; 2) , то ряд сходится.

Теорема 3 (признак Коши). Пусть дан ряд с положительными членами. Если для всех номеров n или для всех номеров n, начиная с некоторого места, справедливо неравенство

1) , то ряд сходится; 2) , то ряд сходится.

Теорема 4 ( предельный признак Коши). Пусть дан ряд с положительными членами. Пусть существует предел   .   Тогда:

2)  , то ряд сходится; 2) , то ряд сходится.

Теорема 5 (интегральный признак сходимости). Пусть дан ряд с положительными членами, и не взрастают начиная с некоторого места, т.е. для всех n ³ m имеем an ³ an+1. Пусть далее функция f(x) , определена при всех x ³ 1, непрерывная и невозрастающая при всех x ³ 1 и f(n) = an для любого n ³ 1. Тогда ряд (1) сходится тогда и только тогда, когда сходится несобственный интеграл

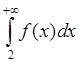.                                                                                                   (3)

Доказательство. По условию an = f(n) ³ f(x) ³ f(n+1) = an+1 для всех n ³ 1. Интегрируя это неравенство, получаем

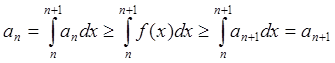. Рассмотрим три ряда

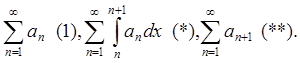
Если ряд (1) сходится, то сходится ряд (**) и по признаку сравнений сходится ряд (*), равный интегралу (3). Если ряд (1) расходится, то расходится ряд (*) и интеграл (3).

5. Знакочередующиеся ряды. Признак Лейбница. Ряд, все члены которого попеременно чередуются имея, то положительные, то отрицательные знаки, называется знакочередующимся рядом . Знакочередующийся ряд удобно записать в виде

.                                     (1)

сли все члены ряда больше нуля, то ряд называется рядом с положительными членами.

Теорема 5 (признак Лейбница). Пусть выполняются условия

1)  все члены ряда (1) образуют невозрастающую по модулю последовательность, т.е.;

Скачать файл