Отображения и их виды. Обратное отображение. Мощность множества. Счетные множества

220400                                                  Математический анализ                                        Толстиков А.В.

Курс 1. Семестр 1. Лекция 2. Отображения.

План

1.  Отображения.  2.  Виды отображений. 3. Обратное отображение. 4. Мощность множества. Счетные множества.

Литература: Ермаков В.И. с. 276-280. Ильин В.А., с.183-195. Шнейдер В.Е. 285-296. Кремер Н.Ш. 251-266.

1.  Отображения.

Определение 1.1. Бинарным отношением f между множествами X и Y  называется любое подмножество множества X´Y.

Определение 1.2. Бинарное отношение f между множествами X и Y  называется  отображением множества X в множество Y, если для любого элемента xÎX существует один и только один элемент yÎY такой, что (x, y)Îf .

Отображение f множества X в Y называется также функцией, определенной на множестве X со значениями в множестве Y.

Символически отображение f множества X в Y записывается в виде: f: X ® Y. То, что (x, y)Îf, записывается также в виде y = f(x)  или f: x a y.

При этом область определения D(f) бинарного отношения f совпадает с X и называется областью определения отображения или функции f, область значений E(f) называется множеством значений отображения или функции f. Если (x, y)Îf, то элемент y называется образом элемента x при отображении f  и обозначается символом      y = f(x), а элемент x - прообразом элемента y. Также при этом говорят, что элемент x есть аргумент или более точно, значение аргумента, а f(x) - значение функции в точке x. Множество X называется также областью отправления, Y - областью прибытия отображения f.

Иногда отображением f множества X в Y называется правило, которое каждому элементу xÎX ставит в соответствие единственный элемент yÎY , обозначаемый f(x).

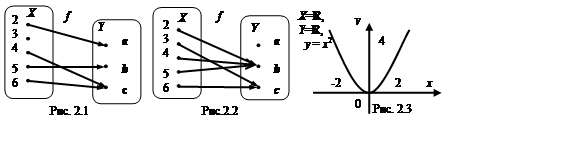Отображения задаются теми же способами, что и бинарные отношения. На рис. 1.10 и 1.7 представлены отображения, заданные стрелками и графически.

Стрелочное изображение отображения f: X ® Y имеет следующие особенности:

1)  из каждой "точки" множества X  выходит только одна стрелка;

2)  две стрелки не могут иметь общее начало.

Если X, YÍ R, то функция называется числовой функцией. Отметим, что множество G точек плоскости xOy является графиком некоторой числовой функции тогда и только тогда, когда каждая прямая параллельная оси Oy пересекает G не более чем в одной точке.

Определение 1.3. Образом множества   A Í X  при отображении f: X ®Y называется множество f (A) = {f(x)| xÎ A }.

Например, на рис. 1.11 f ({2, 4}) = {b}.

Отметим, что f (X) = E(f).

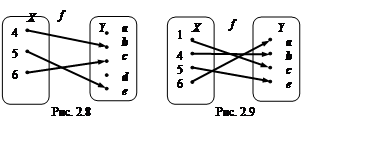
Определение 1.4. Прообразом или полным прообразом  множества BÍ X  при отображении f: X ®Y называется множество f ^-1(A) = {xÎ X | f(x)ÎB }.

Например, на рис. 2.2 f ^-1({b}) = {2, 4, 5}.

Определение 1.5. Два отображения f₁: X₁ ® Y₁, f₂: X₂ ® Y₂ называются равными, обозначается f₁ = f₂, если

1)  X₁= X₂,

2)  для любого xÎ X₁ имеем f₁(x) = f₂(x).

Определение 1.6. Композицией двух  отображений f: X®Y, g: Y®W называется отображение : X®W определяемое для любого xÎ X формулой:

Если f и g числовые функции, то называют также сложной функцией.

Приведенная на рис. 1.9 треугольная диаграмма наглядно иллюстрирует то, что при выполнении отображения  сначала выполняется отображение f , а затем - отображение g.

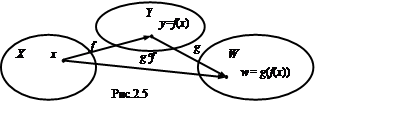Например, если f и g отображения R в R, определенные формулами f: xa x², g: xa x+1, то : x a x²+1, : x a (x+1)².

Теорема 1.1. Операция композиции обладает свойством ассоциативности, т.е.  для любых трех отображений  f: X®Y,   g: Y®W , h: W®Z.

Доказательство.  Так как для любого элемента xÎ X имеем

то по определению 1.4 утверждение теоремы справедливо.

Определение 1.7. Отображение e_X: X®X называется единичным или тождественным отображением, если e_X(x) =x для любого xÎ X.

Теорема 1.2. Для любого отображения  f: X®Y .

Доказательство. ТУ 1.2.

Определение 1.8. Отображение f: X₁®Y называется сужением или ограничением отображения g: X₂®Y на X₁, если

1)  X₁Í X₂,

2)  для любого xÎ X₁ имеем f(x) = g(x).

В этом случае пишут f= g½_A, а также говорят, что g продолжениеили расширение отображения f.

 2. Виды отображений. Обратное отображение.

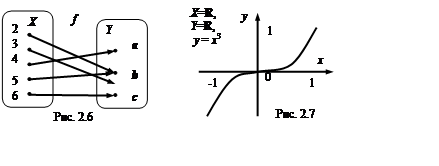
Определение 2.1. Отображение f  множества X  в  Y называется  отображением множества X  на  Y, или сюръективным, или сюръекцией, если для любого yÎ Y найдется такой элемент xÎ X, что f(x) =y.

Таким образом, f: X®Y сюръекция тогда и только тогда, когда E(f) = Y.

Например, отображение f: R®[0, +¥), f: xax², является сюръекцией, см. также рис. 1.5, 1.11   . Отметим, что отображения на рис 2.2, 1.7 не являются таковыми.

Определение 2.2. Отображение f  множества X  в  Y называется  взаимно однозначным отображением множества X  в  Y , или инъективным, или инъекцией, или вложением, если для любых  x₁,  x₂ Î X   из     x₁ ¹ x₂    следует, что f(x₁)  ¹ f(x₂).

Например, отображение f:R\{0}®R, f: xa1/x, является инъекцией