220400 Алгебра и геометрия Толстиков А.В.
Определение линейного оператора и его свойства. Матрица линейного оператора.
1. Связь между матрицами линейного оператора в различных базисах.
2. Операции над линейными операторами.
3. Характеристическое уравнение линейного оператора.
4. Собственные векторы и собственные значения линейного оператора, и их связь с корнями характеристического уравнения.
5. Линейные операторы с простым спектром.
Рекомендуемая литература
1. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1984.
2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. 1997.
3. Воеводин В.В. Линейная алгебра.. М.: Наука 1980.
4. Сборник задач по для втузов. Линейная алгебра и основы математического анализа. Под ред. Ефимова А.В., Демидовича Б.П.. М.: Наука, 1981.
5. Бутузов В.Ф., Крутицкая Н.Ч., Шишкин А.А. Линейная алгебра в вопросах и задачах. М.: Физматлит, 2001.
6. Воеводин В.В. Линейная алгебра. М.: Наука, 1980.
Линейные операторы
1. Определение линейного оператора и его свойства. Матрица линейного оператора. Пусть V - векторное пространство над полем P.
Определение 1. Линейным оператором A в векторном пространстве Vназывается отображение A векторного пространства V в V обладающее свойствам:
(1) (" a, b Î L) A(a + b) = Aa + Ab;
(2) (" a Î L) (" a Î R) A(aa) =a( Aa).
Свойство 1. Линейный оператор переводит нулевой вектор в нулевой вектор: A0 = 0.
Свойство 2. Линейный оператор переводит противоположный вектор в соответствующий противоположный вектор: A(-a) =- Aa.
Свойство 3. Линейный оператор переводит линейную комбинацию векторов в соответствующую линейную комбинацию образов этих векторов: A(a1a1 + a2a2 + …+akak ) = a1 Aa1 + a2 Aa2 + …+ak Aak.
Свойство 4. Линейный оператор переводит линейно-зависимую систему векторов в линейно-зависимую систему векторов.
Матрица линейного оператора. Пусть v =(v1, v2, …, vn) - базис векторного пространства V, A - линейный оператор в векторном пространстве V. Разложим образы Av1, Av2, …, Avk векторов базиса по векторам того же базиса:
Av1 = a11 u1 + a21 u2 + ... + am1 um , Av2 = a12 u1 + a22 u2 + ... + am2 um ,. . ., Avn = a1n u1 + a2n u2 + ... + amn um .
Определение 2. Матрицей линейного оператора A в данном базисе называется матрица
А
= 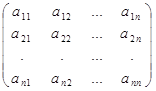 , столбцы которой есть координатные
строки образов базисных векторов векторного пространства V, выраженные через
тот же базис.
, столбцы которой есть координатные
строки образов базисных векторов векторного пространства V, выраженные через
тот же базис.
Лемма 1. Пусть v1, v2, ..., vn базис векторного пространства V, a1, a2, ..., an - произвольная система векторов из U. Тогда существует линейный оператор A векторного пространства V, при котором Av1 = a1, Av2 = a2, ..., Avn = an.
Теорема 1.Пусть V - векторное пространство над полем Р размерности n. При выбранном базисе существует взаимно-однозначное соответствие между множеством линейных операторов V множеством Мn(P) матриц порядка n с элементами из поля Р.
Пусть а = v(x1, x2, ..., xn) t . Тогда Aa = vAj (x1, x2, ..., xn) t . Отсюда получаем следующие формулы преобразования координат:
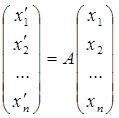 ,
,![]()
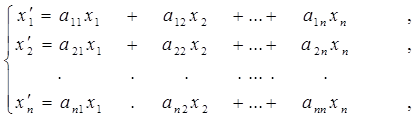
где Aa = v (x¢1, x¢2, ..., x¢n) координатный столбец вектора Aa в данном базисе.
2. Связь между матрицами линейного оператора в различных базисах.
Определение 1. Матрицы A и B называются подобными, если существует такая матрица T, что B = T -1 A T.
Теорема 1. Матрицы линейного оператора A векторного пространства V - подобны, т. е. если A и B матрицы линейного оператора j соответственно относительно базисов v = (v1, v2, ..., vn) и u = (u1, u2, ..., un) векторного пространства V, T- матрица перехода от первого базиса ко второму, то B = T -1 A T .
Лемма 1. Пусть v = (v1, v2, ..., vn) - базис векторного пространства V, A и С - матрицы размерности n´ m. Если vA = vС, то A = С.
Доказательство теоремы. Пусть T = (tij) - матрица перехода от первого базиса. По определению матрицы перехода от базиса v к базису u имеем u = vT . По определению матрицы линейного оператора имеем
A(u) = (Au1, Au2, ..., Aun) = (u1, u2, ..., un)B = uB = (vT)B =v(TB) . (1)
С другой стороны
A(u) == (Au1, Au2, ..., Aun)=(A(t11 v1 + t21 v2 + ...+ tn1 vn), A( t12 v1+ t22 v2 + ...+ tn2 vn), ..., A( t1n v1 + t2n v2 + ...+ tnn vn)) =
=(t11Av1+ t21Av2 + ...+ tn1Avn, t12Av1+ t22Av2 + ...+ tn2vn, ..., t1nAv1+ t2nAv2 + ...+ tnnAvn) =
=(Av1, Av2, ..., Avn)T = (v1, v2, ..., vn)AT = vAT. (2)
Так как левые части равенств (1) и (2) равны, то получаем
v(TB) = vAT. (3)
По лемме следует TB = AT. Так как матрица перехода T от одного базиса векторного пространства невырожденная, то она имеет обратную матрицу T -1, то находим B = T -1 A T.
3. Операции над линейными операторами. Пусть A, B - линейные операторы в векторном пространстве V, A, B - соответственно матрицы линейных операторов A, B относительно одного базиса v.
Определение 1. СуммойA + B линейных операторов A и B векторного пространства V называется отображение V в V, определенное для любого вектора, а из V по формуле: (A + B)а = Aа+ Bа.
Определение 2. Произведение aA числа a на линейный оператор A векторного пространства V называется отображение V в V, определенное для любого вектора, а из V по формуле: (aA)а = a(Aа).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.