Дискретное программирование. Задачи дискретного программирования в САПР. Методы решения задач дискретного программирования, страница 5

(Рекомендуется также ознакомиться с примерами, иллюстрирующими значительное несовпадение «округленного» решения задачи ЛП с решением соответствующей задачи ЦЛП [4,9,10]).

Поэтому для решения задач ЦЛП используются собственные методы, обычно более сложные, чем методы ЛП. Причина этой сложности – в дискретности множества допустимых планов целочисленных задач.

3.4.3.   Методы отсечения

Основная идея методов отсечения состоит в использовании методов решения задачи  ЛП для решения задачи  ЦЛП.

В принципе, такие методы можно было бы использовать, если бы  удалось построить по многограннику задачи ЛП (полученной снятием требований целочисленности) соответствующий целочисленный многогранник  задачи ЦЛП. Тогда, решив для этой области определения  задачу ЛП, мы одновременно получим и решение соответствующей задачи ЦЛП. Однако до настоящего времени алгоритм построения целочисленного  многогранника не найден.

Методы отсечения предусматривают выполнение процедуры последовательного «приближения» к целочисленному многограннику, сопровождающуюся решением вспомогательных задач ЛП.. Такие приближения осуществляются путем последовательного выполнения  так называемых «отсечений» от ОДР задачи ЛП некоторых  подмножеств [4,9].

Сущность алгоритмов, основанных на методе отсечения, можно  уяснить, обратившись к геометрическим представлениям. Пусть ОДР некоторой задачи ЛП приведена на рис. 3.3.

Такая область представляет собой многогранник . Оптимум (максимум) этой задачи достигается в точке B.

Соответствующая задача ЦЛП, получаемая при добавлении требований целочисленности, имеет ОДР, содержащую 16 целочисленных точек. Выпуклая оболочка этого множества, образующая целочисленный многогранник, выделена пунктиром.

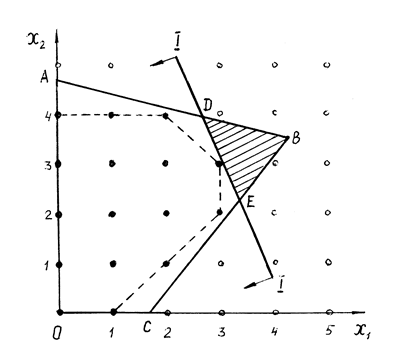
Рис. 3.3.

Предусматриваемые рассматриваемым методом отсечения осуществляются путем введения в задачу целочисленного программирования ограничений, являющихся уравнениями гиперплоскости в пространстве решений и дальнейшего отбрасывания части ОДР задачи ЛП (так, на рисунке 3.3 гиперплоскость  отсекает “верхнюю правую” область от многогранника ).

Далее в соответствии с методом отсечений решается задача ЛП для области 0ADEC0.

При реализации методов «отсечений» возникает ряд проблем. Эти проблемы были впервые решены Гомори. Основой его методов является возможность замены задачи ЦЛП такой задачей ЛП, что ее оптимальное решение совпадает с оптимальным решением задачи ЦЛП.

Гомори был разработан пошаговый алгоритм, позволяющий строить последовательность отсечений и доказана конечность процесса решения задачи. Нами будет рассмотрен первый алгоритм Гомори, разработанный для полностью целочисленной задачи линейного программирования.

Рассмотрим общую схему метода отсечения применительно к полностью целочисленной задаче (имеющей каноническую форму).

 Постановка задачи ЦЛП:

;                                       (3.12)

;                                            (3.13)

;                                            (3.14)

                                    x_j–целые  ,    j =1,…,n                        (3.15)

С ней связана задача ЛП (3.12) - (3.14). Обозначим эти задачи символами  I  и L соответственно. Предположим, что все коэффициенты  - целые числа, область допустимых решений задачи L ограничена, а задача I  имеет допустимое решение.

В соответствии с основной идеей метода требование целочисленности заменяется добавлением новых ограничений, последовательно сужающих допустимую область задачи L, но не затрагивающих точек допустимой области задачи I.

Вначале решается задача  L₀ = L.

Если ее решение удовлетворяет условиям целочисленности, то оно одновременно является и решением  задачи  I.

В противном случае к ограничениям (3.13), (3.14) задачи L добавляется новое линейное ограничение, называемое отсечением (правильным отсечением), которое переводит задачу L₀ в задачу L₁ с допустимой областью, обладающей двумя свойствами. Эти свойства таковы: во-первых, нецелочисленная оптимальная точка задачи L₀ не принадлежит области L₁; во-вторых, все целочисленные точки L₀ сохраняются в допустимой области L₁.