Методы первого порядка. Задачи и методы условной оптимизации нелинейного программирования, страница 7

             4.3 2.  Методы условной оптимизации при ограничениях типа равенств

4.3.2.1. Аналитические методы условной оптимизации при ограничениях типа равенств

Рассмотрим сначала аналитические  методы решения рассматриваемой задачи НП.

Основным методом данной группы является метод множителей Лагранжа, который сводит задачу условной оптимизации вида

z(X) ® min  

g_j (X) = 0,                                                                   (4.39)

i=1,…,m ,  m < n ,                                       

где ограничения заданы равенствами, к задаче безусловной минимизации функции Лагранжа.

В принципе такая задача может быть решена следующим путем. В системе уравнений, задающей ограничения, m независимых переменных x_j выражаются как функции остальных n-m переменных. Далее решается задача безусловной оптимизации функции m выделенных переменных. Однако при сложном виде уравнений возникают серьезные трудности с исключением  n-m переменных.

В связи с этим большое практическое значение метод сведения задачи на условный экстремум к задаче на безусловный экстремум, основанный на использовании функции Лагранжа. Такая функция имеет следующий вид:

                                           L(X, Y) =  z(X) + .                                          (4.40)

В этой функции l_i – неопределенные множители Лагранжа, g_j (X) – функции, задающие левые части ограничений. (Можно сказать, что функция Лагранжа представляет собой сумму целевой функции и суммы произведений множителей Лагранжа на функции ограничения).

Необходимое  условие экстремума такой функции представляется в виде системы n + m уравнений относительно переменных x_j и неопределенных множителей l_i :

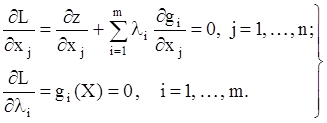                                         (4.41)

Из решения системы (4.41) находится точка (X^*, L^*), которая доставляет минимум функции Лагранжа (4.40) в неограниченной области и одновременно является точкой границы, заданной условиями g_i(x) = 0, i = 1, …, m, где может достигать минимума целевая функция z(X) исходной задачи.

Найденная точка  X^*  является стационарной  точкой функции z(X). В связи с этим необходимо определить характер поведения функции z(X) в окрестности X^* (произвести дополнительное исследование на выпуклость или вогнутость).

Таким образом, задача на условный минимум ЦФ z(X) при наличии ограничений типа равенств сводится к задаче определения стационарных точек функции Лагранжа. В этом случае задача (4.41) решается  аналитическим методом.

Метод множителей Лагранжа может использоваться при решении несложных задач оптимального проектирования. Например, в [53] рассмотрена задача определения размеров параллелепипеда заданного объема, имеющего минимальную поверхность. В [26] рассмотрена аналогичная задача применительно к цилиндру. В [8] приведена задача определения размеров вагонетки, двигающейся по тоннелям с круглым сечением (формально сводящаяся к задаче об определении сторон прямоугольника максимальной площади, вписанного в круг заданного радиуса).

Поскольку  в общем случае система (4.41) является нелинейной, то ее решение может быть достаточно сложной задачей. Отсюда возникает необходимость в численных методах, отыскивающих точку оптимума из решения прямой задачи безусловной минимизации функции Лагранжа (4.40), а не из системы уравнений вида (4.41).

4.3.2.2. Численные методы условной оптимизации при ограничениях типа равенств

Численные методы  условной оптимизации разделяются на две группы:

1)  методы штрафных функций;

2)  методы, учитывающие ограничения в явной форме.

Методы штрафных функций объединяют большую группу методов, использующихся как при ограничениях типа равенств, так и при ограничениях типа неравенств [4,..      ]. Идея этих методов состоит в том, что вместо непосредственного  решения задачи НП с ограничениями (равенствами или неравенствами) переходят к решению последовательности   задач минимизации вспомогательной функции вида