Перейдём теперь к изучению изменения суммы ряда при перестановках его членов. Сначала уточним понятие перестановки. Перестановкой множества натуральных чисел N называется биективное (взаимно однозначное) отображение N на себя:
![]() .
.
Удобно обозначать перестановки
следующим способом: ![]() .
Например,
.
Например, 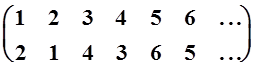 – перестановка, при
которой число 1 переходит в 2, число 2 в 1 и т.д. Теперь для данного
числового ряда
– перестановка, при
которой число 1 переходит в 2, число 2 в 1 и т.д. Теперь для данного
числового ряда  можно
рассматривать ряд
можно
рассматривать ряд
 , состоящий из тех же слагаемых, но
расположенных в другом порядке.
, состоящий из тех же слагаемых, но
расположенных в другом порядке.
Теорема
14. Если ряд ![]() сходится
абсолютно, S – его сумма, то для
любой перестановки
сходится
абсолютно, S – его сумма, то для
любой перестановки ![]() ряд
ряд ![]() тоже абсолютно сходится и имеет ту
же сумму S.
тоже абсолютно сходится и имеет ту
же сумму S.
Доказательство.
Рассмотрим сначала случай, когда ![]() .
Обозначим Sk –
частичные суммы ряда
.
Обозначим Sk –
частичные суммы ряда ![]() ,
, ![]() – частичные суммы ряда
– частичные суммы ряда ![]() . По условию, последовательность {Sk} возрастает и стремится к
конечному пределу S. Пусть
. По условию, последовательность {Sk} возрастает и стремится к
конечному пределу S. Пусть ![]() . Тогда
. Тогда
![]() , так как в Sp есть все слагаемые суммы
, так как в Sp есть все слагаемые суммы ![]() . Так как Sp £ S, то
получаем, что
. Так как Sp £ S, то
получаем, что ![]() – возрастающая
ограниченная сверху последовательность. Значит, она имеет конечный предел
– возрастающая
ограниченная сверху последовательность. Значит, она имеет конечный предел ![]() . То есть ряд
. То есть ряд ![]() сходится и его сумма не может быть
больше суммы исходного ряда . Но, с другой стороны, ряд
сходится и его сумма не может быть
больше суммы исходного ряда . Но, с другой стороны, ряд ![]() тоже получен из ряда
тоже получен из ряда ![]() в результате некоторой перестановки
(обратного отображения
в результате некоторой перестановки
(обратного отображения ![]() ). Поэтому S £ S¢. Следовательно, S¢= S.
). Поэтому S £ S¢. Следовательно, S¢= S.
Теперь
рассмотрим общий случай: слагаемые an
могут иметь произвольные знаки, ряд ![]() абсолютно
сходится. Пусть S+, S– – положительная и отрицательная части
ряда
абсолютно
сходится. Пусть S+, S– – положительная и отрицательная части
ряда ![]() . По теореме 12 S+,
S–
– конечные числа, т.е.
. По теореме 12 S+,
S–
– конечные числа, т.е.
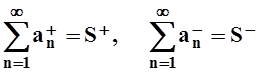
– сходящиеся ряды с положительными членами. Для таких рядов теорема уже доказана, т.е.
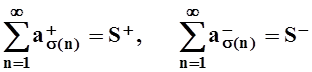 .
.
Так как эти ряды являются
положительной и отрицательной частью ряда ![]() ,
то по теореме 12, ряд
,
то по теореме 12, ряд ![]() абсолютно
сходится, его сумма равна S+ – S–
= S. Теорема доказана.
абсолютно
сходится, его сумма равна S+ – S–
= S. Теорема доказана.
Пример, приведённый в начале раздела, показывает, что для условно сходящихся рядов перестановки слагаемых могут приводить к изменению суммы. Интересно, что этот пример не является исключением, так как справедлива следующая теорема, которую мы приводим без доказательства.
Теорема
15 (теорема Римана). Пусть ряд 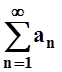 условно сходится. Тогда для любого
числа А существует перестановка
условно сходится. Тогда для любого
числа А существует перестановка ![]() , такая, что сумма ряда
, такая, что сумма ряда ![]() равна А.Кроме того,
существует перестановка, приводящая к расходящемуся ряду.
равна А.Кроме того,
существует перестановка, приводящая к расходящемуся ряду.
13.5 Задачи с решениями
1. Исследовать
сходимость ряда 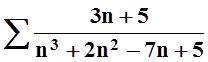 .
.
Решение.
При ![]() (эквивалентные бесконечно
большие последовательности). Поэтому данный ряд должен вести себя так же, как
ряд
(эквивалентные бесконечно
большие последовательности). Поэтому данный ряд должен вести себя так же, как
ряд ![]() . Для уточнения этого
рассуждения применим предельный признак сравнения, сравним наш ряд с рядом
. Для уточнения этого
рассуждения применим предельный признак сравнения, сравним наш ряд с рядом ![]() :
:
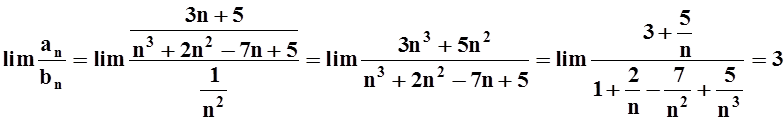 .
.
Так как получилось конечное
ненулевое число, то ряды ведут себя одинаково. Как мы знаем, ряд ![]() сходится. Значит, исследуемый ряд
тоже сходится.
сходится. Значит, исследуемый ряд
тоже сходится.
2. Исследовать
сходимость ряда 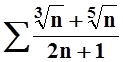 .
.
Решение.
Как и в предыдущем примере, используем предельный признак сравнения. Опять
будем сравнивать с обобщённым гармоническим рядом ![]() при
подходящем a.В числителе максимальная степень n равна
при
подходящем a.В числителе максимальная степень n равна ![]() ,
в знаменателе – 1 . Поэтому
возьмём
,
в знаменателе – 1 . Поэтому
возьмём ![]() . Ряд
. Ряд 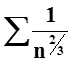 расходится. Вычислим предел:
расходится. Вычислим предел:
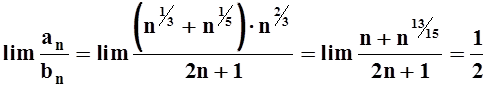 .
.
Так как ![]() , то исследуемый ряд тоже расходится.
, то исследуемый ряд тоже расходится.
3. Исследовать сходимость ряда
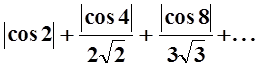 .
.
Решение.
Общий член ряда, очевидно, можно записать так: 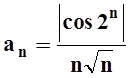 . Ясно, что
. Ясно, что 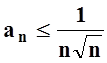 . Ряд
. Ряд 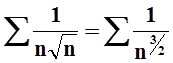 сходится, так как это обобщённый
гармонический ряд с параметром
сходится, так как это обобщённый
гармонический ряд с параметром ![]() . По
признаку сравнения (теорема 5) ряд
. По
признаку сравнения (теорема 5) ряд 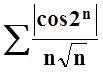 тоже
сходится.
тоже
сходится.
4. Исследовать сходимость ряда
![]() .
.
Решение. Запишем общий член ряда:
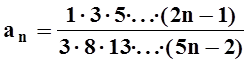 .
.
Применим признак Даламбера. Так как
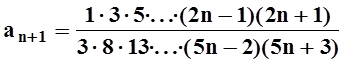 , то
, то 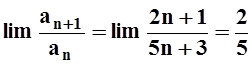 . Предел меньше 1, поэтому ряд сходится.
. Предел меньше 1, поэтому ряд сходится.
5. Исследовать
сходимость ряда 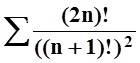 .
.
Решение.
Если в записи общего члена ряда участвует факториал, полезно использовать
признак Даламбера. Так как 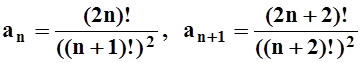 ,
то
,
то
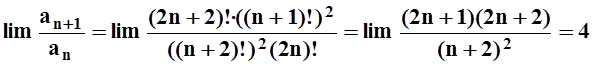 .
.
Предел больше 1, по признаку Даламбера ряд расходится.
6. Исследовать
сходимость ряда 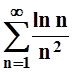 .
.
Решение. Попытаемся применить признак Даламбера:
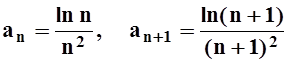 ,
,
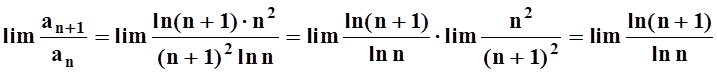 .
.
Вычислим этот предел с помощью предела функции действительной переменной и правила Лопиталя:
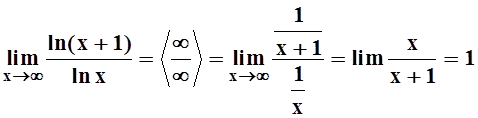 .
.
Из определения предела следует,
что тогда и ![]() . Итак, признак
Даламбера не даёт ответа на вопрос о сходимости. Не очень просто (хотя и можно)
применить здесь признаки сравнения.
. Итак, признак
Даламбера не даёт ответа на вопрос о сходимости. Не очень просто (хотя и можно)
применить здесь признаки сравнения.
Применим
интегральный признак сходимости. Рассмотрим функцию 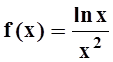 .
Она удовлетворяет всем необходимым требованиям: положительна, непрерывна при
.
Она удовлетворяет всем необходимым требованиям: положительна, непрерывна при ![]() . Чтобы убедиться в том, что f(x) монотонно убывает, вычислим
производную:
. Чтобы убедиться в том, что f(x) монотонно убывает, вычислим
производную:
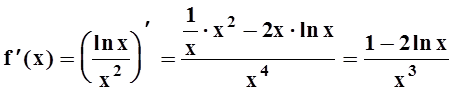 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.