Геометрический подход к изучению функций 2-х и 3-х переменных. Производная по направлению. Градиент скалярного поля, страница 3

Решение.Пусть  F(x, y, z) = y–xz+ln(x–2z).  Найдём частные производные функции   F(x, y, z).

,     ,     .

В достаточно малой окрестности точки  P    x–2z ¹ 0,  поэтому частные производные непрерывны. Кроме того,  . Значит, неявная функция определена. Найдём её частные производные:

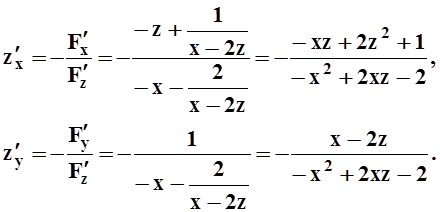
В частности,  ,    .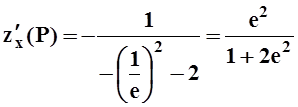

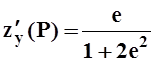5. Найти кратчайшее расстояние между параболой  y = x²+1   и прямой x+y+1 = 0.

Решение.Пусть  (x₁, y₁)  – точка на параболе,  (x₂, y₂)  – точка на прямой. Как известно, расстояние между ними равно .  Требуется найти условный минимум функции S(x₁, x₂, y₁, y₂)  при условиях  ,  x₂+y₂+1 = 0.  Вместо функции  S удобнее рассматривать  S² = (x₁ – x₂)² + (y₁ – y₂)²;  ясно, что эти функции минимальны при одних и тех же значениях переменных.

Для решения задачи на условный экстремум рассмотрим функцию Лагранжа:

.

Найдём стационарные точки, приравнивая  0  все частные производные первого порядка функции  F:

.

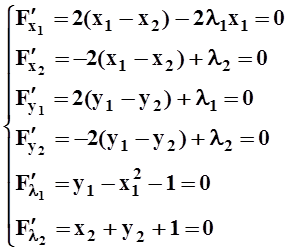Из 3–го и 4–го уравнения следует, что   l₂ = –l₁.  Учитывая это и складывая первые 2 уравнения, получим:  2l₁x₁+l₁ = 0.  Так как  l₁ ¹ 0  (иначе  x₁ = x₂,  y₁ = y₂,  а это невозможно, парабола и прямая не пересекаются), то получаем .  Значит,  .  Теперь достаточно использовать 1, 3 и 6 уравнения:

.

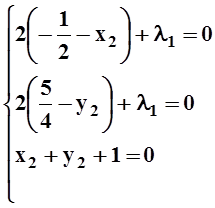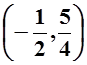Из первых уравнений следует:  ,  т. е. .  Подставляя    в последнее уравнение, получим:  ,  ,  .  Значит .  Итак, стационарная точка только одна:  , ,  ,  .   Из геометрического смысла задачи следует, что условный минимум существует. В других точках он достигаться не может. Поэтому ясно, что минимальное расстояние равно расстоянию между точками    и  , достаточные условия минимума можно не проверять.

Найдём кратчайшее расстояние:

.

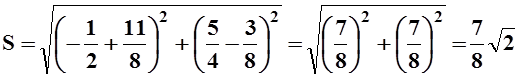6. В точке  P(3,3)  найти градиент функции  ,  а также производную этой функции в направлении градиента.

Решение.Найдем частные производные в точке  P:

;   .

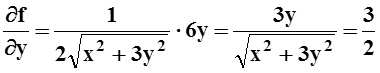Значит, градиент   .

Производная по направлению градиента равна модулю градиента:

.

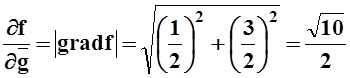7.  Найти  уравнение  касательной,  проведённой  в  точке   (π–2, 2)   к  циклоиде     x = 2(t–sint),  y= 2(1–cost).

Решение.Решая систему уравнений

, находим    – значение параметра, соответствующее данной точке. Направляющий вектор касательной

.

Получаем уравнение касательной:  ,  или  y = x+4–p.   Конечно, тот же результат мы бы получили, находя угловой коэффициент касательной с помощью производной:  .

8. Найти уравнение касательной в точке   к линии пересечения сферы  x²+y²+z² = 4  и цилиндра   x²+y² = 2x  (кривая Вивиани).

Решение.Чтобы найти направляющий вектор касательной, нужно перейти к параметрическому заданию линии. Возьмём в качестве параметра абсциссу  x.  Для определения  ,    можно не выражать  y  и  z  через  x,  а дифференцировать как неявные функции:

В точке   получаем:  ,  y¢= 0.  Так как  x¢= 1,  то получаем направляющий вектор касательной:

.

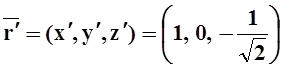Можно взять в качестве направляющего, конечно, и вектор  . Поэтому канонические уравнения касательной имеют вид:

.

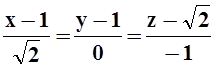Замечание.   Ординату  y  нельзя было взять в качестве параметра, так как уравнение  x²+y² = 2x    не определяет в  окрестности  точки       неявно  функцию   x(y):    в этой точке.

10.7   Упражнения для самостоятельной работы

1.  Разложить по формуле Тейлора в окрестности точки  (0,0)  до членов 2–го порядка функции:

а)  f(x,y) = ln(1+x+y);                 б)   .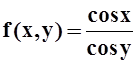

2.  Исследовать на экстремум функции:

а)  z = x³–x²y–3lny;                     б)  z = x³+8y²–6xy;

в)  z = (x–3)²–(y+5)²;                  г)  z = 5x²+y²+2x³–xy²;

д)  ;                   е)  z = x⁴+y³–3xy².

3.  Найти наибольшее и наименьшее значение функции на ограниченном замкнутом множестве  D.