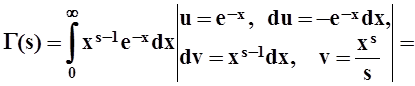
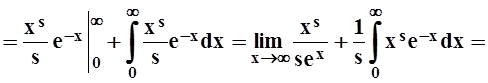
![]() .
.
Итак,
Г(s+1)= s Г(s).
Отсюда следует, что
Г(s+2)= (s+1)×s×Г(s),
………………………………………
Г(s+n)= (s+n–1)(s+n–2)...(s+1)s×Г(s).
В частности, при s = 1 получаем:
Г(n+1)= n!Г(1).
Значение Г(1) легко вычислить:
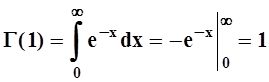 .
.
Поэтому Г(n+1)= n!. Мы получили, что дифференцируемая функция Г(s) является продолжением факториала (определённого лишь для натуральных чисел) на множество всех положительных действительных чисел.
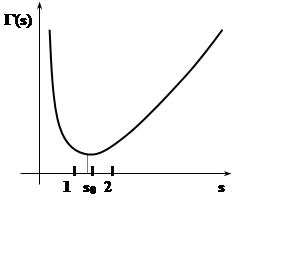
Так как Г(2) = Г(1) = 1, то, по теореме Ролля, на отрезке [1, 2] есть точка, где производная обращается в 0. Вторая производная, очевидно, во всех точках положительна
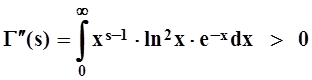
(так как подинтегральная функция положительна). Значит, точка s0, где Г¢(s0)= 0, является точкой минимума. Можно вычислить:
s0 = 1,4616...., Г(s0)= 0,8856... .
График функции Г(s) имеет следующий вид:
 |
![]() .
.
В частности, при ![]() :
:
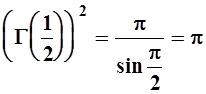 , т.е.
, т.е. 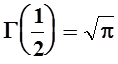 .
.
Формула Г(s+1)= sГ(s) и формула
дополнения позволяют выразить любое значение гамма–функции
через её значения на отрезке ![]() .
Для использования Г–функции
в практических расчётах составлены подробные таблицы.
.
Для использования Г–функции
в практических расчётах составлены подробные таблицы.
16.4 Задачи с решениями
1. Найти
производную функции 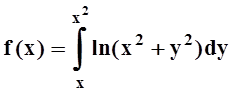 .
.
Решение. Здесь от параметра х зависит не только подинтегральная функция, но и пределы интегрирования. Поэтому применяем формулу, выведенную в теореме 5:
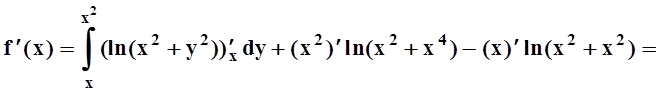
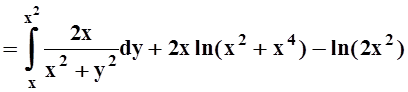 .
.
В данном случае можно вычислить интеграл и записать ответ в явном виде:
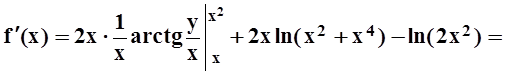
![]()
![]() .
.
2. Вычислить
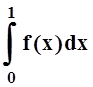 , если
, если 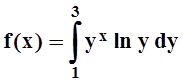 .
.
Решение. Так как подинтегральная функция непрерывна на прямоугольнике [0,1] ´ [1,3] , то можно изменить порядок интегрирования:
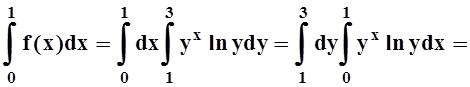
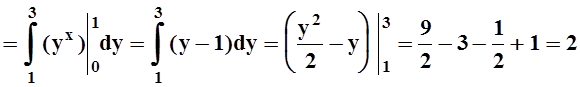 .
.
3. Доказать
что несобственный интеграл 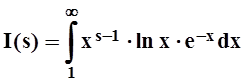 равномерно сходится на отрезке [0, 1].
равномерно сходится на отрезке [0, 1].
Решение. Так как ln x < x, то при x³1
xs–1×lnx×e–x < xse–x £ x e–x.
Интеграл 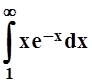 сходится:
сходится:
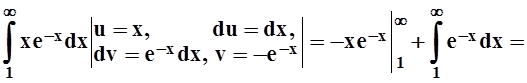
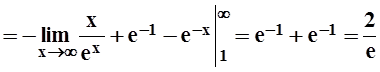 .
.
Значит,
интеграл 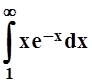 является мажорирующим для I(s). По признаку
Вейерштрасса, I(s) равномерно сходится.
является мажорирующим для I(s). По признаку
Вейерштрасса, I(s) равномерно сходится.
4. Вычислить
интеграл 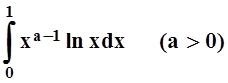 .
.
Решение.
Интеграл является несобственным с особенностью в точке х= 0: при х®0 неограничен
и логарифм, и функция xa–1 (при a < 1).
Рассмотрим интеграл 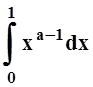 . Он сходится и легко
вычисляется:
. Он сходится и легко
вычисляется: 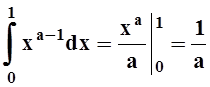 . Искомый интеграл можно
получить из этого путём дифференцирования по параметру а. Однако, чтобы применить теорему 9, нужно
убедиться в равномерной сходимости интеграла
. Искомый интеграл можно
получить из этого путём дифференцирования по параметру а. Однако, чтобы применить теорему 9, нужно
убедиться в равномерной сходимости интеграла 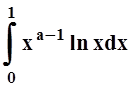 .
Докажем, что этот интеграл равномерно сходится на
любом промежутке [a0,¥),
где a0 > 0.
Для этого следует найти мажорирующий сходящийся интеграл. Заметим: так как xÎ(0,
1), то
.
Докажем, что этот интеграл равномерно сходится на
любом промежутке [a0,¥),
где a0 > 0.
Для этого следует найти мажорирующий сходящийся интеграл. Заметим: так как xÎ(0,
1), то
| ![]() ln x|
£
ln x|
£ ![]() | ln x|.
| ln x|.
Теперь нужно доказать, что
интеграл 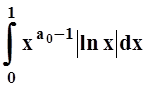 сходится. Сравним его с
сходится. Сравним его с 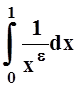 , где число eÎ(1–a0,
1) . Вычислим предел:
, где число eÎ(1–a0,
1) . Вычислим предел:
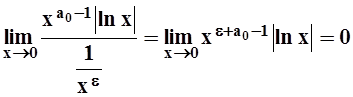
(степень x положительна, неопределённость 0×¥ легко раскрывается по правилу Лопиталя). Следовательно, при малых х
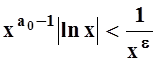 , а интеграл
, а интеграл 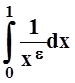 сходится. Поэтому
сходится. Поэтому 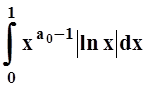 сходится. Значит,
сходится. Значит, 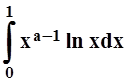 сходится равномерно и можно
применить теорему 9:
сходится равномерно и можно
применить теорему 9:
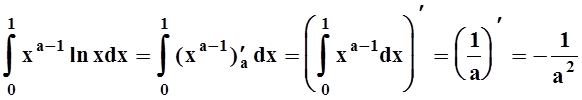 .
.
5. Вычислить
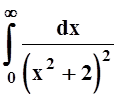 .
.
Решение.
Рассмотрим интеграл, зависящий от параметра: 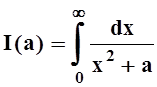 .
Он легко вычисляется:
.
Он легко вычисляется: 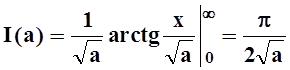 . Применим к
нему теорему о дифференцировании по параметру:
. Применим к
нему теорему о дифференцировании по параметру:
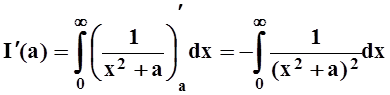 .
.
С другой стороны
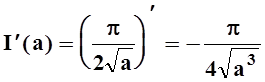 . Значит,
. Значит,
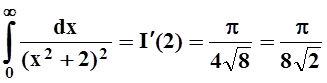 .
.
Дифференцирование по параметру
законно, так как при a> 0 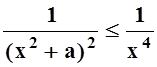 , и сходящийся интеграл
, и сходящийся интеграл 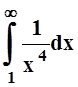 является мажорирующим
для
является мажорирующим
для 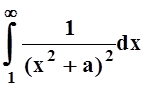 . Поэтому
. Поэтому 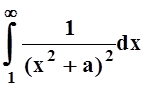 , а следовательно и
, а следовательно и 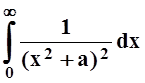 , сходятся равномерно.
, сходятся равномерно.
6. Вычислить
интеграл Эйлера – Пуассона 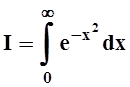 .
.
Решение. Сделаем замену переменной: x = ut, где u > 0 – параметр. Тогда
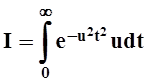 .
.
Умножим это равенство на ![]() и
проинтегрируем в пределах от 0 до ¥:
и
проинтегрируем в пределах от 0 до ¥:
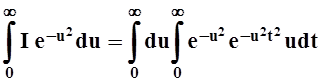 .
.
Левая часть: 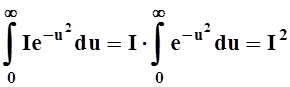 . Вычисляем
правую часть, изменяя порядок интегрирования:
. Вычисляем
правую часть, изменяя порядок интегрирования:
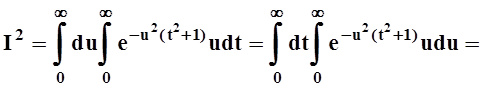
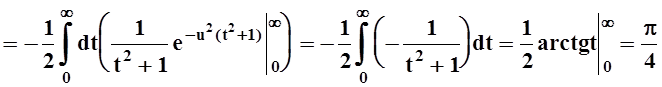 .
.
Следовательно, 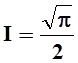 . Правомерность изменения порядка
интегрирования оставляем здесь без доказательства.
. Правомерность изменения порядка
интегрирования оставляем здесь без доказательства.
7. Вычислить
![]() , не используя формулу дополнения
для гамма–функции.
, не используя формулу дополнения
для гамма–функции.
Решение. Сделаем замену переменной:
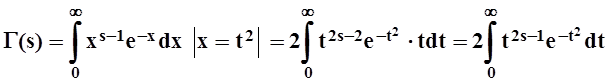 .
.
Подставим ![]() и воспользуемся интегралом Эйлера
– Пуассона:
и воспользуемся интегралом Эйлера
– Пуассона:
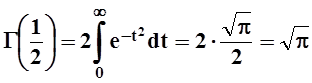 .
.
16.5 Упражнения для самостоятельной работы
1. Вычислить пределы:
а) 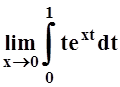 ; б)
; б) 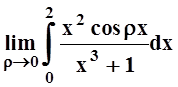 ;
;
в) 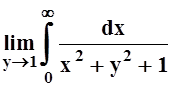 ; г)
; г) 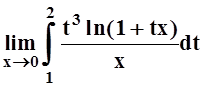 .
.
2. Найти производную функции:
а) 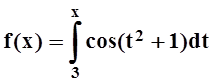 ; б)
; б) 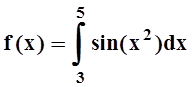 ;
;
в) 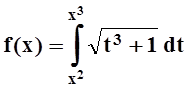 ; г)
; г) 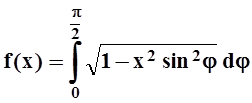 ;
;
д) 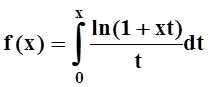 ; е)
; е) 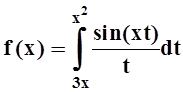 .
.
3. Найти 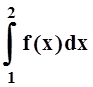 ,
если
,
если 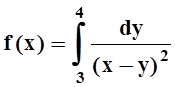 .
.
4. Найти 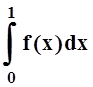 , если
, если 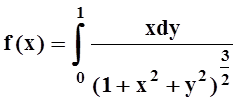 .
.
5. Доказать,
что интеграл 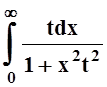 равномерно сходится на
отрезке [3,5].
равномерно сходится на
отрезке [3,5].
6. Доказать,
что интеграл 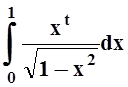 равномерно сходится на [0, ¥).
равномерно сходится на [0, ¥).
7. Вычислить 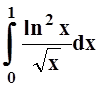 . Указание: см. задачу 4 из 16.4.
. Указание: см. задачу 4 из 16.4.
8. Вычислить 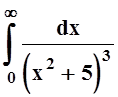 . Указание:
см. задачу 5 из 16.4.
. Указание:
см. задачу 5 из 16.4.
16.6 Образец теста
(для дистанционной формы обучения)
1. Найти
значение f(p), если 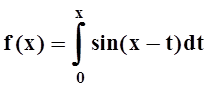 .
.
2. Найти 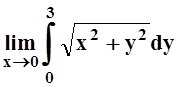 .
.
3. Вычислить f¢(0),
если 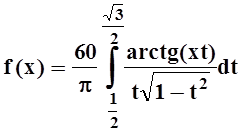 .
.
4. Вычислить 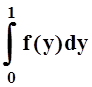 , если
, если 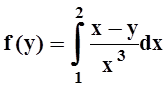 .
.
5.
Несобственный интеграл 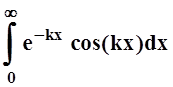 на отрезке [1,
2] 1) сходится
равномерно; 2) сходится, но не равномерно; 3) расходится в
некоторых точках этого отрезка. Указать номер
истинного высказывания.
на отрезке [1,
2] 1) сходится
равномерно; 2) сходится, но не равномерно; 3) расходится в
некоторых точках этого отрезка. Указать номер
истинного высказывания.
6. Вычислить Г(5).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.