Направляющие косинусы вектора единичной нормали:
cos a=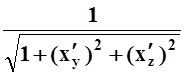 , cos b=
, cos b=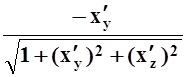 , cos g=
, cos g=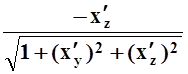 . Вычисляем интеграл:
. Вычисляем интеграл:
![]() ydxdz +
(1 + xz)dydz =
ydxdz +
(1 + xz)dydz =![]() [(1 + xz)
cos a+ y cos b+ 0×cos g] ds=
[(1 + xz)
cos a+ y cos b+ 0×cos g] ds=
 =
=![]() (1 + xz)
cos a ds=
(1 + xz)
cos a ds=![]() (1 + z
(1 + z![]() )dydz.
)dydz.
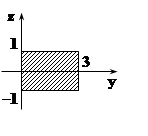
Проекция S на плоскость YOZ – прямоугольник, двойной интеграл легко вычисляется:
![]() (1
+z
(1
+z![]() )dydz=
)dydz= ![]() dz
dz![]() (1 +z
(1 +z![]() )dy=
)dy=
=3![]() (1 +z
(1 +z![]() )dz=
)dz= 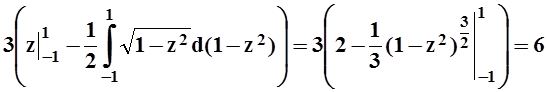 .
.
5.
Найти поток векторного поля ![]() =x2
=x2![]() +y2
+y2![]() через
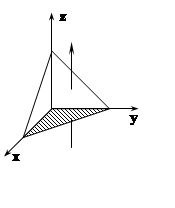
внешнюю сторону поверхности пирамиды, ограниченной плоскостями x= 0, y= 0, z= 0, x+y+z=1.
через
внешнюю сторону поверхности пирамиды, ограниченной плоскостями x= 0, y= 0, z= 0, x+y+z=1.
Решение. Так как поверхность замкнутая, то можно воспользоваться формулой Гаусса – Остроградского:
P= ![]() x2dydz+y2dxdz=
x2dydz+y2dxdz=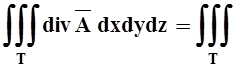 (2x+ 2y)dxdydz, где T – пирамида. Вычисляем тройной интеграл:
(2x+ 2y)dxdydz, где T – пирамида. Вычисляем тройной интеграл:
![]() (2x+ 2y)dxdydz= 2
(2x+ 2y)dxdydz= 2![]() dxdy
dxdy![]() (x+y)dz=
(x+y)dz=
= 2![]() (x+y)(1
–x–y)dxdy= 2
(x+y)(1
–x–y)dxdy= 2![]() dx
dx![]() ((x+y) – (x+y)2)dy=
((x+y) – (x+y)2)dy=
= 2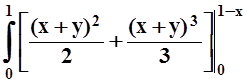 dx= 2
dx= 2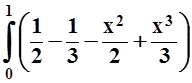 dx=
dx=
= 2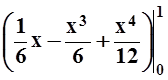 = 2
= 2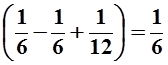 .
.
6.
Найти в точке M(1, 2, 3) дивергенцию и ротор векторного
поля 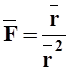 , где
, где ![]() =x
=x![]() +y
+y![]() +z
+z![]() .
.
Решение.
![]() 2
– скалярный квадрат вектора
2
– скалярный квадрат вектора ![]() :
: ![]() 2= (
2= (![]() ,
, ![]() ) =x2+y2+z2. Поэтому
) =x2+y2+z2. Поэтому
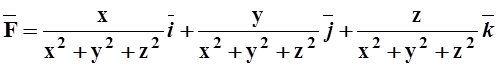 .
.
Вычислим дивергенцию, используя формулу теоремы 7:
div![]() =
= 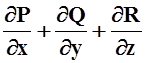 =
=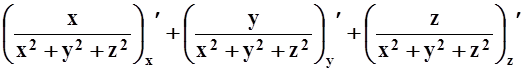 =
=
=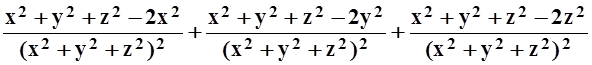 =
= 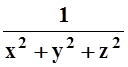 .
.
В частности, в точке M: div![]() (M) =
(M) =![]() .
.
Вычислим rot![]() , используя
определение ротора:
, используя
определение ротора:
rot![]() =
=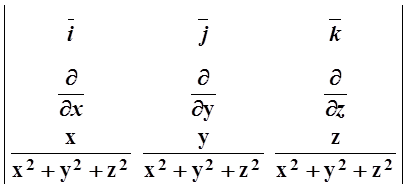 =
=
=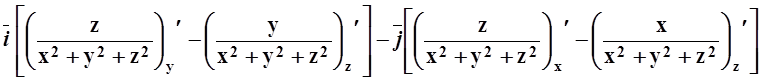 +
+
+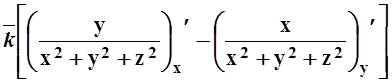 = 0
= 0![]() + 0
+ 0![]() + 0
+ 0![]() =
= ![]() .
.
Значит, поле потенциально – ротор во всех точках равен нулю.
12.5 Упражнения для самостоятельной работы
1. Вычислить криволинейные интегралы 2 рода:
а) ![]() (x2+ 1)y2dx+
(x2+ 1)y2dx+![]() dy; G – дуга
кривой y=
dy; G – дуга
кривой y=![]() от
точки A(0, 1)
до точкиB(–1,
от
точки A(0, 1)
до точкиB(–1,
![]() );
);
б) ![]() ydx+
ydx+![]() dy;
G –
дуга кривой y=ex от точки A(0,
1) до точки B(1,
e);
dy;
G –
дуга кривой y=ex от точки A(0,
1) до точки B(1,
e);
в) ![]() (x+z)dx+ (y–x)dy+ (z+2y)dz; G – отрезок прямой
(x+z)dx+ (y–x)dy+ (z+2y)dz; G – отрезок прямой ![]() от точки A(– 5, 0,
1) до точки B(1,
4, –
1).
от точки A(– 5, 0,
1) до точки B(1,
4, –
1).
2. Вычислить
криволинейный интеграл ![]() (x–y)dx+ (2x+ 3y)dy,
если A(1, 0),
B(0, 1),
а интегрирование проводится а) по прямой; б) по
окружности x2+y2= 1.
(x–y)dx+ (2x+ 3y)dy,
если A(1, 0),
B(0, 1),
а интегрирование проводится а) по прямой; б) по
окружности x2+y2= 1.
3. Вычислить
циркуляцию векторного поля ![]() = (3x+ 5y)
= (3x+ 5y)![]() +(2x–y)
+(2x–y)![]() :
:
а) вдоль окружности x= 2 cost, y= 2 sint;
б) вдоль окружности (x– 3)2 + (y+ 7)2 = 25.
4. Вычислить
циркуляцию векторного поля ![]() =(3x+2y)
=(3x+2y)![]() +(5x–2y)
+(5x–2y)![]() +(3z–y2)
+(3z–y2)![]() вдоль
линии пересечения поверхностей x2+y2=z2, z= 2.
Направление обхода – по часовой стрелке, если смотреть из начала координат.
вдоль
линии пересечения поверхностей x2+y2=z2, z= 2.
Направление обхода – по часовой стрелке, если смотреть из начала координат.
5. Найти
работу векторного поля 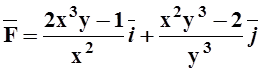 по перемещению
точки из положения A(1, 1)
в положение B(4, 2).
Зависит ли работа от траектории движения точки?
по перемещению
точки из положения A(1, 1)
в положение B(4, 2).
Зависит ли работа от траектории движения точки?
6. Найти функцию U(x,y), если известен её дифференциал:
а) dU=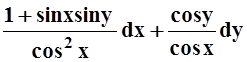 ;
;
б) dU=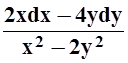 .
.
7. Проверить, что данное векторное поле является потенциальным и найти его потенциал:
а) 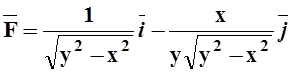 ; б)
; б) ![]() ;
;
в) 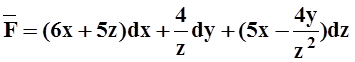 ; г)
; г) 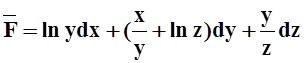 .
.
8. Вычислить поверхностный интеграл 2 рода
![]() (2x+y)dydz+ 2zdxdz+ (4z+9x+5)dxdy, где S¢–
верхняя сторона части плоскости 3x– 2y– 2z+ 6 = 0, соответствующей значениям x£ 0, y³ 0, z³ 0.
(2x+y)dydz+ 2zdxdz+ (4z+9x+5)dxdy, где S¢–
верхняя сторона части плоскости 3x– 2y– 2z+ 6 = 0, соответствующей значениям x£ 0, y³ 0, z³ 0.
9. Вычислить
поверхностный интеграл ![]() x2dydz+y2dxdz,
если S¢– нижняя сторона части поверхности z=x2, проекция которой на плоскость XOY есть треугольник с вершинами (0, 0),
(1, 1), (
x2dydz+y2dxdz,
если S¢– нижняя сторона части поверхности z=x2, проекция которой на плоскость XOY есть треугольник с вершинами (0, 0),
(1, 1), (![]() , 1).
, 1).
10. Вычислить поверхностный интеграл
![]() (7x+5y)dydz+ (8x–y)dxdz+ (3xy–2z–2)dxdy, если S¢– внешняя сторона замкнутой поверхности,
образованной поверхностями x2+y2= (z+ 1)2,
z=– 3.
(7x+5y)dydz+ (8x–y)dxdz+ (3xy–2z–2)dxdy, если S¢– внешняя сторона замкнутой поверхности,
образованной поверхностями x2+y2= (z+ 1)2,
z=– 3.
11. Найти
поток векторного поля ![]() через нижнюю сторону
нижней половины сферы x2+y2 +z2 =R2.
через нижнюю сторону
нижней половины сферы x2+y2 +z2 =R2.
12. Найти
поток векторного поля ![]() через внешнюю сторону
полной поверхности призмы, ограниченной плоскостями x= 0, y= 0, z = 0, z = 1,x+y=1.
через внешнюю сторону
полной поверхности призмы, ограниченной плоскостями x= 0, y= 0, z = 0, z = 1,x+y=1.
13. Найти
поток векторного поля ![]() через внешнюю сторону
сферы (x– 3)2+ (y+ 1)2 + (z– 5)2 =1.
через внешнюю сторону
сферы (x– 3)2+ (y+ 1)2 + (z– 5)2 =1.
14. Найти
поток векторного поля ![]() через внешнюю сторону
части поверхности цилиндра x2+y2 =1, соответствующей значениям y³ 0, 0 £z£ 1.
через внешнюю сторону
части поверхности цилиндра x2+y2 =1, соответствующей значениям y³ 0, 0 £z£ 1.
15. Найти дивергенцию и ротор векторного поля в указанной точке M:
а) ![]() , M(2,
3, 7);
, M(2,
3, 7);
б) ![]() , M(– 1, 1,
3);
, M(– 1, 1,
3);
в) 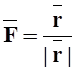 , где
, где ![]() ;
M(1, 2,
2);
;
M(1, 2,
2);
г) ![]() ; M(x0, y0, z0).
; M(x0, y0, z0).
16. Вычислить
ротор векторного поля ![]() =j×gradj, где j=j(x,
y, z)
– произвольная функция.
=j×gradj, где j=j(x,
y, z)
– произвольная функция.
17. В точке M(4,
0, –
4) вычислить дивергенцию поля ![]() , где
, где ![]() – постоянный вектор длины 5, образующий с радиусом–вектором точки M угол
– постоянный вектор длины 5, образующий с радиусом–вектором точки M угол ![]() .
.
12.6 Образец теста
(для дистанционной формы обучения)
1. Найти
работу, совершаемую силой ![]() по перемещению
точки из положения A(0, 0) в
положение B(2, 8) вдоль
кривой y=x3.
по перемещению
точки из положения A(0, 0) в
положение B(2, 8) вдоль
кривой y=x3.
2. При каком
значении параметра a поле 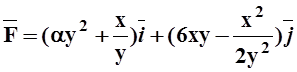 является
потенциальным?
является
потенциальным?
3. Вычислить
поток векторного поля ![]() через внешнюю сторону
полной поверхности куба, ограниченного плоскостями x= 0, y= 0, z
= 0, x = 2, y = 2,z=2.
через внешнюю сторону
полной поверхности куба, ограниченного плоскостями x= 0, y= 0, z
= 0, x = 2, y = 2,z=2.
4. Вычислить
дивергенцию поля ![]() в точке (1, 1,
1).
в точке (1, 1,
1).
5. Найти
модуль ротора поля 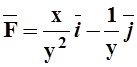 в точке (
в точке (![]() , 1, 5).
, 1, 5).
6. Какое из перечисленных векторных полей является соленоидальным?
1) y sin z ![]() + x
+ x![]() + cos z
+ cos z ![]() ; 2) y sin z
; 2) y sin z ![]() – cos y
– cos y ![]() ;
;
3) x cos z ![]() + sin (x +
z)
+ sin (x +
z)![]() – sin z
– sin z ![]() ; 4) z
sin y
; 4) z
sin y ![]() + x sin z
+ x sin z ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.