 Решение.
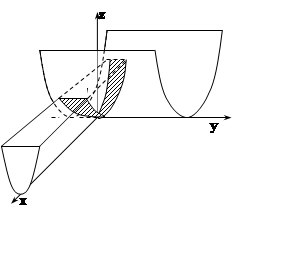
Сделаем чертёж. Поверхность x2 = 2z – цилиндрическая, её направляющая – парабола x2 = 2z в
плоскости XOZ, а образующие
параллельны оси OY. Аналогично
строится цилиндрическая поверхность z= y2, которая, вместе с
плоскостью z= 2, вырезает из поверхности x2 = 2z две симметричные части S1 и S2. Удобно проецировать их
на плоскость YOZ, хотя и придётся
рассматривать только одну из частей (иначе проекция не будет однозначной).
Рассматриваем часть S1, соответствующую
положительным x:
Решение.
Сделаем чертёж. Поверхность x2 = 2z – цилиндрическая, её направляющая – парабола x2 = 2z в
плоскости XOZ, а образующие
параллельны оси OY. Аналогично
строится цилиндрическая поверхность z= y2, которая, вместе с
плоскостью z= 2, вырезает из поверхности x2 = 2z две симметричные части S1 и S2. Удобно проецировать их
на плоскость YOZ, хотя и придётся
рассматривать только одну из частей (иначе проекция не будет однозначной).
Рассматриваем часть S1, соответствующую
положительным x: ![]() . Тогда
. Тогда 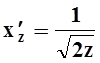 ,
, ![]() и
мы получаем:
и
мы получаем:
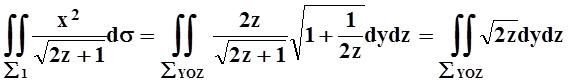 .
.
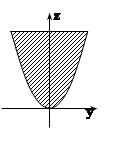 Проекция SYOZ ограничена параболой z = y2 и
прямой z = 2.Вычислим полученный двойной интеграл:
Проекция SYOZ ограничена параболой z = y2 и
прямой z = 2.Вычислим полученный двойной интеграл:
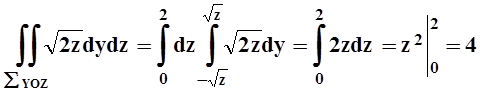 .
.
Поверхность S2 задана уравнением ![]() , имеет ту
же проекцию. Подинтегральная функция и выражение для dsпринимают в симметричных точках S1 и S2 одинаковые значения. Поэтому
, имеет ту
же проекцию. Подинтегральная функция и выражение для dsпринимают в симметричных точках S1 и S2 одинаковые значения. Поэтому
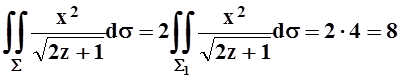 .
.
11.5 Геометрические и физические приложения интегралов
Основные геометрические приложения интегралов уже рассмотрены: если подинтегральная функция тождественно равна 1, то интеграл равен «мере» фигуры, по которой он вычисляется. Итак, площадь плоской фигуры Е:
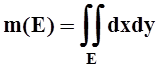 ;
;
объём трёхмерного тела Т:
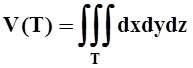 ;
;
длина кривой Г (плоской или пространственной):
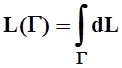 ;
;
площадь поверхности S:
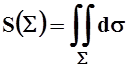 .
.
 Тип
интеграла определяется типом фигуры.
Тип
интеграла определяется типом фигуры.
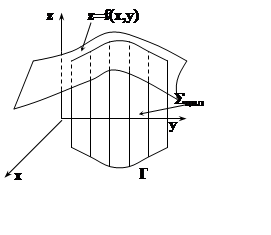
Ещё одно геометрическое приложение имеет криволинейный интеграл 1 рода по плоской кривой. Он даёт площадь части цилиндрической поверхности Sцил (её образующие параллельны оси OZ, направляющая – кривая Г в плоскости XOY), заключённой между плоскостью XOY и поверхностью z = f(x, y)(f(x, y)³0):
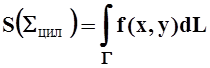 .
.
Действительно, если в
интегральной сумме криволинейного интеграла ![]() заменить
заменить
![]() на длины звеньев вписанной ломаной,
то получим площадь многогранной фигуры, составленной из прямоугольников. Можно
доказать, что при измельчении разбиений площадь такой фигуры стремится к
площади цилиндрической поверхности.
на длины звеньев вписанной ломаной,
то получим площадь многогранной фигуры, составленной из прямоугольников. Можно
доказать, что при измельчении разбиений площадь такой фигуры стремится к
площади цилиндрической поверхности.
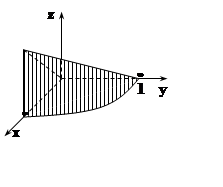
Пример 9. Найти площадь части цилиндрической поверхности y= 1–x2, расположенной в первом октанте между плоскостями z= 0 и z= x.
 Решение.
Направляющая Г рассматриваемой
цилиндрической поверхности – участок параболы y= 1–x2,0£x£1. Вычисляем площадь с помощью
криволинейного интеграла:
Решение.
Направляющая Г рассматриваемой
цилиндрической поверхности – участок параболы y= 1–x2,0£x£1. Вычисляем площадь с помощью
криволинейного интеграла:
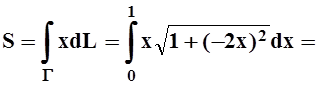
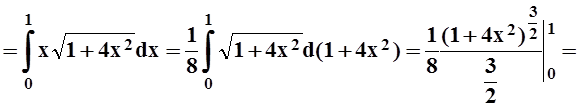
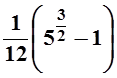 .
.
И геометрические, и физические приложения интегралов всегда связаны с вычислением некоторой величины Q, относящейся к данной фигуре (фигура может быть плоской, пространственным телом, кривой или поверхностью). Величина Q должна обладать свойством аддитивности, т.е. при разбиении фигуры величина, относящаяся по всей фигуре должна равняться сумме величин, относящихся к элементам разбиения. Хорошим примером является масса. Масса всей фигуры, конечно, равна сумме масс её частей. Задача вычисления массы для случая тонкого стержня подробно рассмотрена в 7.5.4. Масса любой фигуры также равна интегралу (соответствующего типа) по этой фигуре от функции плотности.
Пример 10. Найти массу полушара x2+y2+z2 £ R2, 0£z£R, если плотность в каждой точке пропорциональна аппликате этой точки.
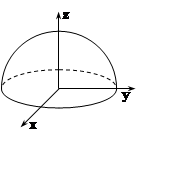 Решение.
В задаче речь идёт о пространственном теле Т; значит, применяется тройной
интеграл. По условию плотность
Решение.
В задаче речь идёт о пространственном теле Т; значит, применяется тройной
интеграл. По условию плотность ![]() , где k–
коэффициент пропорциональности. Тип интеграла и подинтегральная функция
определены, осталось провести вычисления.
, где k–
коэффициент пропорциональности. Тип интеграла и подинтегральная функция
определены, осталось провести вычисления.
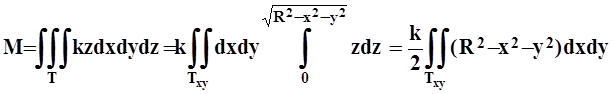 .
.
Проекция Тxy есть круг, поэтому лучше перейти в полярную систему координат.
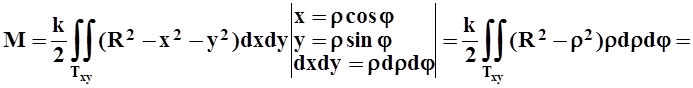
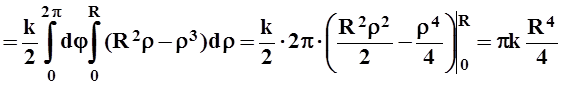 .
.
Ещё
одна аддитивная величина, играющая важную роль в механике – статический момент.
Рассмотрим сначала это понятие для объектов на плоскости. Статическим
моментом материальной точки относительно некоторой оси называется
произведение md, где m–
масса точки, d–расстояние до оси. Для системы точек
на плоскости с массами m1,
m2, ..., mn статистический момент равен 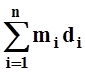 , причём расстояния di берутся со знаком «+» для точек, лежащих по одну сторону от оси,
и со знаком «–» для точек, лежащих по
другую сторону.
, причём расстояния di берутся со знаком «+» для точек, лежащих по одну сторону от оси,
и со знаком «–» для точек, лежащих по
другую сторону.
 Распространим
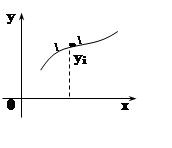
это понятие на произвольную материальную фигуру Е на плоскости (это может быть плоская область или плоская
кривая). Момент будем рассматривать относительно одной из координатных осей,
например, OX. Пусть распределение
массы задано функцией плотности r=r(x,y).
Рассмотрим разбиение фигуры, выберем точку (xi,yi) в каждом элементе Еi. Масса элемента Еi приближённо равна r(xi,yi)m(Ei) (здесь m(Ei)
– площадь или длина, в зависимости от фигуры). Статический момент элемента Еi приближённо равен:
Распространим
это понятие на произвольную материальную фигуру Е на плоскости (это может быть плоская область или плоская
кривая). Момент будем рассматривать относительно одной из координатных осей,
например, OX. Пусть распределение
массы задано функцией плотности r=r(x,y).
Рассмотрим разбиение фигуры, выберем точку (xi,yi) в каждом элементе Еi. Масса элемента Еi приближённо равна r(xi,yi)m(Ei) (здесь m(Ei)
– площадь или длина, в зависимости от фигуры). Статический момент элемента Еi приближённо равен:
![]()
(мы считаем, что масса сосредоточена в выбираемой точке). Суммируя, получаем:
![]() .
.
Переходя к пределу по всё более мелким разбиениям, находим точное выражение для статического момента через интеграл:
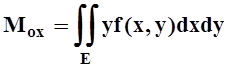 , если Е – плоская пластина;
, если Е – плоская пластина;
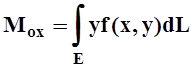 , если Е – кривая.
, если Е – кривая.
Заметим, что эти равенства являются определениями статических моментов для соответствующих фигур.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.