Условие независимости криволинейного интеграла от пути можно сформулировать, используя понятие циркуляции.
Теорема 3.
Интеграл ![]() Pdx+Qdy не зависит от пути Û для любого замкнутого
контура L
Pdx+Qdy не зависит от пути Û для любого замкнутого
контура L ![]() Pdx+Qdy= 0.
Pdx+Qdy= 0.
 Доказательство. «
Þ ».
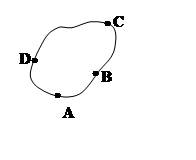
Возьмём на замкнутом контуре L
произвольно 4 точки (см. рисунок). По условию
Доказательство. «
Þ ».
Возьмём на замкнутом контуре L
произвольно 4 точки (см. рисунок). По условию
![]() Pdx+Qdy=
Pdx+Qdy=![]() Pdx+Qdy.
Pdx+Qdy.
Пользуясь этим,
получим: ![]() Pdx+Qdy=
Pdx+Qdy=
=![]() Pdx+Qdy+
Pdx+Qdy+![]() Pdx+Qdy=
Pdx+Qdy=![]() Pdx+Qdy–
Pdx+Qdy–![]() Pdx+Qdy= 0.
Pdx+Qdy= 0.
« Ü ». Возьмём две различные кривые ABC и ADC, начало и конец которых совпадают. По условию, интеграл по замкнутому контуру ABCDA равен нулю:
0 =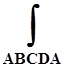 Pdx+Qdy=
Pdx+Qdy=![]() Pdx+Qdy+
Pdx+Qdy+![]() Pdx+Qdy=
Pdx+Qdy=
=![]() Pdx+Qdy–
Pdx+Qdy–![]() Pdx+Qdy.
Pdx+Qdy.
Значит ![]() Pdx+Qdy=
Pdx+Qdy=![]() Pdx+Qdy, что и требовалось доказать.
Pdx+Qdy, что и требовалось доказать.
Мы получили несколько условий потенциальности
плоского векторного поля. Однако ни одно из них не позволяет проверить:
является ли потенциальным данное векторное поле P(x,y)![]() +Q(x,y)
+Q(x,y)![]() ? Для такой проверки удобно использовать
признак полного дифференциала, который мы сейчас рассмотрим. Но сначала дадим
определение односвязной области. Область E (на плоскости) называется односвязной, если
для любого замкнутого контура L,
лежащего в E, часть
плоскости, ограниченная L,
является подмножеством в E.
? Для такой проверки удобно использовать
признак полного дифференциала, который мы сейчас рассмотрим. Но сначала дадим
определение односвязной области. Область E (на плоскости) называется односвязной, если
для любого замкнутого контура L,
лежащего в E, часть
плоскости, ограниченная L,
является подмножеством в E.

Односвязная область Неодносвязная область
Можно объяснить, что такое односвязная область несколько по–другому. Любой замкнутый контур, лежащий в односвязной области, можно, непрерывно изменяя, стянуть в точку, оставаясь в пределах области.
Признак полного дифференциала содержится в следующей теореме.
Теорема 4. Пусть функции P(x,y), Q(x,y) имеют непрерывные частные производные до
второго порядка включительно в каждой точке односвязной области E. Тогда Pdx+Qdy – полный дифференциал Û 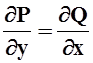 .
.
Доказательство. « Þ ». Если
Pdx+Qdy=dU=![]() dx+
dx+![]() dy,
то P=
dy,
то P=![]() ,Q=
,Q=![]() . А значит
. А значит 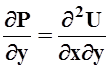 ,
,  .
По теореме о равенстве смешанных частных производных (теорема 14 из 9.4.3)
.
По теореме о равенстве смешанных частных производных (теорема 14 из 9.4.3) 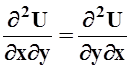 . Значит,
. Значит, 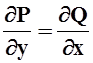 .
.
« Ü
». Пусть L – замкнутый
контур, лежащий в E.
Так как область односвязная, то L
является границей для области ELÍE.
Воспользуемся теоремой Грина: ![]() Pdx+Qdy=
Pdx+Qdy=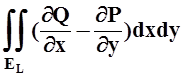 . Из
условия следует, что интеграл в правой части равен нулю. Значит,
. Из
условия следует, что интеграл в правой части равен нулю. Значит, ![]() Pdx+Qdy= 0. Так как это верно для любого замкнутого
контура L, то теоремы 3
и 2 показывают, что Pdx+Qdy
– полный дифференциал.
Pdx+Qdy= 0. Так как это верно для любого замкнутого
контура L, то теоремы 3
и 2 показывают, что Pdx+Qdy
– полный дифференциал.
Следствие. При указанных
предположениях о функциях P(x,y),Q(x,y) поле P![]() +Q
+Q![]() является потенциальным
тогда и только тогда, когда
является потенциальным
тогда и только тогда, когда 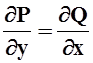 .
.
Если область не односвязная, то признак полного дифференциала перестаёт быть справедливым.
Пример 4. Рассмотрим интеграл 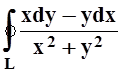 , где L – окружность
произвольного радиуса R
с центром в точке (0, 0). Здесь P(x,y) =
, где L – окружность
произвольного радиуса R
с центром в точке (0, 0). Здесь P(x,y) =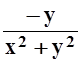 , Q(x,y) =
, Q(x,y) =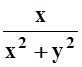 .
Условие
.
Условие 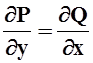 выполнено:
выполнено:
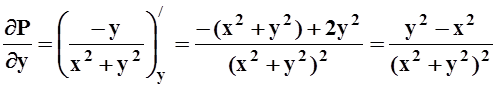 ,
,
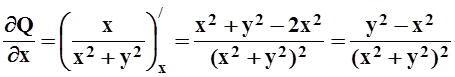 .
.
Однако полным дифференциалом (в области, где лежит окружность L) подинтегральное выражение не является, так как интеграл не равен нулю. Вычислим его, задавая окружность L параметрически:
x(t) = R cos t, y(t) = R sin t, t Î [0, 2p].
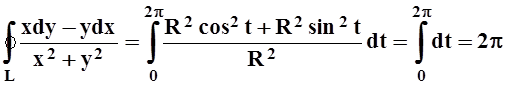 .
.
Причина здесь в том, что в точке (0, 0) функции P(x,y), Q(x,y) терпят разрыв. Если же эту точку удалить, то область, где лежат все такие окружности, перестаёт быть односвязной. Этот же интеграл по любой замкнутой кривой, не охватывающей точку (0, 0), равен 0.
12.1.5
Нахождение потенциала. Итак, мы научились определять, является ли
выражение Pdx+Qdy
полным дифференциалом (или, что то же самое, является ли векторное полеP![]() +Q
+Q![]() потенциальным). Теперь
научимся находить потенциал U(x,y) (т.е. функцию, для которой dU=Pdx+Qdy). Доказывая теорему 2, мы
видели, что в качестве такой функции можно взять
потенциальным). Теперь
научимся находить потенциал U(x,y) (т.е. функцию, для которой dU=Pdx+Qdy). Доказывая теорему 2, мы
видели, что в качестве такой функции можно взять
U(x,y) =![]() Pdx+Qdy,
(*)
Pdx+Qdy,
(*)
где (x0,y0) – произвольная точка (в области, где функции P(x,y), Q(x,y) обладают необходимыми свойствами), а интегрирование проводится по любому пути – результат от
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.