Теорема 13.Пусть функции u(x), v(x) дифференцируемы в точке x0 (напомним: для функций 1–й переменной это означает существование конечной производной в данной точке). Пусть функция f(u, v) определена в некоторой окрестности точки (u(x0), v(x0)) и дифференцируема в этой точке. Тогда сложная функция f(u(x), v(x)) дифференцируема в точке x0, причём
![]() .
.
Доказательство.Дадим приращение Dx переменнойx. Тогда функции u(x), v(x) получат приращения
Du = u(x0+Dx)–u(x0),Dv = v(x0+Dx)–v(x0).
По условию f(u, v) дифференцируема в точке (u(x0), v(x0)), т. е.
![]() .
.
Разделим обе части равенства на Dx:
![]() .
.
Перейдём к пределу приDx®0:
![]() , что и требовалось. Предел каждого из последних двух
слагаемых равен 0, так как Du®0, Dv®0,
, что и требовалось. Предел каждого из последних двух
слагаемых равен 0, так как Du®0, Dv®0,  ,
а пределы отношений
,
а пределы отношений ![]() ,
, ![]() существуют
и конечны.
существуют
и конечны.
Замечание.Теорема о дифференцировании сложной функции сформулирована и доказана в частном случае. Однако в других случаях правило дифференцирования аналогично. Например, пусть f = f(u, v, w), где каждая из функций u, v, w зависит от 2–х переменных: u = u(x, y), v = v(x, y), w = w(x, y). Тогда сложная функция f(u(x,y), v(x,y), w(x,y)) зависит от 2–х переменных. Её частные производные вычисляются по формулам, аналогичным выведенной в теореме 13:
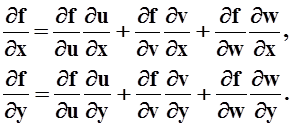
Рассмотрим свойства дифференциала, полезные при вычислении дифференциалов конкретных функций. Пусть u, v – дифференцируемые функции нескольких переменных; a, b, С – действительные числа.
1. dCº0;
2. d(au+ bv)= adu+ bdv;
3. d(uv)= udv+ vdu;
4.
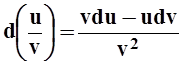 ;
;
5. Если f – дифференцируемая функция одной переменной, то
df(u)= f¢(u)du;
6. Если f – дифференцируемая функция двух переменных, то
![]() .
.
Докажем последнее свойство.
Пусть u = u(x, y), v = v(x, y). Так как 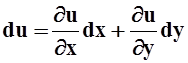 ,
, 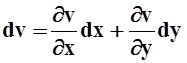 ,
то
,
то
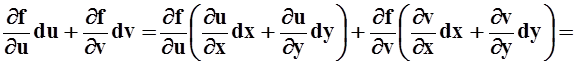

Полученное выражение, по определению, является дифференциалом df функции f(u(x,y), v(x,y)). Доказанное свойство называется инвариантностью формы полного дифференциала относительно выбора переменных. Дифференциал всегда равен сумме произведений частных производных на дифференциалы соответствующих переменных – и в случае независимых переменных, и в случае, когда эти переменные сами являются функциями.
Остальные свойства доказываются по одной схеме. Для независимых переменных – непосредственно из определения. Например, для 4 свойства:
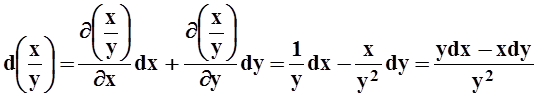 .
.
В общем случае, для функций u, v, справедливость свойства следует из инвариантности формы дифференциала.
Пример 8.Найти дифференциал функции f(x, y, z) = arctg(xz + y) в точке P(1, 1, 2).
Решение.Пользуемся свойствами дифференциала:

Дифференциал вычислен в произвольной точке. В точке P(1, 1, 2) он равен
![]() .
.
Замечание.Обратите внимание – вычисляя дифференциал, мы одновременно вычисляем и все частные производные. Например, из последней формулы видим: в точке P
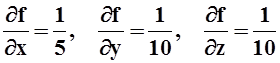 .
.
9.4.3 Частные производные и дифференциалы
высших порядков.Если не фиксировать, а менять точку, в которой
вычисляются частные производные, то они сами являются функциями, и их снова
можно дифференцировать. Например, если f = f(x, y), то частные производные 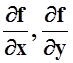 являются тоже функциями 2–х
переменных. Дифференцируя их, получим частные производные второго порядка:
являются тоже функциями 2–х
переменных. Дифференцируя их, получим частные производные второго порядка:

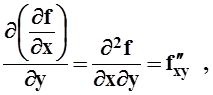
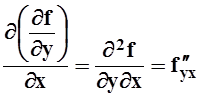 ,
,
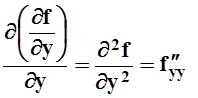 .
.
Запись ![]() читается «дэ
два эф по дэ икс дважды». Продолжая дифференцирование, можно определить частные
производные и более высоких порядков. Обозначения для них аналогичны. Если
дифференцирование проводится по различным переменным, то такие частные
производные называются смешанными. Например,
читается «дэ
два эф по дэ икс дважды». Продолжая дифференцирование, можно определить частные
производные и более высоких порядков. Обозначения для них аналогичны. Если
дифференцирование проводится по различным переменным, то такие частные
производные называются смешанными. Например, 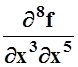 – одна из возможных смешанных
частных производных 8 порядка.
– одна из возможных смешанных
частных производных 8 порядка.
Пример 9.Найти частные производные 2 порядка функции f(x,y) = (x3+l)lny.
Решение.Находим сначала частные производные 1–го порядка:
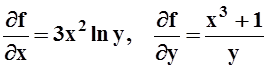 .
.
Теперь, дифференцируя далее, находим частные производные второго порядка:
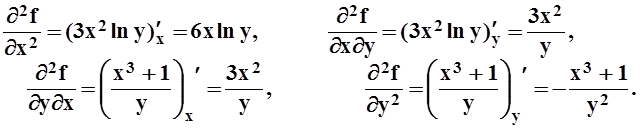
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.