 Теперь
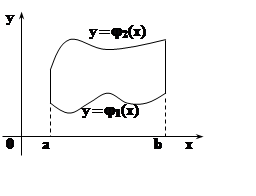
перейдём от прямоугольника к так называемым правильным областям. Множество
точек Е на плоскости,
ограниченное кусочно–гладкой кривой, называется правильным в
направлении оси OY, если любая
прямая, проведённая через внутреннюю точку множества параллельно этой оси,
пересекает её границу в двух точках. Из определения следует, что существуют
функции y= j1(x), y= j2(x)
такие, что
Теперь
перейдём от прямоугольника к так называемым правильным областям. Множество
точек Е на плоскости,
ограниченное кусочно–гладкой кривой, называется правильным в
направлении оси OY, если любая
прямая, проведённая через внутреннюю точку множества параллельно этой оси,
пересекает её границу в двух точках. Из определения следует, что существуют
функции y= j1(x), y= j2(x)
такие, что
E= {(x, y)ça£x£b,j1(x) £y£j2(x)}.
Двойной интеграл по области такого вида также можно вычислить с помощью повторного.
Теорема 6. Если f(x, y) непрерывна на указанной области E, то
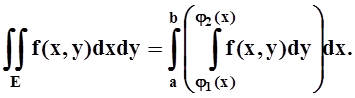
Доказательство теоремы 6 мы не приводим.
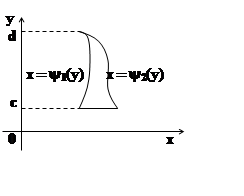 Обратим
внимание: внешний интеграл (тот, который вычисляется в последнюю
очередь) всегда имеет постоянные пределы. Отрезок [a, b] – это проекция E
на ось OX. Если область является
правильной в направлении оси OX,
то справедлива аналогичная формула:
Обратим
внимание: внешний интеграл (тот, который вычисляется в последнюю
очередь) всегда имеет постоянные пределы. Отрезок [a, b] – это проекция E
на ось OX. Если область является
правильной в направлении оси OX,
то справедлива аналогичная формула:
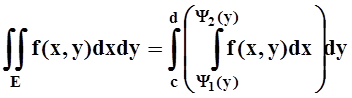 .
.
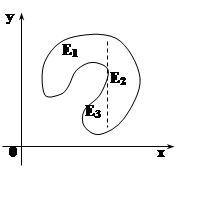 Если область имеет более сложную
структуру, то её нужно представить в виде объединения правильных областей и
воспользоваться свойством аддитивности интеграла. На рисунке:
Если область имеет более сложную
структуру, то её нужно представить в виде объединения правильных областей и
воспользоваться свойством аддитивности интеграла. На рисунке:
E= E1ÈE2ÈE3, 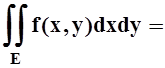
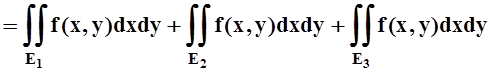 .
.
Пример
1. Вычислить 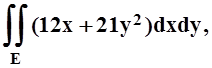 если область Е ограничена линиями y = 2x, y = x2 .
если область Е ограничена линиями y = 2x, y = x2 .
 Решение.
Сделаем чертёж. Область Е является
правильной в направлении любой оси, поэтому порядок интегрирования может быть
любым. Будем, например, интегрировать сначала по y, а потом по x:
Решение.
Сделаем чертёж. Область Е является
правильной в направлении любой оси, поэтому порядок интегрирования может быть
любым. Будем, например, интегрировать сначала по y, а потом по x:
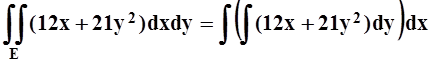 .
.
![]() Теперь
нужно расставить пределы интегрирования. Внешний интеграл (по х) имеет постоянные пределы. Находим их:
проецируя Е на ось OX,
получаем отрезок [0, 2]. Чтобы найти пределы внутреннего
интеграла (по y) «прокалываем» Е в направлении 0Y
лучом. Видим, что y изменяется от параболы (на ней y= x2) до
прямой (на ней y= 2x). После расстановки пределов интеграл
легко вычисляется:
Теперь
нужно расставить пределы интегрирования. Внешний интеграл (по х) имеет постоянные пределы. Находим их:
проецируя Е на ось OX,
получаем отрезок [0, 2]. Чтобы найти пределы внутреннего
интеграла (по y) «прокалываем» Е в направлении 0Y
лучом. Видим, что y изменяется от параболы (на ней y= x2) до
прямой (на ней y= 2x). После расстановки пределов интеграл
легко вычисляется:
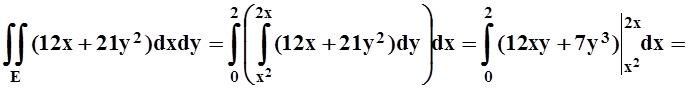
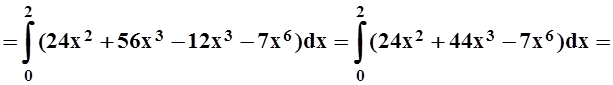
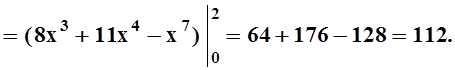
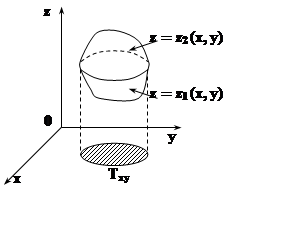 Вычисление
тройных интегралов проводится по аналогичной схеме. Пусть тело Т является правильным в направлении оси OZ , т.е. прямая, проведённая через любую
его внутреннюю точку параллельно OZ, пересекает
границу Т в двух точках. Тогда
Вычисление
тройных интегралов проводится по аналогичной схеме. Пусть тело Т является правильным в направлении оси OZ , т.е. прямая, проведённая через любую
его внутреннюю точку параллельно OZ, пересекает
границу Т в двух точках. Тогда
T={(x, y, z) | (x, y)ÎTxy, z1(x,y)£ z£ z2(x,y)}, где Txy – проекция Tна плоскость XOY, z= z1(x, y), z= z2(x, y)– уравнения поверхностей, ограничивающих T снизу и сверху. В этом случае
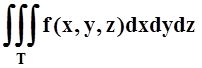
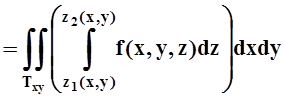 .
.
Подробнее: для вычисления тройного интеграла по указанной формуле необходимо:
1) найти проекцию Txy;
2) найти уравнения поверхностей, ограничивающих Tснизу: z= z1(x,y) и сверху z= z2(x,y);
3) вычислить внутренний интеграл, считая x, y постоянными и применяя формулу Ньютона–Лейбница;
4) вычислить двойной интеграл от полученного выражения по плоской области Txy. Если же тело T удобнее проецировать на координатную плоскость XOZ или YOZ, то формулы (и порядок действий) аналогичны:
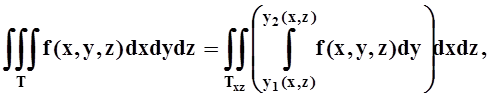
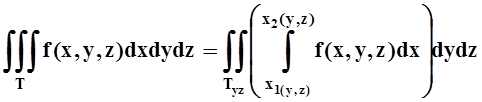 .
.
 Пример
2. Вычислить
Пример
2. Вычислить 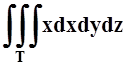 , если
тело Tограничено
поверхностями y= 1, y= x, x–2y= 0, z= x2+y2.
, если
тело Tограничено
поверхностями y= 1, y= x, x–2y= 0, z= x2+y2.
 Решение.
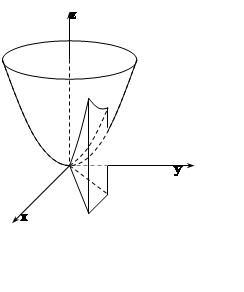
Сделаем чертёж. Поверхности y= 1, y= x, x–2y= 0 являются плоскостями,
параллельными оси OZ, они образуют
«вертикальные стенки» тела T.
Плоскость z = 0 определяет «дно» T.
Сверху тело T ограничено «крышей»
– параболоидом вращения z = x2+y2.
Решение.
Сделаем чертёж. Поверхности y= 1, y= x, x–2y= 0 являются плоскостями,
параллельными оси OZ, они образуют
«вертикальные стенки» тела T.
Плоскость z = 0 определяет «дно» T.
Сверху тело T ограничено «крышей»
– параболоидом вращения z = x2+y2.
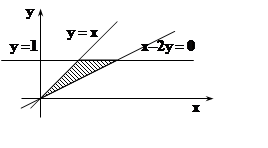
Будем проецировать T на XOY. Проекцией является треугольник Txy, изображённый на рисунке. Для определения пределов изменения Z, «прокалываем» T лучом, параллельным OZ. Луч входит через основание z= 0, выходит через «крышу» z = x2+y2. Поэтому
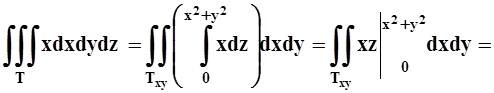
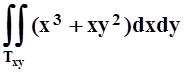 .
.
Вычисляем полученный двойной интеграл, интегрируя сначала по x, а затем по y:
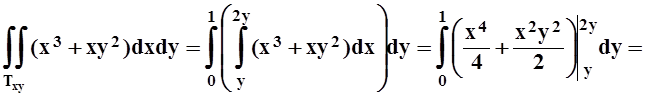
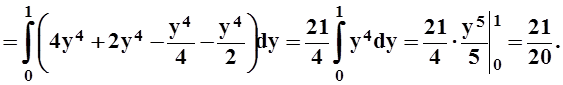
11.2.3
Замена переменных в кратных интегралах. Рассмотрим подробно случай
двойного интеграла. Пусть функция f(x,y) непрерывна на замкнутом измеримом
множестве Е. Тогда существует 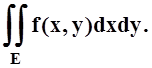 Пусть функции
Пусть функции
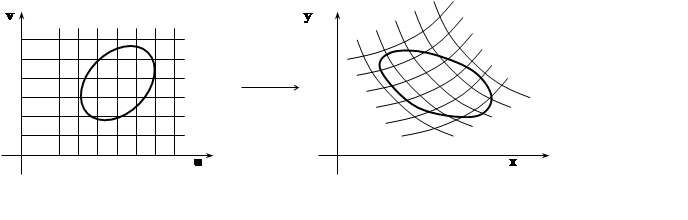
x = x(u, v), y = y(u, v)
задают взаимно–однозначное
отображение множества Е¢(на плоскости изменения переменных u, v )
на множество Е. Другими
словами, каждой точке (u, v)ÎЕ¢ взаимно–однозначно соответствует точка (x,y)ÎЕ. Пусть частные производные ![]() непрерывны на Е¢.
непрерывны на Е¢.
Теорема 7. При указанных предположениях справедлива формула
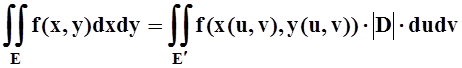 , где
, где 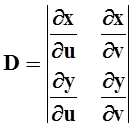 –
якобиан замены переменных.
–
якобиан замены переменных.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.