Марковская модель защиты информации при заданных ограничениях. Уровни защищенности информации при использовании различных моделей, страница 4

4) вероятность не преодоления с k  попыток

Р^(к)_{н пр} = 1 - Р⁽¹⁾_пр ;                                                          (2.12)

где Р_пр (Р_{н пр} ) - соответственно  вероятность попадания ( не попадания) на очаговую преграду.

Пусть в ИС установлено десять каналов утечки информации ( n = 10), четыре из них защищены однородными защитными механизмами ( m  =  4) с вероятностью преодоления с одной попытки Р_п⁽¹⁾ = 0,7.

Необходимо найти вероятность не преодоления системы защиты с  трех попыток - Р_нпр^(з).

1.  ;

Р_{н пп} = 1 - Р_пп = 0,6

2.

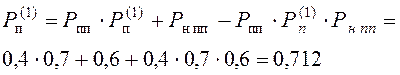
3.  Р_пр⁽³⁾ = 1 - (1 - Р_пр⁽¹⁾)³ = 1 - 0,288 ³ = 0,976

4.  Р_{н пр}⁽³⁾ = 1 - Р_пр⁽³⁾ = 1 - 0,976 = 0,024                                                          (2.13)

Серьезным недостатком всех рассмотренных моделей является то, что в них не учитывается тот факт, характерный практически для всех систем защиты, что злоумышленник может перейти к вскрытию очередного эшелона защиты только после того, как ему удалось преодолеть предыдущий.

Для устранения этого недостатка в данной работе разработан ряд моделей, базирующихся на математическом аппарате конечных марковских цепей, которые могут быть использованы на том или ином уровне исследования.

2.1.2  Аналитические ( марковские ) модели воздействия нарушителя

Вариант 1. Простая марковская модель защиты информации.

При разработке модели использованы следующие ограничения:

1) средства защиты различных эшелонов не однородны,  попытки преодоления одного и того же средства независимы;

2)  преодоление очередного средства возможно только после преодоления предыдущего. Преодоленные средства защиты не восстанавливаются.

Из анализа физической сущности процесса преодоления такой системы  преград можно сделать вывод о том, что данный  процесс является вероятностным, имеет конечное число дискретных состояний (равное числу преград плюс единица),  время преодоления каждой из преград является случайной величиной, в общем случае распределенной по не известному ( не показательному ) закону, т.е. процесс с классической точки зрения не  является марковским.

В таких условиях нахождение вероятностно-временных характеристик преодоления системы преград требует привлечения математического аппарата общей теории СМО. Однако, для достижения поставленных в работе целей исследования без особого ущерба для полученных результатов, можно ввести следующие допущения:

1) все события в процессе преодоления преград совершаются в некоторые дискретные моменты времени, именуемые шагами;

2) на длительность шага ограничений не накладывается;

3) переход из одного состояния в другое возможен с определенной вероятностью.

4) вероятность перехода в состояние j  на шаге  i  зависит только от того, в каком состоянии находится система на шаге (i - 1) и не зависит от того, каким образом она пришла в это состояние.

В таких предположениях можно исследуемый немарковсий процесс достаточно адекватно заменить вложенной в него конечной марковской цепью, для которой свойство марковости соблюдается только в моменты осуществления переходов из одного состояния в другое.

Тогда данный процесс может быть отображен графом состояний и переходов, изображенным на рис. 2.5 .

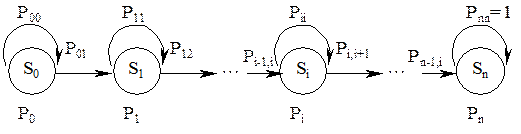
Рисунок 2.5-Граф состояний и переходов

Состояния, указанные на графе имеют следующее содержание:

S₀ - нарушитель осуществляет попытку преодоления внешней преграды;

S₁ - нарушитель преодолел внешнюю преграду и осуществляет попытку преодоления второй ( с внешней стороны) преграды;

S_i - нарушитель преодолел i - ую ( с внешней стороны ) преграду и осуществляет попытку преодоления  (i + 1) - ой преграды;

S_n - нарушитель преодолел последнюю (внутреннюю) преграду. Это событие является поглощающим. 

В качестве вероятностей перехода в графе, изображенном  на рис. 2.5, выступают вероятности преодоления (не преодоления) той или иной преграды (средства защиты).

Матрица переходных вероятностей для такого процесса примет вид:

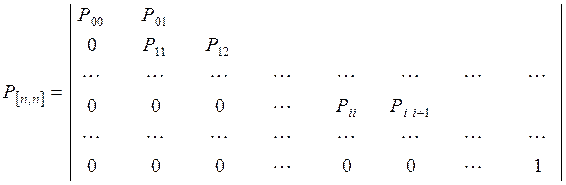       (2.14)

Ввероятность преодоления системы защиты за k  попыток будет определяться по уравнению Колмогорова - Чепмена

 ,                  (2.15)

где в качестве вектора исходного состояния принят вектор

P_<n+1>[0] = < 1 0 0 0 ... 0 >                                 (2.16)

Пусть модель системы защиты имеет вид, представленный на рис. 2.6.

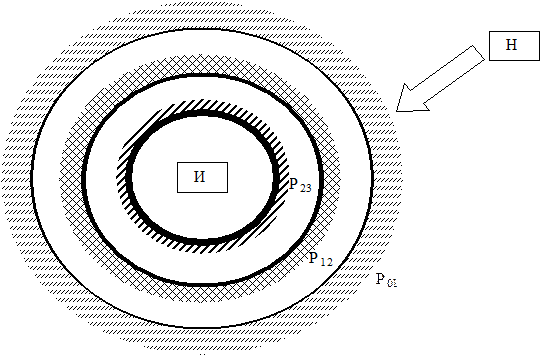
Рисунок 2.6 - Модель системы защиты