Суть двух критериев оценки устойчивости линейных ДСАУ и рекомендации по их использованию. Исследование переходных процессов ДСАУ в плоскости Z, страница 4

Проверите это на знаменателе (**) в примере 3. Убедились?!!!

2. Пусть разомкнутая система астатическая любой "ν" степени, и её ДПФ имеет такой вид:

,                                                                                (10. 8)

где А(z) и В(z) полиномы равные конечным числам при подстановке z=1, а второй сомножитель любой "ν" степени  интегратор.

_________________________________________________________________

⁴⁾ Эти следствия достаточно просты, но только второе я встретил в единственном известной мне источнике [29] из многочисленной литературы по теории ДСАУ. Поэтому считаю себя причастным к их разработке (С. Ковчин).

Тогда соблюдается следующее равенство между коэффициентами числителя и знаменателя замкнутой системы, представленной выражением (5. 8.):

                                                                                                                 (11. 8)

Это условие основано на том, что ДПФ замкнутой системы при z→1 равна единице.

Проверьте соблюдение условия (11. 8) в примере на формуле (*)!

3. Если разомкнутая система статическая, то в замкнутом виде её ДПФ будет также представлена выражением (5. 8). Но при z→1 из (5. 8) получаем следующее равенство:

                                     (12. 8)

где k – обобщенный коэффициент передачи разомкнутой системы.

Если учесть ,что в астатических системах , то второе следствие будет частным случаем третьего.

Итак, достоверность значений и знаков коэффициентов знаменателя выражения (6. 8) проверяется следствием 1, а достоверность значений и знаков коэффициентов его числителя проверяется следствием 3

6.5. Скрытые колебания в ДСАУ

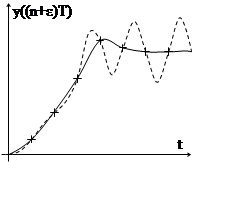
Представим, что некоторая дискретная система обладает следующим неприятным свойством: переходный процесс, представленный решетчатой функцией y[n,0] стремится к некоторому установившемуся значению. Однако переходный процесс представленный функцией y[n,0.5] таким стремлением не обладает (см. рис.2. 8).

Рис.2. 8.

Здесь, если построить огибающую кривую y_T(t) по точкам, обозначенным крестиками, то, вроде, можно заключить, что процесс сходится. Если же , учесть в огибающей ординаты y[n,0.5], расположенные между этими узлами (не показаны), то процесс получится расходящимся. Это может случиться, если линейная дискретная система неустойчива, период её колебаний равен двум периодам квантования и ординаты РФ y[n, 0] попадают в узлы этих колебаний.

В таких случаях говорят о наличии в системе "скрытых колебаний". Они могут появляться в системах, обладающих некоторыми специальными особенностями, а именно: содержащими колебательное звено.

Р. Горковенко. Насколько я понимаю, колебания в таком случае возникают именно из-за квантователя – импульсного элемента – он как бы раскачивает систему в резонанс с собой.

Изучением скрытых колебаний занимались многие ученые. Особо следует отметить исследования: Я. З. Цыпкина [4] (который и высказал предположение о необходимости наличия  в системе колебательного звена), С. М. Федорова [49], предложившего вариант расчетной формулы, Э. Джури [1] и Ю.Ту [16].

Отыскивать скрытые колебания в системе сложно. Мы этого коснемся при рассмотрении методов исследования ДСАУ в плоскости w, в следующих главах. Пока же отметим, что Я Цыпкин выдвинул следующее соображение: – колебательное (консервативное) звено, входящее в систему, не должно иметь собственную частоту колебаний "ν" кратную в целое число "n" половинной частоте квантования – ибо это вызовет резонанс, по-видимому, влекущий скрытые колебания. Если колебательное звено характеризуется, например, уравнением K(s)=kv²/(s²+2ξvs+v²) то следует следить за соблюдением неравенства: ω_КОЛ=v√(1–ξ²)≠nω_КВ/2.