Симметричные и несимметричные колебания в НСАУ
Исходные положения
При изучении проблемы устойчивости НСАУ было установлено, что устойчивость отдельных процессов может быть определена «в малом» или «в большом».
Для оценки устойчивости любых динамических процессов, то есть устойчивости не только отдельных процессов, но и самих систем применяют критерий абсолютной устойчивости. Но в НСАУ есть еще динамические процессы, которые обладают орбитальной устойчивостью.
Представим себе, что имеются динамические процессы, которые могут быть рассмотрены на фазовой плоскости. На этой плоскости можно изобразить некото-
|
|
рый
предельный цикл (см.
Если
возьмем какое-то начальное положение (xн.1,yн.1) внутри
этого цикла, то движение первого процесса (см. |
При других начальных условиях (xн.2,yн.2) движение
этого (второго) процесса (см. ![]() ) тоже будет затухающим, но перейдет на
орбиту и останется на ней.
) тоже будет затухающим, но перейдет на
орбиту и останется на ней.
|
|
При
уменьшении Ω увеличивается Т. Когда движение второго процесса
приходит на орбиту (см |
Общая теория симметричных автоколебаний
Рассмотрим
систему, состоящую из линейной и нелинейной частей. 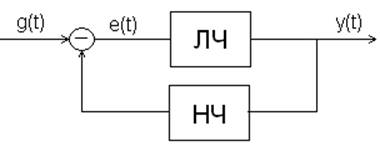 ЛЧ устойчива, а НЧ произвольного вида.
ЛЧ устойчива, а НЧ произвольного вида.
Используем
метод гармонической линеаризации для НЧ и получим характеристику Кнч(jA),
то есть комплексный коэффициент передачи НЧ: ![]() ,
,
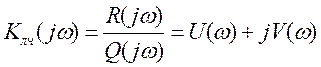 .
.
Составим частотную характеристику (оператор) замкнутой системы:
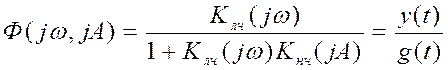 .
.
Перепишем
это выражение: ![]() .
.
При
наличии в системе автоколебаний, когда энергия не приходит извне, входной
сигнал g(t) = 0, а y(t) ≠ 0. Значит должно выполняться ![]() , называемое уравнением автоколебаний.
, называемое уравнением автоколебаний.
Откуда и получаем общую точку решения (необходимое условие автоколебаний):
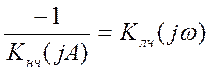 .
.
Построение точек решения с оценкой параметров автоколебаний
Обозначим 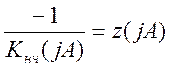 , тогда
, тогда 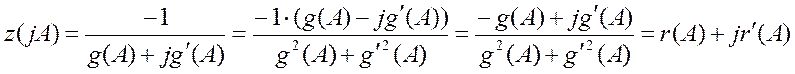 , где
, где 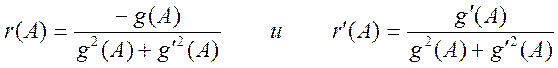 .
.
Следовательно, должно
выполняться ![]() .
.
Построим эти характеристики:
|
|
Пусть ЛЧ системы содержит два апериодических звена. Если
характеристика НЧ такова, что g' > 0 и g > 0 (релейная характеристика с опережающим
гистерезисом), тогда r(A) < 0 и r'(A) > 0, следовательно, z(jA)
расположена слева от K(jA) (см. |
Если характеристика НЧ есть отстающая релейная
характеристика, тогда
g' < 0 и g > 0, следовательно, Z2(jA) будет расположена в 3-м квадранте (см. ![]() ). Тогда появится два
решения (А1, Ω1) и (А2, Ω2). Но возникает вопрос: «А будут ли в этих точках автоколебания
устойчивыми?»
). Тогда появится два
решения (А1, Ω1) и (А2, Ω2). Но возникает вопрос: «А будут ли в этих точках автоколебания
устойчивыми?»
Оценка устойчивости состояния равновесия автоколебаний
Автоколебания в системе определяются выражениями ![]() и
и ![]() ,
следовательно,
,
следовательно, ![]() и
и ![]() .
.
Можно построить на фазовой плоскости эти процессы.
Исследуем на устойчивость орбиты 1 и 2. Из
операторного выражения 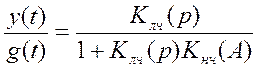 с учетом
с учетом 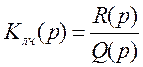 и
и 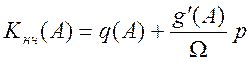 получаем:
получаем:
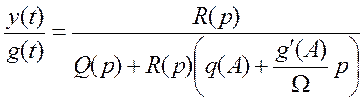 .
.
Операторное уравнение 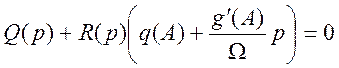 соответствует
точкам равновесия (орбитам) нелинейной системы, находящейся в режиме автоколебаний.
Полином
соответствует
точкам равновесия (орбитам) нелинейной системы, находящейся в режиме автоколебаний.
Полином ![]() ,
,
|
|
полученный
после замены 1) Изменим амплитуду А1:
Для устойчивости точки 1 необходимо, чтобы при частоте ω = Ω1 годограф Михайлова |
|
|
проходил через начало координат. От
точки равновесия при Если
амплитуду увеличить |
станет
неустойчивой (см. ![]() ).
Амплитуда колебание будет возрастать. Следовательно, точка 1 оказалась точкой (орбитой)
неустойчивого равновесия.
).
Амплитуда колебание будет возрастать. Следовательно, точка 1 оказалась точкой (орбитой)
неустойчивого равновесия.
|
|
2)
Рассмотрим точку А2. Дадим приращения амплитуде: При
|
При
малом изменении ![]() начало координат
начало координат ![]() переместится на плоскости
переместится на плоскости ![]() в направлении вектора r. Аналогично
переместится эта точка на вектор s, если
в направлении вектора r. Аналогично
переместится эта точка на вектор s, если
![]() .
.
|
|
Тогда
проекции векторов r и s на оси |
Угол
между векторами r и s будет определяться соотношением:
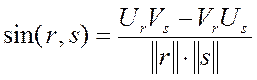 (получено из
(получено из ![]() . Пусть угол между векторами rи s находится в диапазоне от 00 до 1800,
. Пусть угол между векторами rи s находится в диапазоне от 00 до 1800, ![]() . Тогда
. Тогда 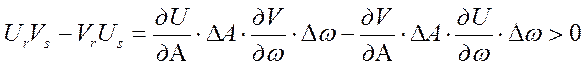 .
Если угол между векторами rи s находится в диапазоне от 1800 до 3600,
то
.
Если угол между векторами rи s находится в диапазоне от 1800 до 3600,
то ![]() . Тогда
. Тогда 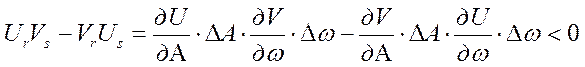 .
.
Откуда
при ![]() для
устойчивости режима автоколебаний необходимо и достаточно, чтобы:
для
устойчивости режима автоколебаний необходимо и достаточно, чтобы: 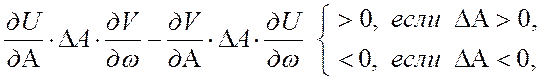 или:
или: 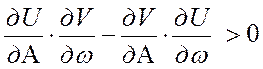 -
условие устойчивости колебательного режима, где частные производные
должны быть посчитаны в точке А и
-
условие устойчивости колебательного режима, где частные производные
должны быть посчитаны в точке А и ![]() .
.
Автоколебания в системах с однозначной нелинейностью
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.