Системы подчиненного управления (регулирования). Сравнительные характеристики параллельной и последовательной коррекций, страница 4

В системах подчиненного управления постоянные времени условно делятся на компенсируемые и не компенсируемые. Смысл компенсации вытекает из способности соответствующим образом настроенного регулятора ликвидировать (компенсировать) влияние апериодических звеньев. Большие постоянные времени подлежат обязательной компенсации. Часть малых также может быть скомпенсирована, но это не всегда бывает целесообразно (в случае постоянных фильтров), а другие не могут быть скомпенсированы, так как это - эквивалентные постоянные времени внутренних контуров, и их компенсация приведет к искажению, сбою настройки данных контуров.

Модульный оптимум

В силу того, что в реальных системах идеальной отработки входных воздействий добиться невозможно, то, как было отмечено ранее, в системах подчиненного управления пытаются обеспечить следующее качество амплитудно-частотной характеристики :

·  , то есть в области низких частот отработка сигналов идеальна,

·  отклонение  от единицы допустимо в области высоких частот:

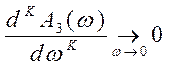,   К = 1, 2, 3, …

Настройка контура на модульный оптимум заключается в приведение его к звену второго порядка с определенными параметрами.

Передаточная функция замкнутой системы, настроенной на модульный оптимум, должна иметь вид:

;          .

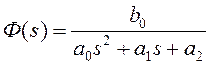Модуль частотной характеристики замкнутой системы

.

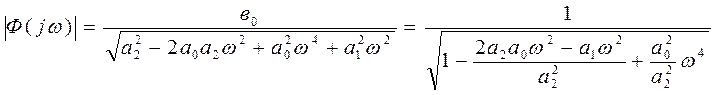Если положить ,  то  .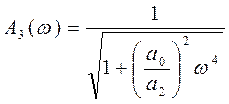

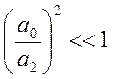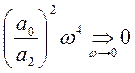Практически    ,  тогда        и   .

Условия  и  называются условиями приведения амплитудно-частотной характеристики системы к единице.

Амплитудно-частотная характеристика системы, настроенной на модульный оптимум, имеет вид:

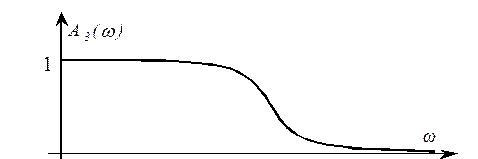
Передаточной функции замкнутой системы 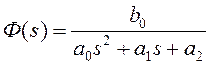 при условии  единичной  обратной связи и  соответствует передаточная функция

разомкнутой системы   . Тогда передаточная функция замкнутой системы будет записана как 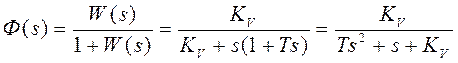. С учетом условия приведения амплитудной характеристики к единице  получаем: .  При этом соответствующие передаточные функции системы, настроенной на модульный оптимум, примут вид:

, 

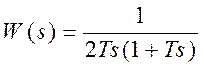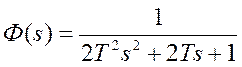
Следовательно, системе, настроенной на модульный оптимум, соответствует логарифмическая характеристика (ЛАХ разомкнутой системы типа 1 - 2):

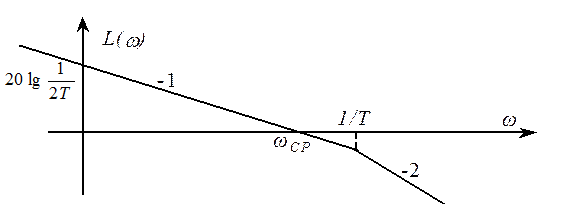
где    и 

и переходная характеристика (замкнутой системы):

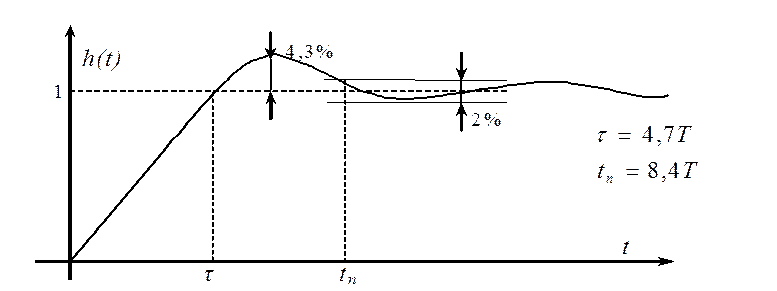
В силу того, что при настройке системы на модульный оптимум все большие постоянные времени объекта управления стараются скомпенсировать, а нескомпенсированными остаются только малые, то получаем:

,  ,  ,  .

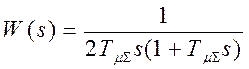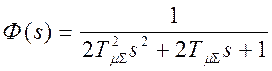Рассмотрим подробнее свойства колебательного звена:

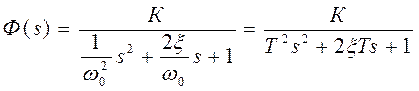,  , где ω₀ –частота собственных (недемпфированных) колебаний.  Если ξ = 0, то имеем консервативное звено. У реального звена коэффициент демпфирования находится в диапазоне:  .

Переходная характеристика колебательного звена определяется выражением:       ,  .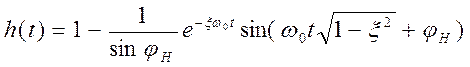

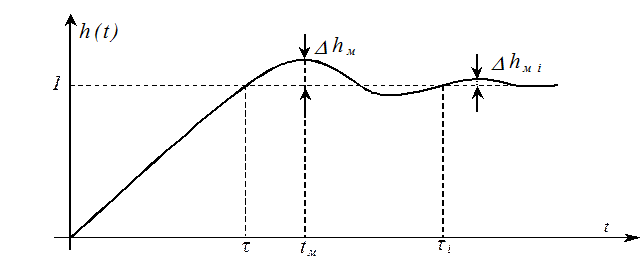
Из переходной характеристики получаем ее основные параметры:

перерегулирование  ,   ,

время  максимум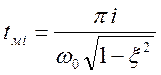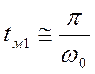а  ,   ,  отсюда , время согласования ,           .

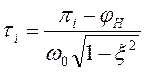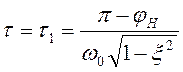ξ	σ %	w0 τ	w0 tм1
0.1	73%	1.68	3.16
0.5	16.3%	2.42	3.63
0.6	9.3%	2.77	3.94
	4.3%	3.33	4.44
0.8	1.5%	4.15	5.24
0.9	0.2%	6.19	7.22

Расчеты показывают, что наилучший случай наступает при ξ = ,что, как будет показано ниже, соответствует  настройке на модульный оптимум.

Примеры настройки на модульный оптимум

Выполним настройку на модульный оптимум контура с некоторыми разновидностями объекта управления.

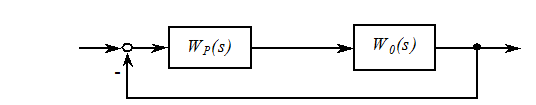
1.  Объект управления содержит малые инерционности: .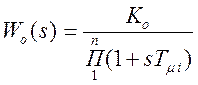

Выберем регулятор вида 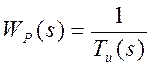    (потому что постоянные времени в передаточной функции объекта управления, подлежащие компенсации, отсутствуют).  Постоянная интегрирования регулятора подлежит определению:  Передаточная функция разомкнутой системы 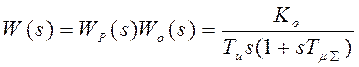, где 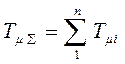(здесь выполнено эквивалентирование нескольких апериодических звеньев одним, потому что последовательно с ними расположен интегратор). Передаточная функция замкнутой системы

.

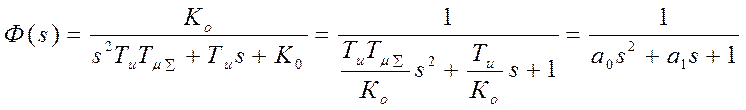Пусть выполняется условие приведения модуля частотной характеристики замкнутой системы к единице:  . Тогда 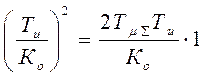, откуда и определяем искомое .