Синтез модального управления. Постановка задачи модального управления. Эталонная модель (коэффициенты характеристического уравнения системы), страница 2

Статическая точность однозначно определяется через коэффициенты g_i соответствующего характеристического полинома степени n.

Существует несколько форм эталонной модели.

1.  Модель в виде полинома Батнерверта.

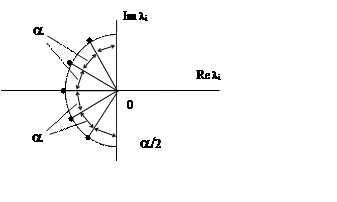Все корни характеристического полинома расположены в левой полуплоскости на одинаковом расстоянии от начала координат через равные углы.

 

Показатели:        s =15%

t_n 8,    где w₀ - радиус окружности (модуль корней).

K_ст =  - статический коэффициент (статическая точность).

n	j(s)
1	s + w0
2	s2 + 1,4w0s + w
3	s3 + 2w0s2 + 2ws + w
4	s4 + 2,6w0s3 + 3,4ws2 + 2,6ws + w
5	s5 + 3,24w0s4 + 5,24ws3 + 5,24ws2 + 3,24ws + w
6	s6 + 3,86w0s5 + 7,46ws4 + 9,13ws3 + 7,46ws2 + 3,86ws + w

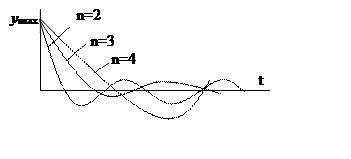
Переходный процесс в этом случае будет иметь вид:

 

2. Вторая форма записи коэффициентов – биномиальная форма.

Предполагается, что все корни – вещественные, отрицательные  и равные:

 

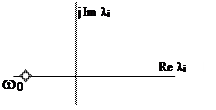j(s) = (s + w₀)ⁿ  - характеристический полином с желаемым распределением  (расположением) корней:

n	j(s)
1	s + w0
2	s2 + 2w0s + w
3	s3 + 3w0s2 + 3ws + w
4	s4 + 4w0s3 + 6ws2 + 4ws + w
5	s5 + 5w0s4 + 10ws3 + 10ws2 + 5ws + w
6	s6 + 6w0s5 + 15ws4 + 20ws3 + 15ws2 + 6ws + w

3. Третья форма коэффициентов характеристического полинома связана с минимумом интеграла от квадратичной ошибки:

e²(t)dt = (1 – y(t))²dt ;       y(0) = 1.

n	Характеристический полином
1	s + w0
2	s2 + w0s + w
3	s3 + w0s2 + 2ws + w
4	s4 + w0s3 + 3ws2  + 2ws + w
5	s5 + w0s4 + 4ws2 + 3ws2 + 3ws + w
6	s6 + w0s5 + 5ws4 + 4ws3 + 6ws2 + 3ws + w

Эта форма характеристического полинома обеспечивает большое быстродействие и большую колебательность системы.

4. Четвертая форма обеспечивает минимум интеграла от абсолютной ошибки.

|e(t)|dt   ®     min

n	j(s)
1	s + w0
2	s2 + 1,4w0s + w
3	s3 + 1,75w0s2 + 2,15ws + w
4	s4 + 2,1w0s3 + 3,4ws2 + 2,7ws + w

Таким образом, с помощью обратной связи по вектору состояния можно получить любую требуемую динамику замкнутой системы.

Пример. 

.                      Если  В_S 0,  то  имеется  внешнее  воздейy = Cx.                                       ствие (неавтономная система).

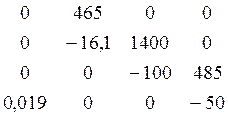
A = ;        B = ;        C = ();

Требование:                   t_n = 0,16 c;  s £ 15%;     K ³ 15 c^-1

Астатизм  I порядка      (добротность)

CF^-1 В_S = -E                              -условие, обеспечивающее статическую ошибку, равную нулю, при наличии возмущения.

F = A – BK                               - матрица замкнутой системы,

K – матрица обратной связи.

Синтез:

1)  Назначаем эталонную модель (первую форму):

j(s) = s⁴ + gs³ + gs² + gs + g

w₀ = = 50 с^-1;   g = 625*10^-4;   g = 325*10^-3;   g = 8500;   g = 130.

K_к =  = 19,2

2)  Можно проверить, что пара (A, B) – управляема.

3)  Найдем коэффициенты характеристического полинома матрицы А:

j(s) = det (sE – A) = s⁴ + as³ + as² + as + a = 0;

a = 603768, a = 80500, a = 7415, a = 166,1.

4)  Вычисляем матрицу М, преобразующую А к нормальной форме.

5)  Находим матрицу обратной связи  K_к = (212322; 244500; 1095; -36,1).

6)  Пересчитываем коэффициенты обратной связи  для исходной системы:     K = (0,16  2,5   –36,7  385).

7)  Управление  u = -0,16x- 2,5 x + 36,7 x - 385 x.

Наблюдатели

Система называется наблюдаемой, если по выходным параметрам и входным воздействиям можно определить ее вектор состояния.

Теорема. Необходимое и достаточное условие наблюдаемости:

rang(C^т | A^тC^т | C^т | … | C^т) = n.

Доказательство.