
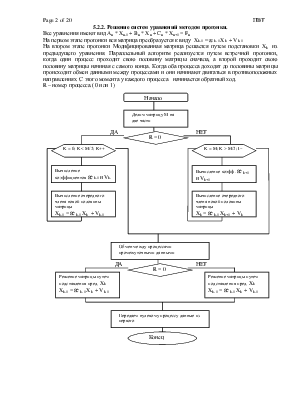





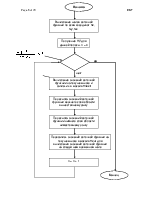

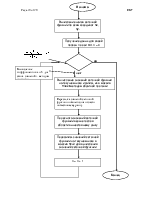


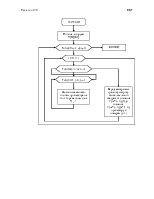



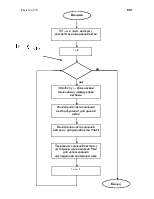



Когда оба процесса доходят до половины матрицы происходит обмен данными между процессами и они начинают двигаться в противоположных направлениях. С этого момента у каждого процесса начинается обратный ход.
R – номер процесса.( 0 или 1)
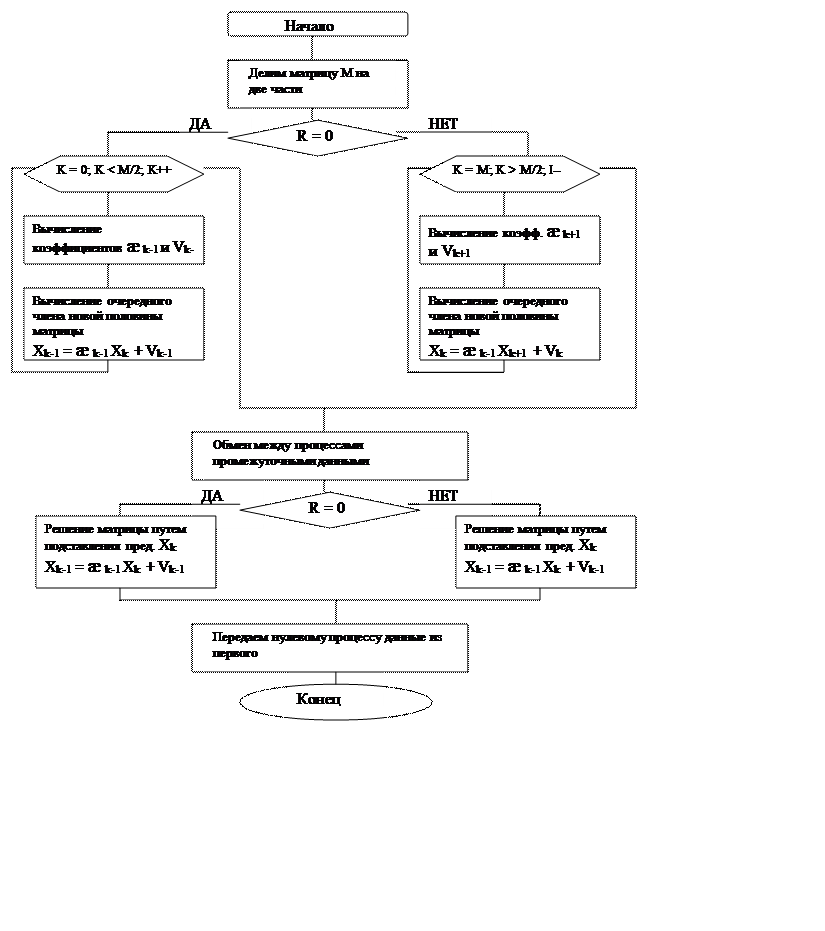
5.2.3. Решение системы линейных алгебраических уравнений методом Гаусса
|
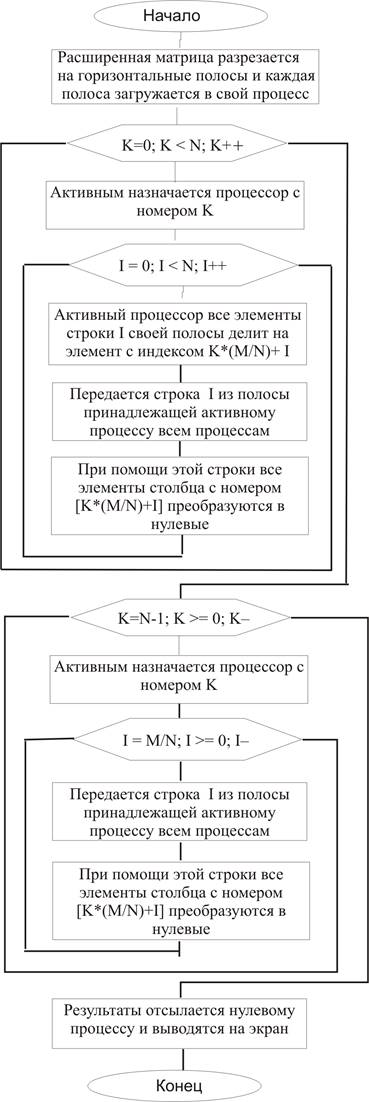
Раздел 5.2.4. Разностная схема продольно-поперечной прогонки
Двухшаговая разностная схема продольно-поперечной
прогонки порядка ![]() для
нелинейного уравнения (1) записывается в виде
для
нелинейного уравнения (1) записывается в виде
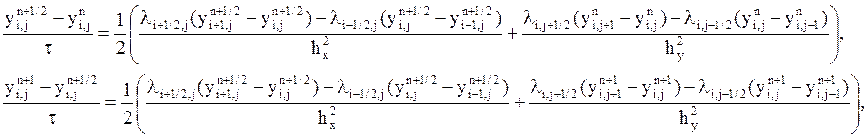 (3)
(3)
где: ![]() .
.
Такая разностная схема правильно аппроксимирует поток тепла, который является непрерывной функцией даже в том случае, когда коэффициенты уравнения (1) являются разрывными функциями.
По каждому из неявных направлений разностная схема по-прежнему является линейной и может быть записана в виде :
![]() (4)
(4)
где
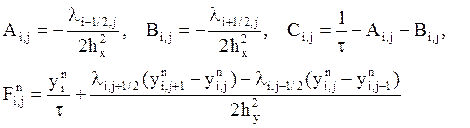
и соответственно
![]()
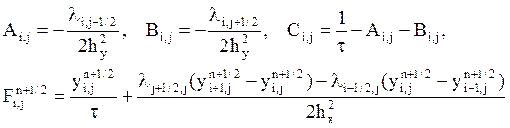
Для решения полученной системы линейных алгебраических уравнений используется метод прогонки.
Значения прогоночных коэффициентов находятся по рекуррентным формулам, которые в общем виде можно записать так:
![]() ,
k= 1, …, N-1. Из граничных
условий на левой (нижней) границах определяются значения прогоночных
коэффициентов
,
k= 1, …, N-1. Из граничных
условий на левой (нижней) границах определяются значения прогоночных
коэффициентов ![]() на
левой границе и
на
левой границе и ![]() на
верхней соответственно. После этого, учитывая, что
на
верхней соответственно. После этого, учитывая, что ![]() на
левой и
на
левой и ![]() на
правой границах, обратной прогонкой находятся все значения сеточной функции на
на
правой границах, обратной прогонкой находятся все значения сеточной функции на ![]() -
ом
-
ом ![]() n+1 –ом
n+1 –ом ![]() временном
слоях.
временном
слоях.
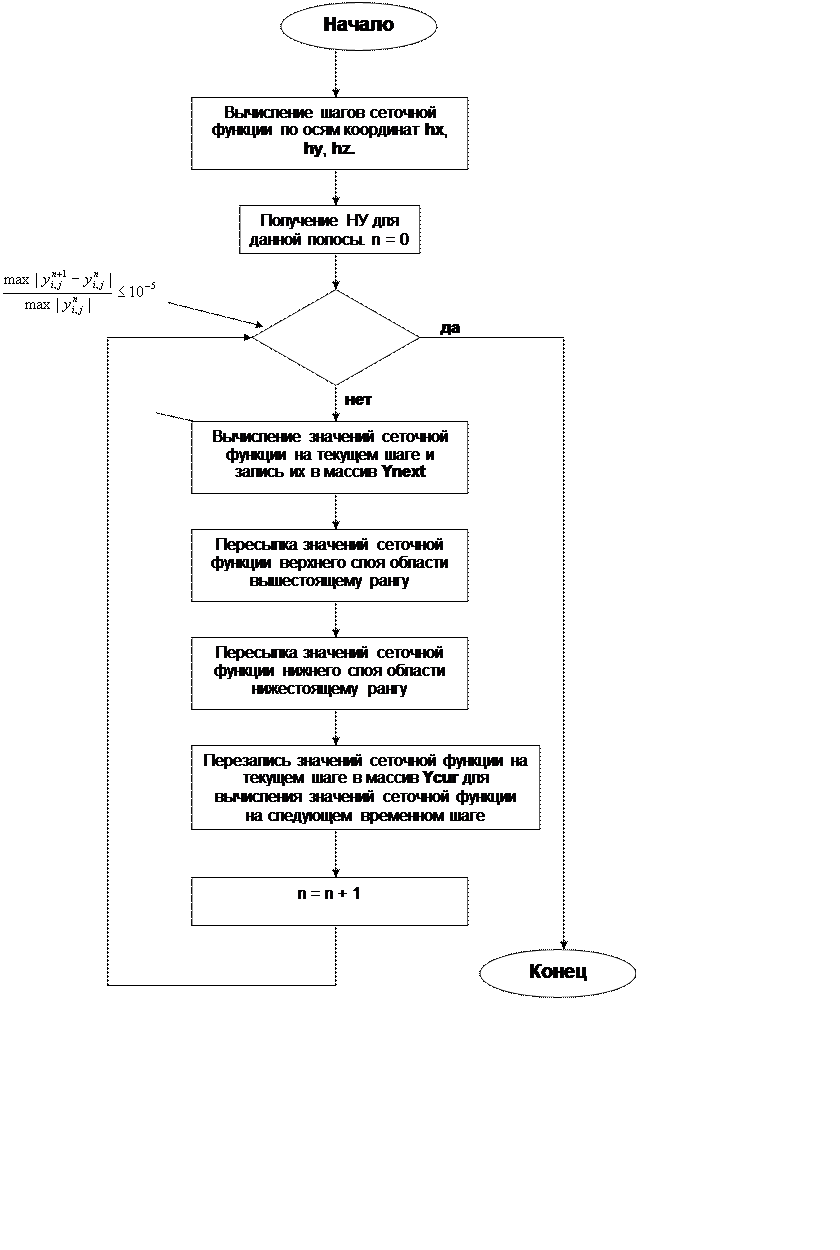
Блок схема алгоритма.
5.2.5
5.2.6. Написать блок-схему алгоритма распараллеливания для решения
двумерного уравнения Пуассона 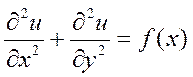 .
в области D{ 0 <= x
<= 1; 0 <= y <= 1; t > 0 } с помощью поточечного метода Зейделя (задача
Дирихле).
.
в области D{ 0 <= x
<= 1; 0 <= y <= 1; t > 0 } с помощью поточечного метода Зейделя (задача
Дирихле).
Поточечный метод Зейдея иногда называют итерационным методом и записывают разностную схему домноженную на hx2* hy2.
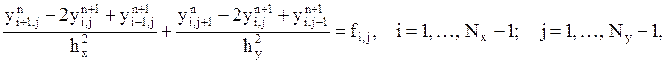
n – номер итерации.
Значения сеточной функции на границах области известно из граничных условий. Схему можно записать в виде, удобном для реализации ее с помощью бегущего счета:
![]() ,
где
,
где 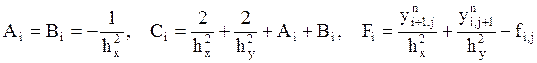 .
.
Значения ![]() находятся
по формуле
находятся
по формуле
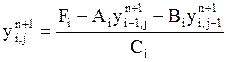 , причем счет начинается со значений индексов
, причем счет начинается со значений индексов ![]() .
В этом случае значение
.
В этом случае значение ![]() и
и
![]() известно
из граничных условий. В качестве начальных значений для внутренних точек
области можно взять, например, результаты линейной интерполяции между границами
и этими точками.
известно
из граничных условий. В качестве начальных значений для внутренних точек
области можно взять, например, результаты линейной интерполяции между границами
и этими точками.
Реализация алгоритма проста: разделяем ось OX на N частей, где N – количество параллельных ветвей. Какая-либо ветвь вычисляет значения функции для “своих” значений X, после этого передает верхний вычисленный слой ветви, с вышестоящим рангом, для того, чтобы на следующим шаге ветвь с вышестоящим рангом могла вычислить все свои значения функции. Также вышестоящая ветвь передает на каждом шаге нижний слой области нижестоящему рангу.

5.2.7.
Написать блок-схему алгоритма распараллеливания для решения двумерного
уравнения Пуассона 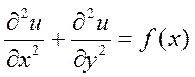 .
в области D{ 0 <= x
<= 1; 0 <= y <= 1; t > 0 } с помощью блочного метода
.
в области D{ 0 <= x
<= 1; 0 <= y <= 1; t > 0 } с помощью блочного метода
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.