Обратная задача теории упругости

Государственное образовательное учреждение
высшего профессионального образования

"ПЕТЕРБУРГСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
МИНИСТЕРСТВА ПУТЕЙ СООБЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ"
______________________________________________________________

А. В. Бенин          Н. И. Невзоров         И. И. Рыбина

		САНКТ-ПЕТЕРБУРГ 2007
	ОБРАТНАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ Методические указания

 

Бенин А.В., Невзоров Н.И., Рыбина И.И.

Представлены основные уравнения теории упругости, основные граничные задачи и способы их решения; варианты задания на выполнение расчетно-графической работы и примеры выполнения.

Для студентов строительных специальностей всех и форм обучения в ПГУПС.

Обратная задача теории упругости.

1.  Теоретические положения.

Основные уравнения теории упругости образуют три группы соотношений, отражающих статическую, геометрическую и физическую сторону задачи.

1.1. Статические уравнения.

К этой группе относятся дифференциальные уравнения равновесия (уравнения Навье)

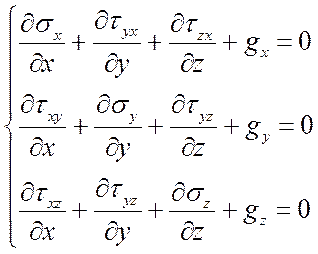                                                            (1)

и соотношения, выражающие свойство парности касательных напряжений

                                                     (2)

В эту же группу входят уравнения равновесия элементарного тетраэдра (формулы Коши):

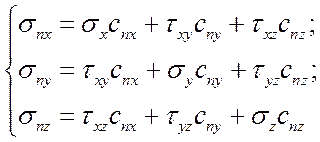                                                          (3)

при помощи которых можно определить проекции , ,  полного напряжения , действующего по наклонной площадке с нормалью , на оси декартовой системы координат. Если рассматриваемая площадка тетраэдра примыкает к поверхности тела, то в левой части (3) появляются проекции поверхностных сил, действующих на тело:

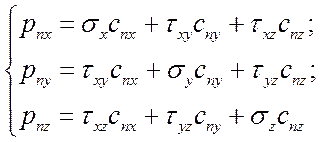                                                         (3^*)

В (3) и (3^*) через ,  и  обозначены направляющие косинусы нормали к площадке. В технической литературе для обозначения направляющих косинусов часто используют и другие обозначения:

;

;

.

Уравнения (3^*) используют для записи в напряжениях граничных условий (условий на поверхности тела), связывающих поверхностную нагрузку с напряжениями.

Важную роль (при постановке граничных условий, в технических дисциплинах, таких как сопротивление материалов) играют условия статической эквивалентности – интегральные зависимости между внутренними усилиями, действующими в поперечном сечении стержня, и напряжениями (рис. 1):

,    ,

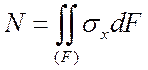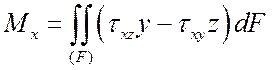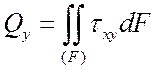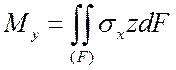,   ,                                                           (4)

,   .

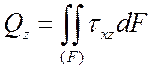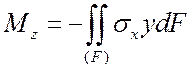Рис. 1

В этом примере ось x системы координат совпадает с осью стержня. Для того, чтобы записать условия статической эквивалентности в другой системе координат, достаточно произвести циклическую перестановку индексов в (4): .

В полную систему уравнений для решения задач теории упругости из статических соотношений входят три дифференциальных уравнения равновесия (1), содержащие шесть (с учетом свойства парности касательных напряжений) неизвестных.

1.2. Геометрические соотношения.

В этой группе в первую очередь следует выделить уравнения Коши, связывающие между собой упругие перемещения и относительные деформации:

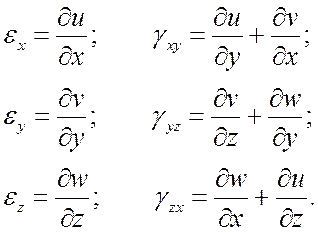                                                           (5)

При известных перемещениях u, v, w относительные деформации непосредственно определяются согласно (4). Задача нахождения перемещений по известным относительным деформациям существенно сложнее, поскольку для определения трех неизвестных функций имеется шесть уравнений (система переопределена). Необходимы дополнительные условия, обеспечивающие интегрируемость системы (4). Такими условиями являются уравнения Сен-Венана:

,             

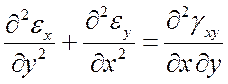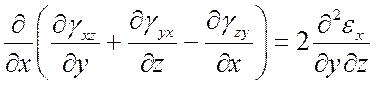
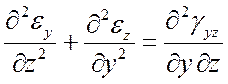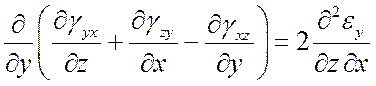,                       (6)

,              

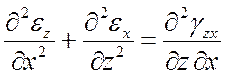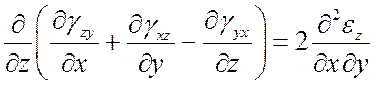
Физический смысл уравнений Сен-Венана – условие сплошности деформируемого тела; математический – условие интегрируемости уравнений Коши.

В полную систему уравнений теории упругости входят шесть уравнений Коши, содержащие шесть неизвестных.

1.3. Физические уравнения.

В линейной теории упругости, когда напряжения не превосходят предела пропорциональности, напряжения и деформации связывают между собой при помощи обобщенного закона Гука.

Прямая форма записи:

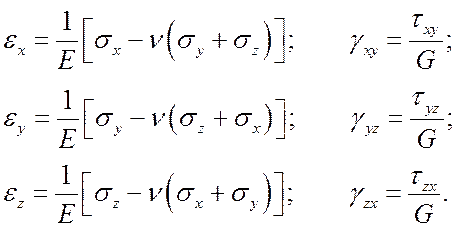                                   (7)

Здесь

-  E – модуль Юнга (модуль нормальной упругости, модуль упругости первого рода);

-  n - коэффициент Пуассона;

-  G – модуль упругости при сдвиге (модуль упругости второго рода).

Для однородного изотропного материала существует связь между этими упругими постоянными:

.

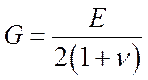Закон Гука в обратной форме:

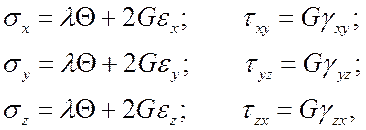                                               (8)

где

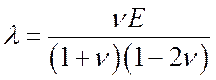-   - коэффициент Ламе;

-   - относительное изменение объема (объемная деформация).

1.4. Общая система уравнений теории упругости.
Прямая и обратная задачи.

Разрешающую систему уравнений теории упругости образуют:

-  дифференциальные уравнения равновесия (три уравнения, шесть неизвестных напряжений);

-  уравнения Коши (шесть уравнений, шесть неизвестных относительных деформаций и три неизвестных перемещения);

-  уравнения закона Гука (шесть уравнений).

Таким образом, для определения пятнадцати неизвестных имеется пятнадцать уравнений. Если одновременно используются все пятнадцать уравнений, не нужны уравнения совместности Сен-Венана, поскольку они непосредственно следуют из уравнений Коши. Найденные в результате интегрирования функции должны удовлетворять граничным условиям (3^*).

Принято различать два основных типа задач теории упругости.

1. Прямая задача. Заданы объемные и поверхностные силы. Требуется определить все упругие перемещение, напряжения и относительные деформации во всех точках рассматриваемого тела, включая его границу (поверхность).

Прямая задача теории упругости представляет наибольший практический интерес, однако ее решение чрезвычайно трудное из-за необходимости интегрировать сложную систему уравнений в частных производных и, главное, удовлетворять разнообразным граничным условиям.

В зависимости от вида граничных условий прямые задачи теории упругости подразделяют на следующие:

1)  первая основная задача – на границе тела заданы поверхностные силы;

2)  вторая основная задача – заданы перемещения точек поверхности тела;

3)  смешанная задача – на одной части поверхности заданы поверхностные силы, на остальной части – перемещения.

Обычно при решении прямой задачи полную систему уравнений теории упругости используют не непосредственно, а в преобразованном виде.

Наибольшее теоретическое и практическое развитие получили следующие два способа преобразования исходной системы уравнений.

1)  За основные неизвестные принимают упругие перемещения u, v, w. Относительные деформации записывают через перемещения по уравнениям Коши, результат подставляют в закон Гука, выражая тем самым напряжения через перемещения; в свою очередь полученные соотношения подставляют в уравнения Навье. Таким образом, решение задачи сводится к трем дифференциальным уравнениям, записанным относительно трех неизвестных перемещений. Такой метод называется решением в перемещениях.

2)  За основные неизвестные принимают шесть составляющих напряжений. Деформации выражают через напряжения при помощи закона Гука, результат подставляют в уравнения совместности Сен-Венана. Полученная система уравнений совместно с уравнениями Навье позволяет определить напряжения. Такой подход называется решением в напряжениях.

2. Обратная задача. Заданы функции, описывающие или упругие перемещения, или относительные деформации, или напряжения во всех точках рассматриваемого тела. Необходимо найти остальные неизвестные компоненты, в том числе объемные силы и условия на поверхности.

Решение обратной задачи всегда может быть получено, поскольку нет необходимости интегрировать сложную систему дифференциальных уравнений в частных производных, все сводится к простейшим математическим операциям.