Предмет исследования эконометрики. Задачи прогноза социально-экономических показателей, характеризующих состояние и развитие изучаемой системы

мера разброса зависимой переменной вокруг линии регрессии (необъясненная дисперсия);

 и  – стандартные отклонения коэффициентов  и , которые также называются стандартными ошибками;

 – средние значения изучаемых показателей.

Коэффициент b есть мера наклона линии регрессии. Очевидно, чем больше разброс значений y вокруг линии регрессии, тем больше ошибка в определении линий регрессии. Если  достаточно велика (регрессия оценена на достаточно широком диапазоне значений переменной x), то при данном уровне разброса ошибка в оценке величины наклона меньше, чем при малом диапазоне изменения объясняющего показателя.

Формально значимость оцененного коэффициента регрессии может быть проверена с помощью анализа его отношения к своему стандартному отклонению. Эта величина в случае выполнения условия Гаусса-Маркова имеет -распределение Стьюдента с  степенями свободы. Она называется -статистикой. В частности, для коэффициента  имеем

.                                      (15)

Для t-статистики проверяется нулевая гипотеза, т. е. гипотеза о равенстве ее нулю. Очевидно, что это равнозначно . Задается уровень значимости , число степеней свободы , и по приложению 1 находится . Если , то нулевая гипотеза не может быть отвергнута при заданном уровне значимости. Если , то с вероятностью  коэффициент модели регрессии значимо отличается от нуля.

Аналогично проверяется значимость коэффициента a с помощью t-статистики:

.                                     (16)

При оценке значимости коэффициентов линейной регрессии можно использовать нижеуказанное правило. Если стандартная ошибка коэффициента больше его модуля , то он не может быть признан значимым, поскольку доверительная вероятность здесь менее 0,7. Если , то оценка может рассматриваться как более или менее значимая . Значения  свидетельствуют о весьма значимой связи , при  – о практически достоверном ее наличии. Конечно, в каждом конкретном случае играет роль число наблюдений. Однако при  сформулированные правила действительны.

Интервальные оценки коэффициентов линейного уравнения регрессии определяются следующими доверительными интервалами:

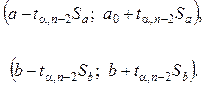                              (17)

17. Одной из основных задач экономического моделирования является прогнозирование значений зависимой (результативной) переменной при определенных значениях объясняющей (факторной) переменной.

Точный прогноз результативной переменной  в случае парной линейной модели регрессии рассчитывается по формуле

.                                    (18)

Точная оценка прогноза результативной переменной  с доверительной вероятностью  попадает в интервал прогноза, который оценивается по формуле

,                      (19)

где  – точечная оценка прогноза результативной переменной;

 – критическое значение критерия Стьюдента;

 – величина ошибки прогноза в точке k.

Величина ошибки прогноза в точке k рассчитывается по формуле

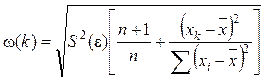,                          (20)

где  – несмещенная оценка дисперсии случайной ошибки линейной модели парной регрессии;

n – объем выборочной совокупности.

18. На исследуемый экономический показатель чаще всего оказывает влияние не один, а несколько факторов. Например, в макроэкономических исследованиях широко используется мультипликативная производственная функция, согласно которой валовой внутренний продукт зависит не только от капитала, но и от числа занятых в производстве рабочих. В этом случае вместо парной регрессии рассматривается множественная регрессия.

Задача оценки статистической взаимосвязи переменных Y и X₁, X₂, …, X_k формулируется аналогично случаю парной регрессии. Уравнение множественной регрессии может быть представлено в векторном виде следующим образом: , где  – вектор объясняющих переменных;

 – вектор подлежащих определению параметров;

 – случайная ошибка;   – объясняемая переменная.

Рассмотрим наиболее простую из моделей множественной регрессии – линейную. Она имеет вид ,  где  – зависимая переменная (предиктор);

,  – независимые переменные (регрессоры);

 – детерминированная составляющая (линейная функция независимых