Функции нескольких переменных. Понятие функции нескольких переменных. Предел функции. Частные производные и дифференциал функции

6. Прямые x = 1 и x = –1 являются ее вертикальными асимптотами. Выясним наличие наклонной асимптоты:

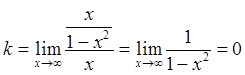( при  и при ),

.

Следовательно, есть горизонтальная асимптота, ее уравнение y = 0. Прямая y = 0 является асимптотой и при , и при .

График функции изображен на рисунке 6.

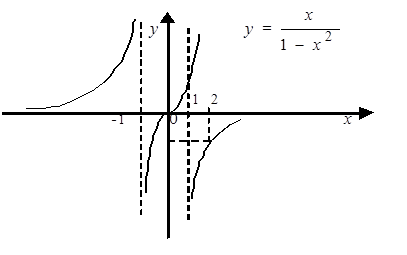
Рисунок 6

Ответы на тестовые задания

Номер теста	1	2	3	4	5	6	7	8
Правильный ответ	1	4	3	3	2	4	1	5

2.7. Функции нескольких переменных

Понятие функции нескольких переменных

Область определения

Переменная  называется функцией двух переменных x и y, если каждой паре (x; y) значений двух независимых друг от друга переменных величин x и y из некоторой области D соответствует определенное значение z: z = f(x; y).

Значение функции z = f(x; y) в точке M(x₀; y₀) обозначается z₀ = f(x₀; y₀) и называется частным значением функции.

Переменная величина  называется функцией трех переменных x, y, z, если каждому набору этих переменных соответствует единственное значение переменной u: u = f(x; y; z).

Будем пользоваться, заданием функции, как правило, аналитическим способом: когда функция задается с помощью формулы.

Множество всех точек, в которых определена функция n переменных, называется областью определения функции.

Область определения определяется из формулы функциональной зависимости путем соблюдения корректности выполнения соответствующих математических операций.

В случае двух переменных область определения функции z = f(x; y) представляет собой некоторое множество точек на координатной плоскости Oxyи тогда сама функция изображается в виде некоторой поверхности.

Пример 1. Найти  f(1; 2) для функции

Решение

Чтобы найти f(1; 2), надо в выражении для f(x; y) подставить x = 1, y = 2 и выполнить указанные в fдействия.

Имеем

Пример 2. Найти область определения функции и изобразить графически.

Решение

Эта функция двух переменных определена, когда выражение под знаком квадратного корня неотрицательно, т. е. 4 – х² – y² ³ 0 или x² + y² £ 4. Последнему соотношению удовлетворяют координаты всех точек, находящихся внутри круга радиусом R = 2 с центром в начале координат и на его границе. Область определения данной функции – указанный круг (рисунок 1).

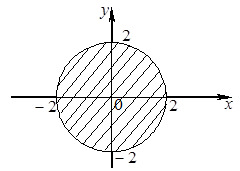
Рисунок 1

Пример 3. Найти область определения функции  и изобразить графически.

Решение

Данная функция определена на интервале [–1; 1], т.е.

 или   

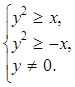
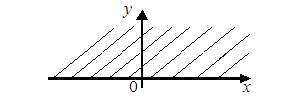
Неравенства y² ³ x и y² ³ – x задают часть плоскости, расположенную вне обеих парабол одновременно. Отметим, что точка (0; 0) не входит в искомую область определения.

Найденное множество точек, являющееся областью определения заданной функции, штриховкой показано на рисунке 2.

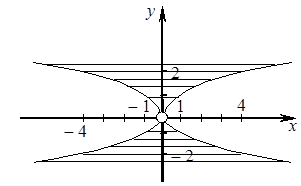
Рисунок 2

Пример 4. Найти область определения функции  и изобразить графически.

Решение

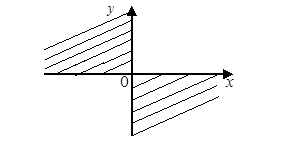
Область определения функции находится как решение неравенства:

 или .

Это неравенство описывает внутреннюю часть эллипса  (рисунок 3).

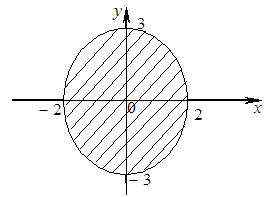
Рисунок 3

Тест 1. Значение функции  в точке (2; 1) равно:

1) 7;   

2) –5;

3) –1;

4) 1;

5) –2.

Тест 2. Область определения функции является:

1)

2)

3)

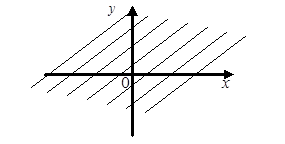
4)

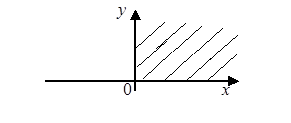
5)

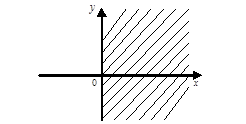
Тест 3. Указать функцию двух переменных:

1)

2)

3)

4)  

5)

Предел функции

Число  называется пределом функции z = f(x; y) в точке M₀(x₀; y₀), если для любого числа e > 0 найдется число d > 0 , зависящее от e, такое, что для всех точек M(x; y), отстоящих от M₀  не более чем на d, выполняется неравенство .

Записывают: .

На функции нескольких переменных легко переносятся все положения теории пределов функции одной переменной, в частности справедлива теорема.

Теорема

1) ;

2) ;

3) 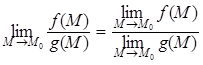, если .

Пример 5. Найти предел .

Решение

.

Пример 6.Найти предел .

Решение

Имеем неопределенность вида . Раскроем эту неопределенность. Избавимся от иррациональности в числителе:

.

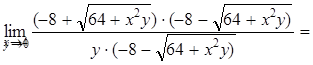
Пример 7. Вычислить .

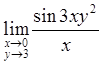Решение

Имеем неопределенность вида . Находим:

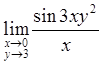
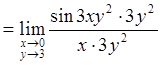
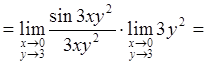
, так как

Пример 8. Вычислить .

Решение

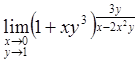Имеем неопределенность вида . Выражение, стоящее под знаком предела, преобразуем к такому виду, чтобы можно было воспользоваться вторым замечательным пределом:

.

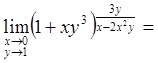
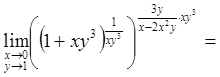
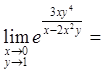
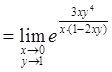
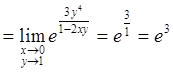Пример 9. Вычислить .

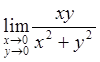Решение

Данная функция  определена всюду на координатной плоскости Oxy, кроме точки O(0; 0). Рассмотрим предел этой функции при стремлении точки M(x; y) к началу координат по любой прямой, проходящей через точку O, т.е. вдоль линии  :

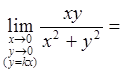
Получили, что значение предела зависит от углового коэффициента прямой. Итак, соответствующим разным значениям k получаем разные предельные