Математические модели сигналов. Динамическое представление сигналов (ДПС) с помощью функций включения и дельта-функций, страница 2

Изменение величины S(T) тем точнее, чем короче реальный сигнал, приблизительно представляющий дельта-функцию.

2. Существует два важнейших вопроса в теории сигналов:

1) Как можно сравнивать сигналы по величине? И что такое величина сигнала вообще?

2) Как объективно оценить на сколько два неодинаковых сигнала похожи друг на друга?

Ответ дает функциональный анализ, являющийся базой теоретическо-множественного представления сигналов в виде вектора в бесконечно мерном пространстве.

а) Линейное пространство сигналов:

пусть M={S₁, S₂, …} – некоторое множество сигналов, объединенных некоторым свойством.

Например: множество сигналов S_j=A_jcos(w_jt+φ_j).

Это означает, что множество сигналов наделено определенной структурой. Эта структура обусловлена физически: электрические колебания могут складываться, а также перемножаться на произвольную константу. Поэтому такой структурой может быть линейное пространство.

Аксиомы вещественного линейного пространства:

1) Любой сигнал U, который пренадлежит M, при любом времени принимает лишь вещественные значения.

2) Для любого U, который пренадлежит M и V, который пренадлежит M, существует их сумма W=U+V, причем W тоже пренадлежит M, при этом сумма коммутативна и ассоциативна: U+V=V+U, U+(V+X)=(U+V)+X.

3) Для любого сигнала S, пренадлежащего M и любого вещественного числа α определяет сигнал F= α*S.

4) Множество M содержит особый нулевой элемент Ø, такой что: U+ Ø =U, для любого U, пренадлежащего M.

Введение структуры линейного пространства – это первый шаг к геометрической трактовке сигналов. Сигнал, как и линейное пространство – вектор.

Далеко не всякое множество сигналов является линейным пространством.

Например: множество M прямоугольных импульсных напряжений на интервале [0; 20 мкс], причем амплитуды ≤ 10 В.

Ведь если сложить импульсы с амплитудами 6 и 8 В, то получим импульс, не содержащийся в множестве M и поэтому M не образует линейного пространства.

Понятие координатного базиса: совокупность векторов {е₁, е₂, …, е_n, …} пренадлежащих M является линейно независимым координатным базисом.

Если равенство

   возможно лишь в случае одновременного обращения в ноль всех коэффициентов .

Если сигнал S(t) задан в виде следующего выражения:

   , то числа {c₁, c₂, …} являются проекциями сигнала S(t) относительно выбранного базиса.

Если число базисных векторов велико, то такое линейное пространство бесконечно мерное.

Нормированное линейное пространство. Энергия сигналов.

Норма – длина вектора.

Нормированное – если любому S(t), пренадлежащему L, однозначно соответствует ||S||.

ЛПС:

1) Норма неотрицательна, причем норма равна нулю, если сигнал S=Ø.

2) Для любого α: ||αS||=|α|||S||.

3) Если вектора S(t) и P(t) пренадлежат L, то норма суммы менее или равна сумме норм.

Норма вещественного сигнала:

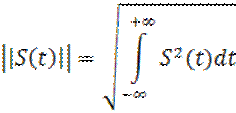                                                                                        (12)

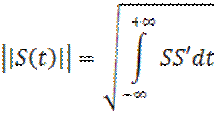                                                                                         (13)

S' – комплексно сопряженный сигнал к сигналу S.

Квадрат нормы - есть энергия сигнала.

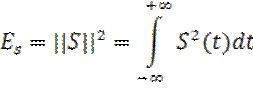                                                                                   (14)

Использовать понятия нормы целесообразно, потому что оно не чувствительно к изменению формы сигнала, пусть и значительным и кратковременным.

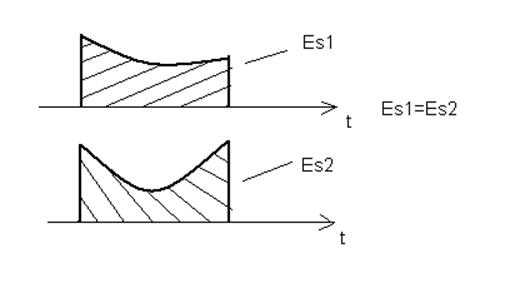
Рисунок 8

Метрическое пространство.

ЛПС L становится метрическим, если каждой паре сигналов U и V, пренадлежащих L, соответствует  число ρ(U,V)≥0, то это называется метрикой сигналов.

Аксиомы:

1) ρ(U,V)= ρ(V,U) – рефлексивность метрики.

2) ρ(U,V)=0, при V и U, пренадлежащих L.

3) Для любых w, пренадлежащих L, справедливо неравенство ρ(U,V)≤ ρ(U,W)+ ρ(W,V).

Метрика – норма разности двух сигналов:

ρ(U,V)=||U-V||                                                                                               (15)

Любая норма :

||U||=ρ(U,Ø).

Метрика позволяет судить  насколько точно позволяется аппроксимировать другой.